试论公有制企业高效率的充分条件

□徐跃华朱殊洋（、广州大学马克思主义学院，广东广州 50006；、中共广州市委党校经济学教研部，广东广州 50070）

试论公有制企业高效率的充分条件

□徐跃华1朱殊洋（21、广州大学马克思主义学院，广东广州 510006；2、中共广州市委党校经济学教研部，广东广州 510070）

市场经济条件下，如果公有制企业采取如下要素投入原则：是否追加生产要素取决于该生产要素是否能够带来纯收入增加，则公有制企业是高效率的。这就是公有制企业高效率的充分条件。

公有制；最优激励；全要素生产率；最优资源配置

习近平总书记在中央政治局第28次集体学习会议上强调，要坚持公有制主体地位不能动摇，国有经济主导作用不能动摇，这是保证我国各族人民共享发展成果的制度性保证，也是巩固党的执政地位、坚持我国社会主义制度的重要保证。为了保持公有制企业的主导地位，就需要提高它的效率。那么，如何提高公有制企业的效率呢？换句话说，公有制高效率的充分条件是什么？这不仅是一个重要的理论问题，也是一个重大的现实问题。本文试图在理论上对这一问题进行初步探索。

一、基本假设

（一）效率评价标准假设

效率高低主要取决于两个方面：一是生产方面，包括纯收入是否最大化，生产效率和资源配置效率状态；激励状态。二是消费方面，即消费者福利水平。

（二）劳动者追求公平假设与最优激励条件

企业内每个劳动者的积极性取决于每单位劳动投入所带来的价值收入与每单位劳动投入所创造的价值之差。如果每单位劳动所带来的价值收入大于每单位劳动所创造的价值，则劳动积极性上升；否则劳动积极性会下降。

根据马克思劳动价值论，价值由活劳动创造，而价值分配由生产资料所有权决定；价值的创造是基础，没有价值也就无所谓价值分配，价值分配又反作用于价值创造。用li、yii分别表示第i个劳动者所付出的劳动、新创造的价值收入和得到的价值收入，那么最有激励的条件是Ai，yi/li=/li。当每个劳动者都实现了yi/li=/li，则称之为最优相容性激励，简称最优激励。总之，只有企业每个劳动者的价值创造与价值分配达到了一致性，才能够实现最优激励。

（三）所有制的特征假设

在公有制下生产资料归社会所有，全部新创造的价值收入归于劳动。笔者用符号Y表示一定时期内企业得到的实际纯价值收入，L表示该时期的全部劳动投入，K表示该时期内全部资本存量。于是，公有制是全部劳动L得到Y，即Y/L。

（四）公有制要素投入原则

在市场经济条件下公有制企业要素投入原则：是否追加生产要素取决于该生产要素是否能够带来纯价值收入增加。将这一要素投入原则简写为“原则I”。

二、从生产角度的考察

（一）对纯收入最大化（即利润最大化）的考察

命题1：在原则I下，公有制企业可以实现纯收入最大化。

证明：首先来考察短期情况。可以证明从短期看，利润最大化与市场经济要素投入原则是等价的。事实上，由纯收入定义可知，Y=（L1gggLn）-rK-wL。在短期中K为常数，对该式分别求导数得到利润最大化条件∂Y/∂L1=w，…，∂y/∂Ln=w，，即∂Y1/∂L1=…=∂Y1/∂Ln。这恰恰是市场经济要素投入原则。反之，如果∂Y1/∂L1=…=∂Y1/∂Ln，则必有利润最大化。

再来考察长期情况。设企业生产函数为Y=Y（L，K），其中K、L皆为变量。根据市场经济要素投入原则得：做李雅普诺夫函数：V（t)=½（L-L*)2+½（K-K*)2，其中L*、K*为短期利润最大化情况下的最佳投入，则有：

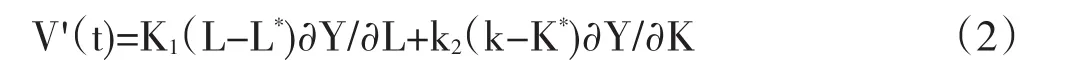
根据市场经济要素投入原则得（L-L*)∂Y≤0，（k-K*)∂Y/∂K≤0，于是可知V（'t)≤0，由此推知L=L*，K=K*是大范围稳定的。因而长期看企业收敛于利润最大化状态。证毕。

（二）对生产效率的考察

命题2：在原则I下，公有制企业可以实现生产效率最优。

证明：首先考察短期情况。短期内K不变，投入的活劳动为L=Li，Li为第i个劳动者投入的活劳动量。生产函数是Y=Y（L）。由于Y是由活劳动创造的，因此短期全要素生产率可以定义为A=Y/ L。为了简单而不失一般性，设企业只生产一种产品，则短期内全要素生产率最优条件是：∂Y/∂L1=∂Y/∂L2=…∂Y/∂Ln=Y/L。

公有制企业满足这一最优条件吗？答案是肯定的。事实上，前面已经证明，在市场经济要素投入原则下在公有制企业中存在∂Y/∂L1=∂Y/∂L2=…∂Y/∂Ln，结合公有制特征Y/L和命题1，即得∂Y/∂L1=∂Y/∂L2=…∂Y/∂Ln=Y/L，这就是生产效率最优的充分条件。

再来考察长期情况。在考察长期情况之前，首先需要给出长期全要素生产率的定义。现代经济学教科书中将长期全要素生产率定义为Bx=Y（K，L）/（K+L）。根据马克思劳动价值论，活劳动是价值的源泉，因此物化劳动的任何改变均来自于活劳动的改变。设K=K（L1），其中L1是改变K的活劳动。设生产消费资料的活劳动为L2，由此得到新价值生产函数Y=Y[K（L1），L2]。将其代入全要素生产率定义得：下面证明（3）式的等价形式是：

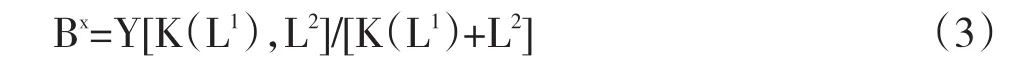
接下来笔者要证明全要素生产率（3）与（4）式是等价的。首先不妨证明（3）式⇒（4）式。因为与全要素生产率（3）相对应的长期生产函数为Y=Y[K（L1），L2]，所以可以得到进而有因为其代入上式得：

而（5）式表明新价值只是来自于两种活劳动，于是得到全要素生产率为（4）式。

再来证明（4）式⇒（3）式。由马克思劳动价值论可知，与（4）式相对应的长期生产函数为Y=Y（L1，L2），因此有。由K=K（L1）得，进而得到。将和

代入（5）式得

由（6）可知，其生产效率表示为（3）式。

有了前面的理论准备，就可以分析公有制与长期生产效率的关系了。做李雅普诺夫能量函数

其中βi为大于零的常数，L1*和L2*分别为短期内最优的生产生产资料的劳动和生产消费资料的劳动量。对该函数求导得V'（t）=β1（L1-L1*）（dL1/dt）+β2（L2-L2*）（dL2/dt）。根据市场经济要素投入原则可以得到，（L1-L1*）（dL1/dt）≤0，（L2-L2*）（dL2/dt）≤0，所以V'（t）≤0。证毕。

（三）对资源配置效率的考察

命题3：在原则I下，公有企业可以实现资源最优配置。

证明：首先考察的情况。不失一般性，这里只考察两种产品的情况。设L+K0=Ω。其中K=K0为物化劳动，短期看为常数；L为当期活劳动；Ω为总的劳动量。生产函数如前。做拉格朗日函数：

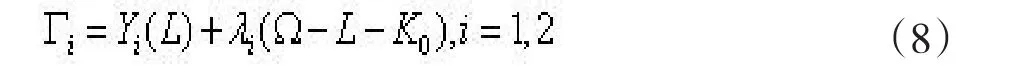
在市场经济要素投入原则下，由命题1可知纯收入最大化存在，则

结合（9）、（10）得（∂Y1/∂Li）/（∂Y1/∂Li）=（∂Y2/∂L1）（∂Y2/∂Li）。

再来考察长期下资源配置情况。可以肯定长期中公有制企业也能够实现最优。事实上，由命题1知在市场经济要素投入原则下存在利润最大化，而利润最大化是大范围稳定的，也即（9）和（10）式是大范围稳定的，因此（∂Y1/∂Li）/（∂Y1/∂Li）=（∂Y2/∂L1）（∂Y2/∂Li）也是大范围稳定的。证毕。

（四）对最优激励的考察

命题4：在原则I下，公有制企业可以实现激励最优。

证明：首先考察短期情况。由文献[1]（P80-83）得到短期马克思生产函数Y=AK1-αLα，其中α、A、K为常数，α为收入对劳动的弹性指标。根据马克思剩余价值论，纯收入均来自工人的活劳动，即收入只来自于工人的活劳动。令YLi表示第i个劳动对产出的贡献，则必有

其中YLiLi为第i个劳动者付出劳动量Li所创造的价值，则

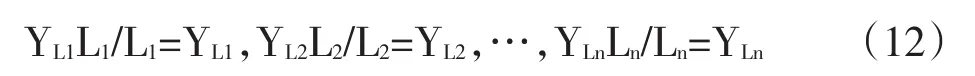
由生产效率最优条件得到

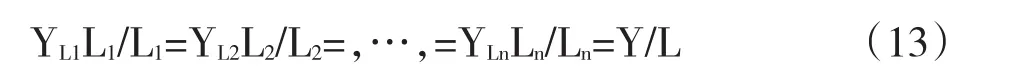
因为yi=YLiLi，所以上式为

由文献[1]（P80-83）可知，在短期内，马克思生产函数为Y=AL。因为总产出等于总收入，即Y=Y，所以AL，于是可以得到

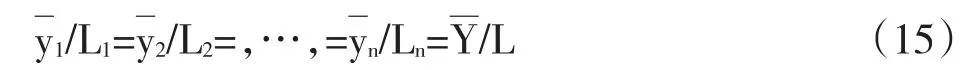
再来进行长期考察。设某一劳动者劳动投入的变化率为dLi/dt。由市场经济要素投入原则得

三、从消费角度的考察

设一个社会由一个企业组成，企业中有两部分人，一部分人消费第i种商品的数量表示为xi，另一部分人消费第i种商品数量表示为zi。总效用是两种人效用之和。商品集为N，集合中包含n个元素。

命题5：在原则I下，公有制企业可以实现消费者福利最大化。

证明：证明的思路是，先将企业看做是私有制企业，并考察其福利状态。然后考察在参数变化下的福利状态的改变，进而得到参数改变的极限状态恰恰就是公有制。不失一般性，这里只考察一个工人和一个资本家的消费者均衡问题，然后加总即可。笔者按着时间序列进行递推。

先考察第t期的情况。设第t期工人的效用函数为GU1=GU1（N），工资为y1，商品i的单价为ci，则预算条件为cixi=y1。资本家的效用函数为ZU2=ZU（2N），纯收入（利润）为y2，则预算条件为cizi=y2。设各个考察期总收入、各种商品的单位价值、品种不变。进而得到如下两组方程：

借助于拉格朗日乘数法得到最优消费条件：

其中λt为第t期每单位收入给工人带来的边际效用，βt为第t期每单位收入给资本家带来的边际效用。由于工人收入低于资本家收入，所以λt＞βt，这意味着私有制下无法实现消费者帕累托最优。第t+1期情况。设资本家从自己的收入中拿出一部分Δy＞0分给工人。这时有如下方程：

于是得第t+1期工人和资本家作为消费者的最优消费条件：

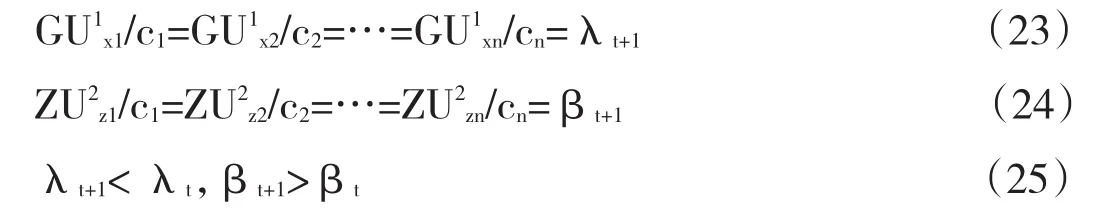
也就是说，随着工人价值收入的增加，其单位价值的边际效用随之递减，而相反，资本家随着价值收入的减少，其单位价值的边际效用随之递增。第t+n期。到t+n期总价值仍然不变，但是该资本家的价值收入的一部分转移给该工人，则可类推出如下结果：

则存在λ*、β*，使得λ*=β*。这时有

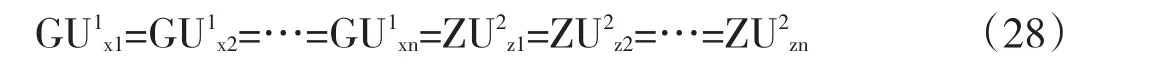
由（28）式得（∂GU1/∂xi）/（∂GU1/∂xj）=（∂ZU2/∂zi）/（∂ZU2/∂zj）。这就是消费性福利最优状态。注意到这一极限状态恰恰等价于公有制状态，因此公有制下消费者实现福利最优。证毕。

基于本文的分析，如果采用原则I，则可以保证公有制企业具有高效率。这一要素投入原则的深层含义是，公有制企业决策者的选拔对于公有制企业效率的提高具有决定意义。如何改变任人唯亲的低效率要素投入原则，选拔出德才兼备的企业家是公有制企业走出困境的关键。

[1]朱殊洋.马克思的生产函数[J].广东行政学院学报，2014，（6）.

□责任编辑：周权雄

F123.16

A

1003—8744（2016）06—0107—05

*本文系教育部人文社会科学研究项目《内需型经济增长方式下的就业均衡问题研究——以马克思再生产理论为框架》（编号：13YJA790129）、广东省哲学社会科学“十二五”规划项目《马克思经济增长理论研究》（编号：GD14CLJ01）的成果。

2016—10—7

徐跃华（1964—），女，广州大学马克思主义学院副教授，主要研究方向为政治经济学；朱殊洋（1959—），男，中共广州市委党校经济学教研部教授，主要研究方向为政治经济学。