组合预测模型在畜产品价格预测中的应用研究

潘文婧，赵安平，王大山，王晓东，肖金科

(北京市农业局信息中心，北京 100029)



组合预测模型在畜产品价格预测中的应用研究

潘文婧，赵安平，王大山，王晓东，肖金科

(北京市农业局信息中心，北京 100029)

频繁波动的畜产品价格已经成为影响我国居民消费价格指数的重要因素之一，如何准确预测价格走势以及时调整生产受到广泛关注。选取Holt-Winter季节乘积模型和ARIMA模型对2002—2015年北京市生猪、肉鸡、鸡蛋3种畜产品的市场周价进行实证研究，建立组合预测模型对价格进行拟合预测。模型评价结果显示，组合模型的预测精度最高，ARIMA模型次之，Holt-Winter季节乘积模型最差。利用组合预测模型对2015年7月之后5周的价格进行预测，结果显示组合预测模型在畜产品短期预测当中具有较好的准确性和可行性。

价格预测；组合预测模型；畜产品；时间序列

近年来，关于猪肉、鸡蛋等农产品价格大幅波动的报道频繁出现于各类媒体新闻上，对农业生产经营和居民消费都带来了非常大的困扰。在当前国情下，农产品价格大幅波动的根本原因是由于生产供应调整没有与需求相匹配，是信息不对称的结果。2013年，中央“一号文件”强调要“健全重要农产品市场监测预警机制”。2015年，国务院发布意见表明，农产品价格主要由市场决定。这意味着市场在价格调节方面的重要性越来越强，若能在复杂的市场背景下对畜产品市场价格走势做出较为准确的预判，将有利于生产经营者及时对市场做出反应并进行合理决策，有利于提高政府部门的管理效率和调控能力，为农业产业提供信息化支持，进而推动农业现代化发展。

在畜产品价格预测研究方面，有学者从长期价格变动趋势的角度进行定性分析[1，2]，更多的是用计量经济学等方法做量化分析。如，国外学者用Box-Jenkins法、线性回归法、指数平滑法、神经网络模型等方法对美国的牛肉价格[3]、生猪价格[4]、伊朗禽肉价格[5]进行了预测分析，预测结果均比较理想。我国学者的研究以生猪价格预测为主[6-9]，鲜有关于禽蛋产品价格预测的研究，且以单产品单模型预测为主，鲜有综合预测方法的应用。本文基于组合预测理论，结合时间序列分析方法，建立组合预测模型对北京市自2002年以来的生猪、肉鸡和鸡蛋价格进行拟合预测分析，旨在补充畜产品价格预测研究范畴，增强市场价格调控的可预见性。

1 畜产品价格组合预测模型的建立

1.1 数据来源

选取生猪、肉鸡、鸡蛋3种畜产品的批发市场价格作为研究对象。基础数据来源于2002年1月1日—2015年6月30日期间北京市农业局信息中心关于北京市8个批发市场(新发地、岳各庄、朝阳大洋路、通州八里桥、顺义石门、昌平水屯、城北回龙观和锦绣大地批发市场)的周价(加权平均价格)监测数据，单位为元/kg，共计706w，即每种畜产品的时间序列各包括706个样本，基本能够反映北京市批发市场畜产品价格的长期变动情况。此外，本文选择Eviews 6.0软件对数据做处理分析。

1.2 畜产品价格走势分析

对于农产品来说，受到生产的季节性、消费和供应的周期性以及成本上升等因素的影响，在价格走势上通常会呈现出季节性、周期性和趋势性等特征。本文所研究的生猪、肉鸡和鸡蛋均属于畜产品，一方面，在消费上具有典型的季节性；另一方面，在供应上具有典型的周期性，市场的供给量直接对畜产品市场价格产生影响，尤以猪周期最为显著。附图所示的北京市畜产品历史价格轨迹周期内生猪价格有3次显著的大幅波动，肉鸡和鸡蛋价格在历史运行轨迹中小周期性波形也都很明显。从价格趋势线可以看出，2002—2015年北京市畜产品的批发市场价格变化显著，在农产品供应总体均衡、局部偏紧的形势下，畜产品价格仍处于上升阶段，具有明显的趋势性。

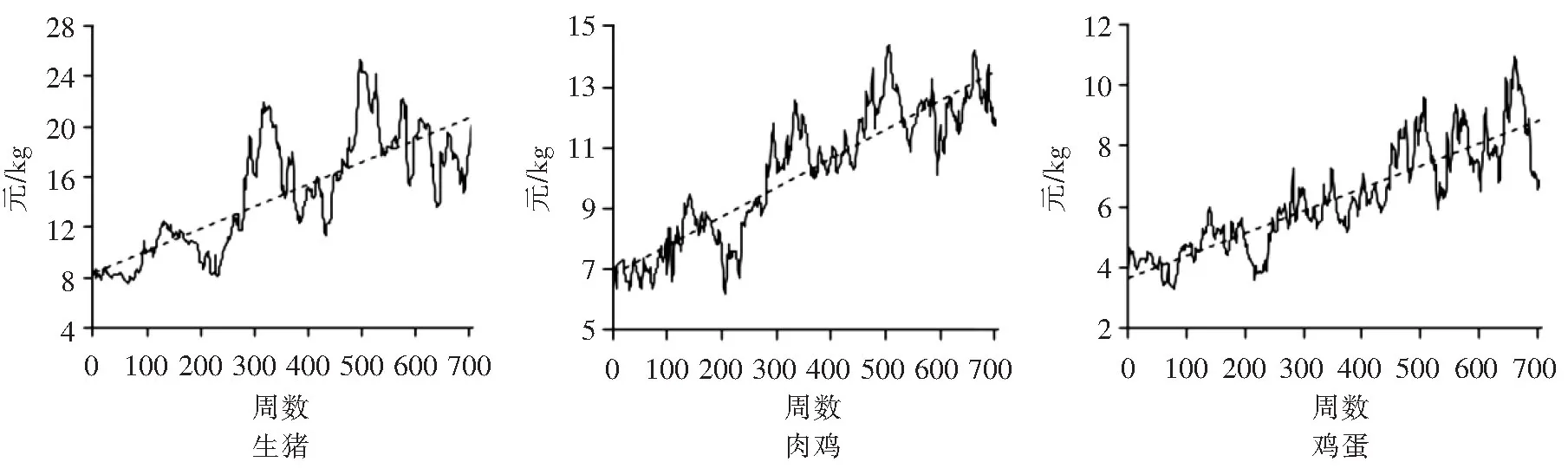
附图 2002—2015年北京市畜产品批发市场价格波动轨迹

1.3 预测模型理论构建

关于时间序列预测的方法有很多种，如：趋势外推法(截距变动模型、斜率变动模型等)、季节分解法(季节乘法模型和季节加法模型)、指数平滑法(一次指数平滑法、二次指数平滑法等)、Box-Jenkins法(AR模型、MA模型等)等。不同预测方法的前提条件也有所不同，基于前文对畜产品价格走势特征的分析，本文主要选择Holt-Winter季节乘积模型和ARIMA模型(差分自回归移动平均模型)2种模型进行拟合预测分析，并在此基础上构建组合预测模型进行探讨。

1.3.1 Holt-Winter季节乘积模型 Holt-Winter季节乘积模型属于较高级形式的指数平滑模型，是在二次指数平滑的基础上添加了用来描述周期性波动的量，因此，该模型适用于分析既有趋势又有季节波动的时间序列数据，主要反映近期数据的变化，适于短期预测。该模型有3个平滑参数α、β、γ(0≤α，β，γ≤1)，其表达式为式(1)：

(1)

1.3.2 ARIMA模型 ARIMA模型(差分自回归移动平均模型)适用于各领域的时间序列分析，是一种精度较高的时序短期预测方法[10]。ARIMA模型由自回归模型AR(p)和移动平均模型MA(q)组合而成，可表达为ARIMA(p，d，q)。其中，p表示自回归项、q表示移动平均项，d表示时间序列达到平稳时所做的差分次数，具体方程如式(2)：

Yt=φ1Yt-1+φ2Yt-2+…+φρYt-ρ-θ1εt-q+εt

(2)

式(2)中，φ1，φ2，…，φp为自回归系数；θ1，θ2，…，θq为移动平均系数；εt为WN(0，σ2)。

当序列平稳时，可由序列本身的滞后值和随机扰动项来解释。建模分为3个步骤：首先，平稳性检验；其次，模型识别；最后，参数估计检验。因此，ARIMA模型的求解关键在于对p、d、q三个统计参数的估计。参数d值通常用ARIMA模型平稳性检验来确定，参数p、q的值一般根据赤池信息准则(AIC)进行确定。AIC的取值范围为0～1，数值越小，意味着模型越好，越符合简约原则。模型建立后，需要对残差做单位根检验，若为白噪声结果，则可判定该模型拟合较好，能够用于实际预测分析。

1.3.3 组合预测模型 组合预测作为一种能够提高预测系统精度和稳定性的方法，一直受到国内外预测领域的广泛关注与应用。组合预测的类型基本可分为3种：串联型、并联型以及嵌套型[11]，这些组合方法都是通过对模型的取长补短来降低单模型的缺陷敏感度，以提升预测结果的准确性和稳定性。本文采用并联型组合预测模型，即给多个单模型的预测结果赋予不相等的权数，从而构建组合预测模型如式(3)：

(3)

式(3)中，m表示共有种单模型预测方法、fit为第i种预测方法在第t期的预测值、ki为第i种预测方法的权重。

权重ki的赋值方法包括：简单单纯型法、线性规划方法、广义递归方差倒数法、二次规划法、模糊综合数学法、层次分析法等。本文以误差平方和越小则权重越大为原则，采取方差倒数法计算权重。方法如式(4)：

(4)

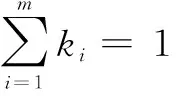
综上，本文建立组合预测模型如式(5)：

(5)

式(5)中，j表示第j种畜产品、f1tj表示第j种畜产品的Holt-Winter季节乘积模型预测值、f2tj表示第j种畜产品的ARIMA模型预测值。

2 畜产品价格组合预测模型的应用

2.1 模型结果评价

2.1.1 组合预测模型实证构建 运用Eviews 6.0软件的系统缺省模式对3组样本数据进行拟合，分别对时间序列的长期趋势、趋势的增量以及季节波动做出估计，得到北京市批发市场生猪价格序列的预测方程参数估计结果为：α=1、β=0.41、γ=0；肉鸡价格序列的预测方程参数估计结果为：α=1、β=0、γ=0；鸡蛋价格序列的预测方程参数估计结果为：α=1、β=0、γ=0(表1)。

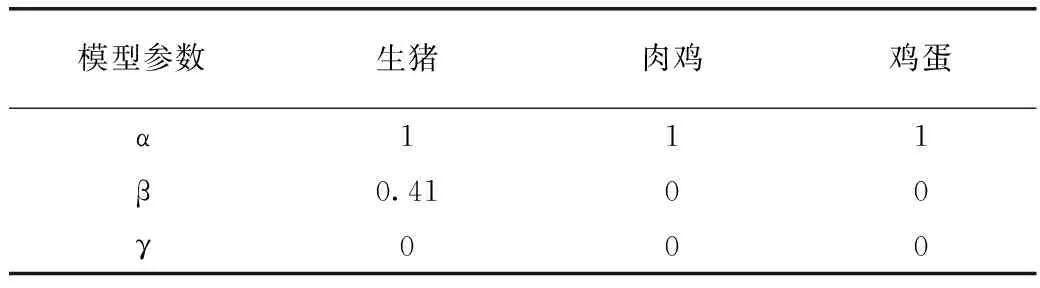
表1 Holt-Winter季节乘积模型参数结果

检验数据序列平稳性是建立ARMA模型的前提，经ADF单位根检验，北京市生猪批发市场价格、肉鸡批发市场价格、鸡蛋批发市场价格的时间序列均为一阶单整序列，即参数d1=d2=d3=1。通过观察3类畜产品一阶差分序列的自相关函数图和偏自相关函数图的截尾和拖尾情况，综合AIC准则、拟合优度及相关系数的显著性，并多次试验比较后，最终筛选确定了生猪、肉鸡和鸡蛋3种畜产品ARIMA模型的参数(表2)。

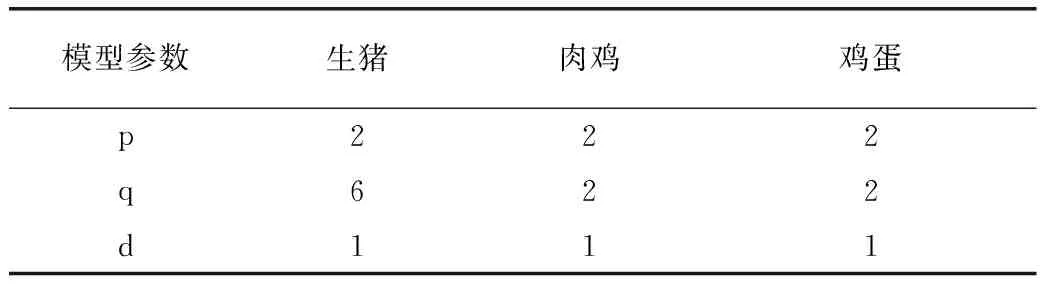
表2 ARIMA模型参数结果

将上述Holt-Winter季节乘积模型和ARIMA模型组合，并用方差倒数法进行权重计算分配后的模型最终结果如式(6)：

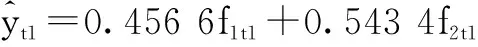
(6)

2.1.2 模型精度比较分析 预测精度通常被用来评价一个模型预测结果的好坏程度，常用的评价指标有：平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、残差平方和(SSE)、均方根误差(RMSE)、希尔不等系数(Theil)等。一般来说，这些表示预测误差的指标都是择小为优。本文选取平均绝对百分比误差(MAPE)和均方根误差(RMSE)2个指标作为评价模型结果的标准。其中，平均绝对百分比误差(MAPE)用于衡量模型的好坏，MAPE值越小说明预测值与实际值的差别越小，一般来说，MAPE值在0～5之间表示模型预测效果非常好，在6～10之间表示模型预测效果好[10]。计算方式如式(7)：

(7)

均方根误差(RMSE)通常用于测量预测值偏离真实值的程度，即样本的离散程度，取值范围在0～1之间。在实际预测中，预测次数总是有限的，真实值只能用最佳值来代替，所以均方根误差对误差值的高敏感度使得它能够很好的反映预测的精确度，可以作为评价模型精度的标准。计算方式如式(8)：

(8)

从表2的模型评价指标对比结果来看，生猪、肉鸡和鸡蛋3种畜产品所有模型的平均绝对百分比误差(MAPE)值都在1～3之间，表明这些模型的预测效果都非常好。而对比各产品各模型的均方根误差(RMSE)值可知，组合预测模型最小，ARIMA模型次之，Holt-Winter季节乘积模型最大。因此，可以认为组合预测模型的精度比任一单模型精度都高，且在单模型中Holt-Winter季节乘积模型精度高于ARIMA模型的精度。此外，由于本文选取的2种单模型本身预测结果精度都比较高，所以组合预测模型改善的幅度不太明显。在实际应用中，组合预测模型应比单模型具有更好的实用性。

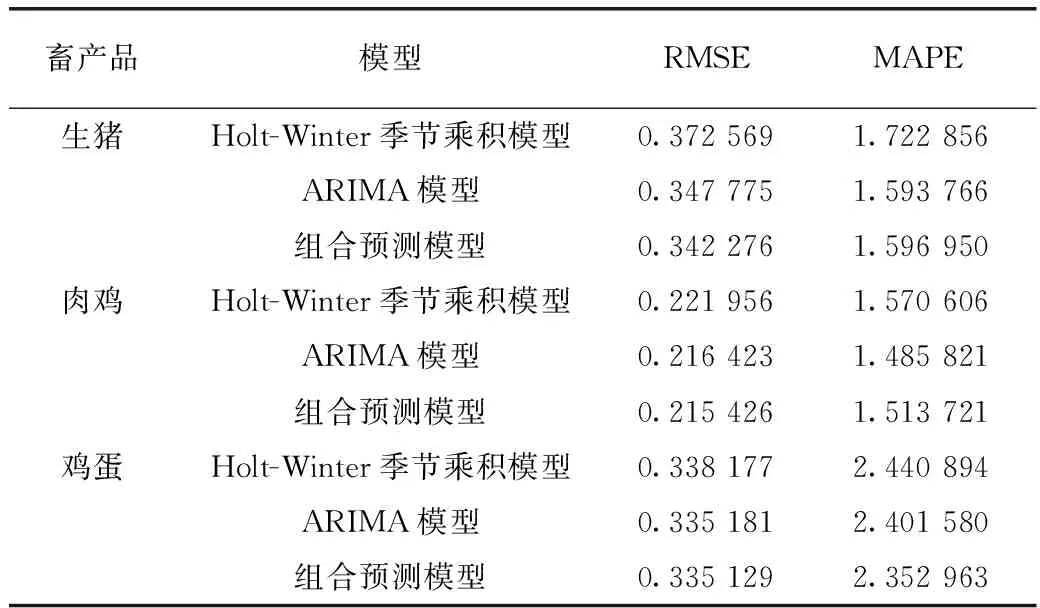
表3 预测模型结果汇总

2.2 组合预测模型的实证应用

基于模型评价结果，组合预测模型在生猪、肉鸡和鸡蛋3种畜产品价格中的预测效果最好。以2002年1月1日—2015年6月30日数据为基础，采用表1和表2中确定的模型参数，依据1～6式中各模型的权重，对2015年7月之后5周的北京市生猪、肉鸡和鸡蛋批发市场价格进行预测(表4)。

表4 北京市畜产品批发市场价格组合预测结果 单位：元/kg

北京市生猪和肉鸡价格变动情况与实际批发市场的行情基本吻合，且预测相对误差都很小。尤其对于2015年的生猪价格来说，疯狂的猪周期使得市场价格估计变的颇有难度，但预测结果误差都在5%以内，且最低相对误差仅为0.84%，再次说明了组合预测模型的精度较高。肉鸡价格的相对误差变化幅度很小，基本都在3%以内，误差波动较为稳定。相比之下，鸡蛋价格的预测值和市场行情略有不同，预测期内第5周的预测相对误差值较大，超过了10%，虽然相对误差在20%以下的模型结果都在可接受范围内，但从数据上看，一方面表明，在7、8月份交替时期，鸡蛋可能由于高温难存等因素造成了价格的异动性增长，另一方面也在某种程度上说明了预测的概率性和不确定性。

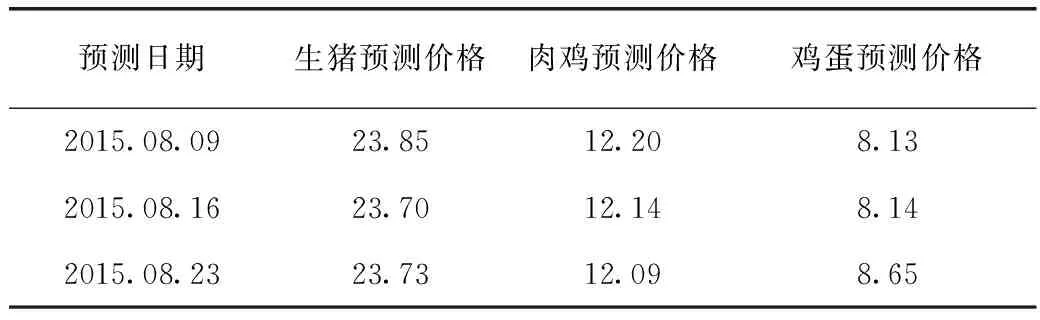
表5 北京市畜产品批发市场价格组合预测结果 单位：元/kg

在实证探讨了组合预测模型在北京市畜产品价格预测当中的表现后，表5给出了未来3期生猪、肉鸡和鸡蛋价格的预测价格。结果显示，未来生猪价格和肉鸡价格都将波动下降，而鸡蛋价格呈现逐周上涨的趋势。

3 结论与讨论

3.1 结论

(1)组合模型比单模型更适合于对畜产品价格做短期预测。本研究基于2002—2015年北京市畜产品批发市场周价格的大样本时间序列数据库建立了3组预测模型，根据历史数据拟合情况来看，通过权重配比将Holt-Winter季节乘积模型和ARIMA模型进行组合后的模型在价格预测方面比单项模型的预测结果要好，要更适合于对畜产品价格做短期预测。通过对北京市畜产品未来五期周价的预测，也基本印证了组合预测模型在实际市场应用中的可行性。(2)组合预测模型在生猪和肉鸡批发市场价格上的应用更为精确有效。根据组合预测实证分析结果，从总体上看，组合预测模型对生猪和肉鸡的的预测准确性基本在95%以上，且模型对北京市肉鸡批发市场价格预测的相对误差要低于生猪价格和鸡蛋价格的相对误差，鸡蛋市场价格的预测偏差相对不稳定，出现了一个较大的异常值。

3.2 讨论

一般来说，存在季节性的序列在建模前需要先通过一定的技术来消除季节性，但本文选取的两个单模型都可以在建模过程中直接处理序列的季节性问题，所以不做季节调整。这两种方法虽然在理论基础和数学方法上都不一样，但是存在同样的一个问题，即只考虑数据本身的信息，建模是为了预测而预测，虽用于经济数据分析，却缺乏经济理论基础。因此，如果能了解更多与畜产品价格波动相关的影响因素，并将其融入组合预测模型当中，对其进行深度挖掘，将在更大程度上推动组合预测结果的精度和价格预测的合理性。对于预测的精确度，它兼具近似性和局限性，但预测只是对未来的一种推测性的描述，并不等于将来的真实情况，我们在研究中应注意模型化问题，持辩证的态度去看待。◇

[1]张娜，周荣柱.生猪价格变化走势及后期预测[J].中国饲料，2014，6：40-41.

[2]李文煌.我国猪肉价格走势与生猪饲养业格局变化的相关分析[J].价格理论与实践，2013，7：60-61.

[3]Bourke，I.J.Comparing the Box-Jenkins and Econometric Techniques for Forecasting Beef Prices[J].Review of Marketing and Agricultural Economics，1979，47(2)：95-106.

[4]Schmitz，et al.Watts.Forecasting Wheat Yields：An Application of Parametric Time Series Modeling[J].American Journal of Agricultural Economics，1970，52(2)：247-254.

[5]Karbasi，A，et al.Comparison of NNARX，ANN and ARIMA Techniques to Poultry Retail Price Forecasting[J].International Association of Agricultural Economists，2009 Conference，August 16-22，2009，Beijing，China.

[6]丁琳琳，孟军.两种模型对中国生猪价格预测效果的比较[J].统计与决策，2012，4：74-76.

[7]郝妙，傅新红，陈蓉.灰色系统理论在生猪价格预测中的应用[J].中国农学通报，2014，30(14)：310-314.

[8]黄靖贵，等.基于面板数据模型的生猪价格风险评估及预测研究[J].中国畜牧杂志，2011，47(22)：59-62.

[9]马孝斌，王婷，董霞，等.向量自回归法在生猪价格预测中的应用[J].中国畜牧杂志，2007，43(23)：4-6.

[10]易丹辉.数据分析与Eviews应用(第二版)[M].北京：中国人民大学出版社，2009，8：122-151.

[11]平平.组合预测模型在吉林省生猪价格预测中的应用[D].吉林：吉林大学，2010.

(责任编辑 李婷婷)

Application of Combination Forecasting Model on Price Forecast of Animal By-products

PAN Wen-jing，ZHAO An-ping，WANG Da-shan，WANG Xiao-dong，XIAO Jin-ke

(Information Center of Beijing Municipal Bureau of Agriculture，Beijing 100029，China)

Frequent fluctuation of animal by-products price has become one of the important factors affecting China’s consumer price index，and how to accurately predict price movements and adjust production has been widely concerned.Empirical research on Beijing’s animal by-products’ including pig，poultry，and eggs weekly market price from 2002 to 2015 was conducted by adopting Holt- Winter Multiplicative Model and ARIMA Model.Based on these two single prediction models，the Combination Forecasting Model was set up to fit and predict the price.The results of the model evaluation indicated that the level of each model’s prediction accuracy ranked in a descending order from the Combination Forecasting Model to ARIMA model，then to Holt- Winter Multiplicative Model.The Combination Forecasting Model showed higher accuracy and feasibility in the short-term forecasting of the price of animal by-products，which was used to predict the market price of animal by-products in the subsequent five weeks after July 2015.

price forecast；Combined Forecasting Model；animal by-product；time series

北京市科技计划课题“北京畜产品市场价格风险预警与决策支持”(项目编号：Z141100006014040)。

潘文婧(1990— )，女，硕士，助理研究员，研究方向：农产品市场监测预警。

王大山(1972— )，男，学士，高级农艺师，研究方向：农产品市场体系建设。