打开一句话的世界——苏教版五上《钉子板上的多边形》教学实践与思考

彭文珍

打开一句话的世界——苏教版五上《钉子板上的多边形》教学实践与思考

彭文珍

钉子板上的多边形；皮克定理；教学实践；教学思考

20年前，在辅导学生趣味数学时，我就知道了皮克定理，当时学生不善提问，我也教得简单，只是告诉他们这个定理，然后让他们用它来解决各种变化的图形的面积计算问题。20年来，每次教到多边形的面积计算，遇到一两道稍难的问题，我都会忍不住告诉学生皮克定理，并立刻再出几道难题让他们用皮克定理来解决，每一次总能如我所愿地收获学生惊奇、狂喜的目光。

如今，皮克定理已经走进了学生的数学课本。一次要上一节市级公开课，我想也不想就把课题定为它，我要将一句话变为一节课来好好地演绎皮克定理。

环节一：分析

师：这是老师昨晚留下的思考题，图1中这个多边形的面积是多少？

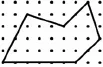
（图1）

生：24平方厘米。

学生简要介绍分、补、移等方法。

师：用分和补做这道题，过程往往特别长，全班最多的好像是28步。如果图形再多拐几个弯，估计算式会更长。解决这样的问题还有没有其他的方法？

师：你们看，老师给图形加了格点，你们觉得图形的面积可能和什么有关？

生：和点，和图形里面的点以及边上的点的个数有关。

师：有可能有关系，也有可能没关系，所以咱们这节课就来研究它。这一个个点像钉子，我们就叫它“钉子板上的多边形”。

环节二：探路

师：图形里面的点简称内点，用字母a表示，边上的点简称边点，用字母b表示，面积用字母S表示。在钉子板上可围的图形太多了，为了便于发现规律，你们觉得应该先研究什么样的图形？

生：长方形、正方形、平行四边形……

师：为什么先选择这些图形？

生：这些图形我们都学过，可以直接用公式来计算它们的面积。

师：还有补充吗？

生：先研究点少的图形，再研究点多的。

【探究一】

（图2）

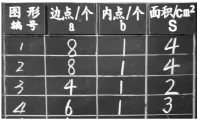
教师出示图2，引导学生研究钉子板上的四个多边形，并把研究结果填入表格中。

师：你们发现其中的规律了吗？

生1：a÷2=S，边点÷2=面积。

生2：a×b÷2=S，内点×边点÷2=面积。

生3：我觉得第二个比第一个好，它把内点也用起来了。

生4：我发现多边形的面积可能真的和点有关系，1号和2号图形形状不同，但它们边点和内点的个数相同，面积也相同。

师：为了验证你们说的规律，下面我们来研究内点数是2的图形。

【探究二】

（图3）

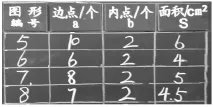
教师出示图3，引导学生研究并填写表格。

生1：我发现刚才的规律不对，应该是（a+b）÷2= S，（边点+内点）÷2=面积。

生2：我们应该继续研究内点数是3的图形，看是否有其他的规律。

【探究三】

（图4）

教师出示图4，引导学生继续研究并填写表格。

生1：我发现刚才的规律又不成立了，应该是（a+b+1）÷2=S，（边点+内点+1）÷2=面积。

生2：我发现三次探究的规律了，图形的内点数为1时是a÷2=S，内点数为2时是（a+b）÷2=S，内点数为3时是（a+b+1）÷2=S，内点数为4时是（a+b+2） ÷2=S。我画了有4个内点的正方形和5个内点的梯形，也符合这个规律。

生3：我觉得他说得很对，不过我换一个角度发现了一个新的规律，我从第一个规律a÷2开始，图形有1个内点时是a÷2=S，2个内点时是a÷2+1=S，3个内点时是a÷2+2=S，4个内点时是a÷2+3=S。

环节三：挑战

师：如果上述规律成立，怎么用一句话来概括这个规律？

生：a÷2+（b-1）=S，也就是a÷2+b-1=S，边点÷2+内点-1=面积。

师：现在我们好像找到了一个从头到尾都成立而且很简洁的规律，接下来你想干什么？

生：自己画图验证。

环节四：反思

师：回顾这节课，你还有什么想问、想说的？

生1：太奇妙了，我想知道为什么。

生2：其实刚才我也发现了，内点数是3时是（a+b+1）÷2=S，用字母公式表示是（a+b+b-2）÷2=S，即（a+2b-2）÷2=S，也就是a÷2+b-1=S。

师：听明白他的意思了吗？看来看似不一样的算式，变一变可能一样。

生3：我想知道这个规律是谁第一个发现的，它有什么用。

课件介绍数学家乔治·皮克和皮克定理。

对于皮克定理，我研究了20年，研究的结果是：那些解释都太深奥，我无法让学生也明白。因此，每一年我都是以一句话的形式将它直接告诉学生。选择这个课题来上公开课，同事们都说：“这有什么好上的？就一个公式，一点就破。”可是，课堂上学生却探究出了一个又一个成立的公式，连听课教师都忍不住说：“还真对呢！”每一个公式的得出都是一份欣喜，每一个小小的发现却又只是拔根“小刺”，直至“大钉子”被寻出。这节课没做什么巩固练习，学生却有条理地进行了大量的基础性研究。看学生到课末都兴趣盎然，我不禁自问：在我们自认为终结的世界里，还有多少没被打开的空间？

学生在自己的世界里寻找到了自己的解释，并创造出了自己的答案。我不知道还有多少未知能变成已知，为人师的我们都该重新审视我们的知识和经验世界！

G623.5

A

1005-6009（2016）52-0056-02

彭文珍，江苏省海安县明道小学（江苏海安，226600），一级教师，南通市骨干教师。