社团结构对网络稳定性的影响分析

刘婉璐，叶永升

（淮北师范大学 数学科学学院，安徽 淮北 235000）

社团结构对网络稳定性的影响分析

刘婉璐，叶永升

（淮北师范大学 数学科学学院，安徽 淮北 235000）

利用CSEN模型建立具有社团结构的复杂网络，并用CNM算法对所建立的网络进行社团结构分析，基于CML的相继故障模型对所建立的网络进行随机及蓄意攻击，探讨社团结构对网络稳定性的影响.结果表明网络社团结构强度越大，网络的稳定性越强；网络稳定性存在一个界值，一旦网络受到攻击大于某阈值，故障会迅速扩大到整个网络，从而造成整个网络崩溃.同时，给出不同社团结构对应的网络所能承受的随机及蓄意攻击的阈值，为监控网络安全调整网络稳定提供参考.

CSEN模型；社团结构；CNM算法；网络稳定性

0 引言

现实生活中很多系统都可看作一个网络，随着信息全球化的飞速发展，网络的规模不断扩大，节点间的联系也更加复杂，大规模的复杂网络成为学术界的研究热点［1］.随着对复杂网络的深入研究，人们发现很多网络都有一个共同性质——社团结构［2］，所谓社团即是将网络中的节点划分成不同组，组内节点联系比较稠密，组间节点联系比较稀疏.

近年来，很多学者更加关注对大规模复杂网络的安全稳定性研究.文献［3］采用变量梯度分析法研究网络的稳定性，文献［4］对非线性动力系统构成的复杂网络进行研究，分析该网络的同步性及随机稳定性.考虑到社团结构是复杂网络的重要结构属性［5］，本文将结合网络的社团结构性对网络稳定性进行分析，探讨社团模块度Q与网络稳定性的关系，揭示破坏网络稳定性和引起网络崩溃的内在机制.

1 建立网络

为了探讨社团结构与网络稳定性之间的关系，首先需要建立具有社团结构的网络模型.此处，运用具有社团结构的网络演化模型——CSEN模型［6］生成网络，CSEN模型即Community Structured Evolving Network Model.

具体算法过程如下：

第1步：初始化.设初始网络中有c0(c0＞1)个社团，各个社团的内部由n0个两两相连的节点构成，且这c0个社团由c0(c0-1)/2条边连接.

第2步：社团增长.以概率p向网络中添加一个新社团.该社团仍是由n0个两两相连的节点所构成.从新社团中任选一个节点，经过m条边与其他社团内的节点相连接.

第3步：节点增长.以概率1-p向该网络中添加一个新节点.该节点按照社团规模优先机制［7］选择一个社团并加入，对该节点引入m条边，这m条边以概率q与该节点所在社团内的其他节点相连，而以概率1-q与其他社团内的节点相连.

第4步：返回第2步，直到网络达到所需规模为止.

通过多次随机独立实验的统计平均，得到该模型所生成网络的集聚谱分布（如图1所示）.

图1 集聚谱分布

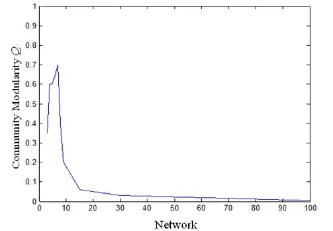
图2各个网络对应的社团模块度Q

图1 中k表示节点，C(k)表示节点的集聚谱，此为100组数据得到的平均结果.结果表明，生成的网络聚类系数较大，平均最短路径长度较短，且通过简单的参数调整即可控制网络.

2 分析生成网络的社团结构

以下采用Newman贪婪（CNM）算法［8］，对Q函数及辅助向量进行改进，并采取Clauset、Newman和Moore设计的数据结构来存储和更新Q函数，及对网络进行社团化处理.

具体过程如下：

第1步：初始化.将网络中的每个节点都看作一个社团，初始的模块度值Q=0.若节点i、j有边相连，则边权eij=1；若节点i、j无边相连，则边权，以a作为辅助向量，其元素.对ΔQ矩阵初始化，该矩阵元素满足ΔQ=2(e-aa)，显然ΔQ矩阵是稀疏矩阵.ijijij

第2步：从初始化的ΔQ矩阵中选取每行的最大元素，构成最大堆H.

第3步：从最大堆H中找到最大的ΔQij，将对应的社团i、j进行合并（不妨设i＜j），将合并之后的社团标记为j，并对矩阵ΔQ、最大堆H及辅助向量a进行更新.

第4步：重复第2步，直到将所有的ΔQij由正值变为负值.

最终，得到100组节点不同的网络的模块度值Q（如图2所示）.

3 社团结构对受攻击下的网络稳定性影响

为研究网络在受攻击下的稳定性，在此采用随机攻击和蓄意攻击［9］2种攻击方式.随机攻击即随机地移除某些节点及与其相连的所有边；蓄意攻击即有意地移除某些介数较大的节点及与其相连的边.若抗攻击性较强则称网络有较强的鲁棒性，即认为网络的稳定性较强，否则认为网络的稳定性较弱.图3给出了网络稳定性阈值Rc随社团模块度Q的变化关系.

图3 网络稳定性阈值Rc随社团模块度Q的变化关系

基于耦合映像格子（CML）的相继故障模型［10］通过网络受到扰动R所能达到的阈值Rc（当R≥Rc时网络中所有的节点都在下一时刻发生故障）的大小来衡量关联网络的稳定性.在模拟过程中，对应相同的社团结构选择相同的节点进行随机攻击（蓄意攻击采取同样的方法）.数值实验采取的参数m=5，ε=0.6，N在[1 325,1 425]之间，其中m指攻击某个节点的时刻，ε指耦合强度，N指网络规模，100次实验之后得到网络稳定性随社团模块度Q的变化关系（如图3所示）.

从图3可以看出，无论是随机攻击还是蓄意攻击，阈值Rc都随着社团模块度Q的增加而增加.这说明网络社团模块度Q越大其鲁棒性越强，Q越小网络越脆弱.当Q值靠近0时，无论是随机攻击还是蓄意攻击，较小的扰动都可能造成网络的崩溃.

4 总结与展望

本文分析了复杂网络稳定性与社团结构之间的相互关系，经100组实验得到的平均数据可知，社团模块度Q越大网络鲁棒性越强，即网络越稳定，Q越小网络越脆弱.给出了各个Q值对应的攻击阈值Rc，即随机或蓄意攻击网络某些节点，当R≥Rc时，网络中的所有节点都在下一时刻发生故障.这对现实网络的监控和调整有一定的指导意义，如在股票市场中可根据社团模块度Q及市场受攻击的大小R对网络进行有效地调整和监控.另外，在攻击R临近阈值Rc时，重点调整哪些节点才能避免下一时刻所有节点都发生故障，是进一步需要探讨的问题.

［1］BARABASI A L.Linked：The new science of networks［M］.Massaehusetts：Persus Publishing，2002.

［2］汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.北京：清华大学出版社，2006.

［3］毛凯.复杂网络结构的稳定性与鲁棒性研究［J］.计算机科学，2015，42（4）：85-88.

［4］严洲.复杂网络随机稳定性和同步性研究［D］.杭州：浙江大学，2012.

［5］FORTUNATO S，CASTELLANO C.Community structure in graphs［J］.Encyclopedia of Complexity&Systems Science，2007（12）：490-512.

［7］LI Chunguang，CHEN Guanrong.Modeling of weighted evolving networks with community structures［J］.Physica A，2006，370（2）：869-876.

［8］CLAUSET A，NEWMAN M E J，MOORE C.Finding community structure in very large networks［J］.Physical Review E，2004，70（6）：066111.

［9］CRUCITTI P，LATORA V.Error and attack tolerance of complex networks［J］.Physica A，2004，340（1/2/3）：388-394.

［10］WANG Xiaofan，XU Jian.Cascading failures in coupled map lattices［J］.Physical Review E，2004，70（5）：056113.

Effects Analysis of Community Structure on Stability of Complex Networks

LIU Wanlu,YE Yongsheng
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

Complex networks with community structure are constructed by using the CSEN model，and commu⁃nity structures are detected by the CNM algorithm in the constructed networks.Random and deliberate attack⁃ing on the networks based on the CML cascading failures model is used to find the relationship between com⁃munity structures and stability of networks.The results show that the greater modularity means the stronger stability and robustness of networks，and there is a critical value.Once the networks are attacked greater than the value，failures will expand to the entire networks fast，and the entire networks will collapse.The critical values that adjust different community structures under random or deliberate attacking are given.All results provide a reference for monitoring network security and regulating the network stability.

CSEN model；community structure；CNM algorithm；stability of complex networks

O 29

A

2095-0691（2016）04-0030-03

2016-07-06

国家自然科学基金项目（61300048）；安徽省自然科学研究项目（1408085MA08）；安徽省高校自然科学研究项目（KJ2016A633）

刘婉璐（1988- ），女，安徽淮北人，硕士，助教，研究方向：复杂网络.