一类具时滞和比率依赖的捕食-食饵模型2个周期解存在性

吴书韬，梁 峰

（安徽师范大学 数学计算机科学学院，安徽 芜湖 241003）

一类具时滞和比率依赖的捕食-食饵模型2个周期解存在性

吴书韬，梁 峰

（安徽师范大学 数学计算机科学学院，安徽 芜湖 241003）

研究一类带有HollingIII型反应函数的捕食-食饵模型

周期解；Mawhin重合度拓展定理；时滞；捕食-食饵模型；比率依赖

0 引言

由于捕食和食饵的普遍存在性和重要性，它们之间的动态平衡问题一直是生态学和数学生态学中一个重要研究课题.前些年，传统捕食-食饵模型被广泛研究［1-3］.现阶段，由文献［4-6］知，存在更直接的生物学和生理学证据，其表明在许多情形下，尤其是捕食者之间不得不存在竞争或分享食物时，应该在基于比率的情形下，建立一个更具一般性的捕食-食饵模型［7-8］.许多研究者已经研究带有或不带时滞的基于比率依赖的捕食-食饵模型，并且研究了它们的动力学性质［9-19］.

鉴于实际问题的周期性，文献［18］研究了带有时滞和基于比率的捕食-食饵模型的周期解存在问题：

在（1）式中加入HollingIII反应函数，文献［19］研究了具有时滞和HollingIII型基于比率的捕食-食饵模型的周期解问题：

然而，对此类系统的带有2个周期解存在性的研究结果相对较少.

受以上研究结果启发，在本文中，我们研究具有时滞和HollingIII型基于比率的捕食-食饵模型的2个周期解存在性问题：

在这里，a,b,c1,c2，r1，r2，τ1，τ2是周期为T的连续非负周期函数，m＞0，K(s):R+→R+是可测函数，且满足.这里r1(t)代表食饵的内禀增长率，m代表半捕捉饱和常数，r2(t)代表捕食者死亡率，c1(t)和c2(t)代表转化率；函数代表在没有捕食者时食饵的比生长速率；x2(t)/(m2y2(t)+x2(t))代表捕食者反应函数（反映了捕食者的捕食能力）.运用Mawhin重合度拓展定理［20］，本文证明系统（3）存在2个正周期解.

1 周期解的存在性

令X，Y是Banach空间，L:Dom L⋂X→Y是线性映射，N:X→Y是一个连续映射.如果L为指标为零的Fredholm映射且存在连续投影P:X→X，及Q:Y→Y使得Im P=Ker L，Ker Q=Im L=Im(I-Q)，则L|DomL⋂KerP:(I-P)X→Im L是可逆的.设其逆映射为 Kp.如果 Ω是 X中的有界开集，有界且Kp(I-Q):是紧的,则称 N在是 L-紧的.由于 Im Q与 Ker L同构，故存在同构映射J:Im Q→Ker L.下面的Mawhin重合度拓展定理是证明本文结论的主要工具.

2 例子

例1 在系统（3）中，令

则可得

那么可验证（h1）和（h2）成立.因此，由定理1，可知系统（3）至少有2个不同的正周期解.

注2 由于只有相对较少的文献考虑具有时滞和HollingIII型基于比率的捕食-食饵模型的多个周期解问题，所以本文结果相对来说是较为新颖的.

［1］ZHANG Zhengqiu，HOU Zhenting，WANG Li.Multiplicity of positive periodic solutions to a generalized delayed predatorprey system with stocking［J］.Nonlinear Anal，2008，68：2608-2622.

［2］DING Xiaoquan，JIANG Jifa.Positive periodic solutions in delayed Gause-type predator-prey systems［J］.J Math Anal Ap⁃pl，2008，339：1220-1230.

［3］HU Xiaoling，LIU Guirong，YAN Jurang.Existence of multiple positive periodic solutions of delayed predator-prey models with functional responses［J］.Comput Math Appl，2006，52：1453-1462.

［4］KUANG Y，BERETTA E.Global qualitative analysis of a ratio-dependent predator-prey system［J］.J Math Biol，1998，36：389-406.

［5］JOST C，ARINO O，ARDITI R.About deterministic extinction in ratio-dependent predator-prey models［J］.Bull Math Bi⁃ol，1999，61：19-32.

［6］HSU S，HWANG T，KUANG Y.Global dynamics of a predator-prey model with Hassell-Varley type functional response［J］.J Math Biol，2008，10：1-15.

［7］HANSKI I.The functional response of predator：worries bout scale［J］.TREE，1991，6：141-142.

［8］ARDITI R，PERRIN N，SAIAH H.Functional response and heterogeneities：an experiment test with cladocerans［J］. OIKOS，1991，60：69-75.

［9］LIU Xiangsen，LI Gang，LUO Guilie.Positive periodic solution for a two-species ratio-dependent predator-prey system with time delay and impulse［J］.J Math Anal Appl，2007，325：715-723.

［10］SAHA T，BANDYOPADHYAY M.Dynamical analysis of a delayed ratio-dependent prey-predator model within fluctuat⁃ing environmen［tJ］.Appl Math Comput，2008，196：458-478.

［11］XIAO Dongmei，LI Wenxia，HAN Maoan.Dynamics in a ratio-dependent predator-prey model with predator harvesting［J］.J Math Anal Appl，2006，324：14-29.

［12］RYU K，AHN I.Positive solutions for ratio-dependent predator-prey interaction systems［J］.J Differential Eqns，2005，218：117-135.

［13］DAI Binxiang，ZHANG Na，ZOU Jiezhong.Permanence for the Michaelis-Menten type discrete three-species ratio-depen⁃dent food chain model with delay［J］.J Math Anal Appl，2006，324：728-738.

［14］AKHMET M，BEKLIOGLU M，ERGENC T，et al.An impulsive ratio-dependent predator-prey system with diffusion［J］. Nonlinear Anal RWA，2006，7：1255-1267.

［15］FAN Yonghong，LI Wantong.Global asymptotic stability of a ratio-dependent predator-prey system with diffusion［J］.J Comput Appl Math，2006，188：205-227.

［16］DEANGELIS D，HOLLAND J.Emergence of ratio-dependent and predator-dependent functional responses for pollination mutualism and seed parasitism［J］.Ecol Model，2006，191：551-556.

［17］WANG Mingxin.Stationary patterns for a prey-predator model with prey-dependent and ratio-dependent functional re⁃sponses and diffusion［J］.Phys D：Nonlinear Phenom，2004，196：172-192.

［18］FAN Meng，WANG Ke.Periodicity in a delayed ratio-dependent predator-prey system［J］.J Math Anal Appl，2001，262：179-190.

［19］WANG Linlin，LI Wantong.Periodic solutions and permanence for a delayed nonautonomous ratio-dependent predatorprey model with Holling type functional response［J］.J Comput Appl Math，2004，162：341-357.

［20］GAINES R，MAWHIN J.Coincidence degree and nonlinear differential equations，Lecture notes in math［M］.Berlin：Springer，1977.

Existence of Two Periodic Solutions for a Generalized Delayed Ratio-dependent Predator-prey Model with Holling Type III Functional Response

WU Shutao，LIANG Feng
（School of Mathematics and Computer，Anhui Normal University，241003，Wuhu，Anhui，China）

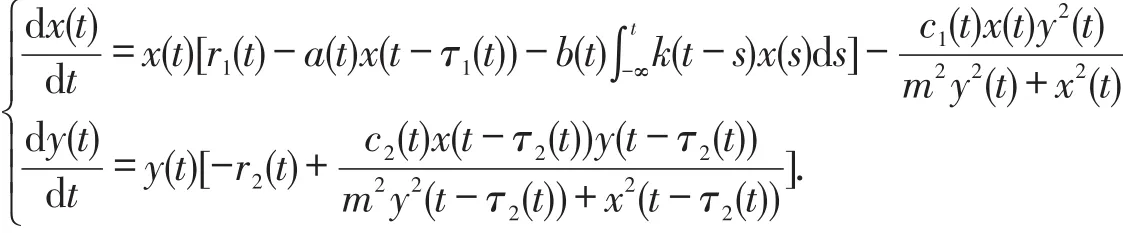
periodic solutions；Mawhin′s continuation theorem；delay；predator-prey model；ratio-dependent.

O 175

A

2095-0691（2016）04-0015-07

2016-04-11

安徽省自然科学基金项目（1308085MA08）

吴书韬（1991- ），男，安徽安庆人，硕士，研究方向：泛函微分方程.通信作者：梁峰（1974-），男，安徽太和人，博士，副教授，研究方向：微分方程理论及应用.

运用重合度拓展定理，证明其存在2个正周期解.并举一个实例验证结论的可行性.