成组不等径直槽丝锥的优化设计及有限元分析

王晓煜，张洋 ，李荣华 ，周颖

(大连交通大学 机械工程学院，辽宁 大连 116021)*



成组不等径直槽丝锥的优化设计及有限元分析

王晓煜，张洋 ，李荣华 ，周颖

(大连交通大学 机械工程学院，辽宁 大连 116021)*

对使用1 1/4-7UNC成组等径直槽丝锥加工高硬金属材料时会出现攻丝扭矩大，易扭断并且加工螺纹精度低等问题.为解决这一工艺难题，在对成组丝锥攻丝受力与扭矩分析的基础上，决定对其进行不等径设计.以减小攻丝扭矩和提高加工螺纹精度为目标，对其几何参数进行了优化设计.建立两组丝锥三维实体模型，然后进行有限元分析.将两组丝锥分析出来的结果进行对比，可以看出优化后成组不等径直槽丝锥结构合理.并且加工出来的螺纹表面质量，精度和使用寿命均有所提高.

高硬金属材料；成组不等径直槽丝锥；有限元分析

0 引言

在高硬金属材料的攻丝过程中，为减少丝锥刀齿负荷，往往采用成组丝锥攻丝，通过合理的分配切削负荷，完成攻丝加工过程[1].在使用大螺距成组等径直槽丝锥加工高硬金属材料时，由于材料硬度高，粗、中锥切削锥角小，切削部分长，切削厚度小，使切削变形增大，攻丝扭矩增大，丝锥易扭断导致所加工螺纹精度低甚至工件报废.所以在使用成组丝锥攻丝时，攻丝扭矩要小，并且每支丝锥的切削负荷要合理分配.攻丝过程中一定要注意攻丝扭矩的大小，攻丝扭矩过大会导致丝锥刀齿的断齿或扭断；并且在高扭矩的状态下，会使切削温度升高，而导致丝锥刀齿的磨损和降低丝锥的使用寿命[2].本文针对1 1/4-7UNC成组等径直槽丝锥攻丝高硬金属材料过程中出现攻丝扭矩大，加工螺纹精度低等问题，对其进行不等径设计，并对其几何参数进行优化设计.然后进行三维实体建模，通过有限元法来证明优化后丝锥的合理性.

1 成组等径丝锥和成组不等径丝锥

成组等径丝锥是指每支丝锥的大径、中径和小径的尺寸相同，区别仅在于切削锥角不一样[3].粗锥锥角最小，中锥次之，精锥最大.由于采用等径设计，每一支丝锥中径尺寸相同，粗锥和精锥之间无区别.因此，被加工螺纹的表面质量较差，其切削图形如图1所示.

图1 成组等径丝锥切削图

成组不等径丝锥是指每支丝锥的大径、中径和小径的尺寸各不相同.这种丝锥在切削时，齿顶、齿侧均具一定的吃刀量，并且每支丝锥对螺纹的齿廓都具有修正的作用，不会出现重复加工造成工件表面的刮伤，所以加工螺纹表面质量好.由于切削负荷分配合理，所以丝锥的使用寿命有所提高，其切削图形如图2所示.

图2 成组不等径丝锥切削图

2 成组丝锥攻丝受力和扭矩分析

成组丝锥每支丝锥的受力形式是一样的，将丝锥划分为无数个单元，以丝锥的第i个刀齿作为研究对象，按刀齿与工件间的相互作用关系.切削刃上的总切削力Fi，可以分解为主切削力分力Fc、径向力分力Fp和轴向力分力Ff.在刀齿两侧后刀面以及主后刀面上存在着刀面与工件之间的相互挤压产生的正压力Ni及摩擦力Ri[4]，如图3所示.

图3 丝锥的受力状态

丝锥攻丝扭矩一般的经验公式表示为[5]：

式中，M为攻丝扭矩，C为被加工的材料的系数，do为丝锥大径，P为螺距，Z为丝锥容屑槽的槽数，kr为丝锥锥角.

从攻丝扭矩公式中可以看出，在螺距和丝锥容屑槽的槽数确定后，攻丝扭矩与所加工材料、丝锥大径和锥角有关.由于1 1/4-7UNC成组等径直槽丝锥每支丝锥的大径相同，而粗、中锥锥角小，切削锥长，所以攻丝扭矩大，易扭断.而采用不等径设计每支丝锥的大径不同，所以可以考虑将其设计为成组不等径直槽丝锥.以减小攻丝扭矩为目标，将每支丝锥的几何参数进行优化设计，通过合理的分配切削负荷，从而延长丝锥的使用寿命，提高加工螺纹表面的粗糙度和精度.

3 成组不等径直槽丝锥的优化设计

3.1 优化设计方案

成组不等径直槽丝锥优化设计的方案是将粗、中丝锥采用等中径设计，而每支丝锥的大径依次增大.将精锥的中径和大径尺寸设计为所加工螺纹的要求.这样，由于粗、中丝锥的大径都有所减小，并且丝锥切削部分做短，切削锥角增大，切屑变厚，单位面积切削力减小.这样即可以减小攻丝扭矩，又可以避免切屑过薄，造成切削刃在硬化层上摩擦而加速丝锥磨损.在切削负荷分配合理的情况下，精锥保留有一定的吃刀量，可以保证加

工螺纹精度和表面粗糙度.

3.2 成组不等径直槽丝锥的设计

3.2.1 确定每支丝锥的负荷分配比例

在成组不等径丝锥中，粗锥要完成攻丝过程中大部分金属的切除，而精锥的切除量较小.所以，从丝锥的使用寿命和切削量上去考虑，以便确定每支丝锥切削负荷的分配.在成组丝锥中，当粗锥切削负荷小于40%时，粗锥切出的齿槽过浅而导致后续丝锥无法正常的导入加工，容易发生乱扣的现象.因此，粗锥的切削负荷都要按大于40%来设计.当精锥切削负荷小于8%时，精锥对粗、中锥所加工螺纹无修正作用，这将影响螺纹成品精度[6].通过上述分析，确定在丝锥的设计时采用粗锥切削面积占全部牙型面的60%，中锥占30%，精锥占10%.

3.2.2 计算每支丝锥的大径、中径

精锥螺纹大径、中径按GB968-2007《公制、美制和英制螺纹标准手册》确定，精锥大径为dI=31.85 mm，精锥中径为d2I=29.47 mm.

粗锥和中锥的大径按下式计算(dIII、dII分别为粗锥大径和中锥大径)：

dIII=dI-0.325P=30.67mm

dII=dI-0.108P=31.45mm

粗锥和中锥的中径计算(d2III、d2II分别为粗锥中径和中锥中径)：

d2III=d2II=d2I-0.271P=28.49 mm

3.2.3 确定每支丝锥切削部分长度

由于粗锥要完成攻丝过程中大部分金属的切除，为避免粗锥发生崩刃或者扭断，粗锥的切削部分长度要尽可能长一些.精锥的切削量较小，为防止因切屑过薄而造成切削刃的摩损致使丝锥的加速磨损，所以精锥的切削长度尽可能短.综合考虑后确定：粗锥切削长度取7P，中锥切削长度取4P，精锥切削长度取2P.

3.2.4 各支丝锥的锥角计算

切削部分长度L、螺纹计算高度为H与锥角φ的关系为：

经计算粗锥φ1=4.5°，中锥φ2=7.9°，精锥φ3=10.5°.

经过以上计算，得到优化后成组不等径直槽丝锥参数，如表1所示.

表1 优化后成组不等径直槽丝锥参数

原成组等径直槽丝锥参数如表2所示.

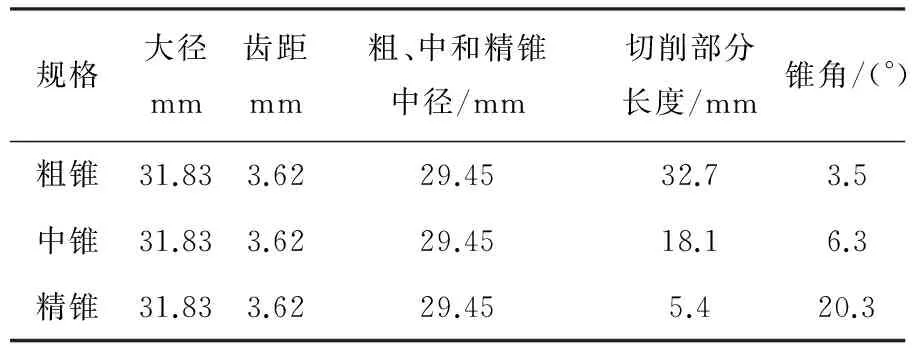
表2 原成组等径直槽丝锥参数

3.3 优化后成组不等径直槽丝锥与原成组等径直槽丝锥扭矩大小对比

通过前面两组丝锥的参数和扭矩计算公式可以算出每支丝锥扭矩的大小(扭矩单位为N·m)，经过计算，优化后成组不等径直槽丝锥粗(212.2<246.4)、中丝锥的扭矩比原成组等径直槽丝锥小(191.1<219.5).只有精锥扭矩稍大(182.8>173.7)，但是扭矩较小，不影响加工.所以，以上的优化设计是合理的.

4 优化后成组不等径直槽丝锥的有限元分析

由于采用传统设计方法无法对两组丝锥的强度及应力应变进行精确的分析.因此，本文采用有限元法对其进行分析.由于在攻丝的过程中只有切削部分与校准部分参与切削，所以在进行丝锥的有限元分析时可以忽略丝锥柄部的影响[7].边界条件包括模型的约束和载荷.由于在攻丝过程中所有自由度均被约束，固在模型方柄四周全部加上固定约束[8].丝锥的工作部分由切削部分和校准部分两部分组成，切削部分磨出锥角以使切削负荷分配到几个切削齿上.而校准部分有完整的齿形主要起引导丝锥轴向运动的作用.所以在丝锥切削部分的每个切削齿上施加所受的主切削力、轴向力和径向力载荷，模拟丝锥切削时每齿的受力情况.由于每支丝锥所施加力的情况相同，所以只展示优化后成组不等径直槽丝锥精锥荷施加情况,如图4所示.

图4 优化后成组不等径直槽丝锥精锥载荷施加情况

对两组丝锥进行有限元分析，可以得到两组丝锥最大应力(应力单位为MPa)和最大应变值(应变单位为mm)的大小.经过分析，优化后成组不等径直槽丝锥粗(10.16<12.43)、中(15.39<20.19)、精(19.67<28.67)三只丝锥的最大应力均比原成组等径直槽丝锥要小. 优化后成组不等径直槽丝锥粗(0.011<0.015)、中(0.027<0.06)、精(0.037<0.043)三只丝锥的最大应变也均比原成组等径直槽丝锥小.

以上分析是将切削力合理的分配到齿面上所得到的，由于机械应力是造成丝锥损坏的主要原因，所以通过有限元方法可以验证丝锥能否达到攻丝的要求和分析两组丝锥实际的应力和应变分布情况.从上面的分析可以看出两组丝锥的最大应力值均小于丝锥材料250 MPa的许用应力值.由于两组丝锥的最大应变都非常小，所以我们只对两组丝锥的应力进行分析.

从图5(a)、(c)、(e)中可知，原成组等径直槽丝锥粗、中锥的最大应力都集中在容屑槽上，最大应力值分别为12.43 MPa和20.19 MPa.原成组等径直槽丝精锥的最大应力点在第二个切削齿处，为28.67 MPa.从图5(b)、(d)、(f)中可知优化后成组不等径直槽丝锥锥头、中锥的最大应力都集中在容屑槽上，最大应力值分别为10.16 MPa和15.39MPa.优化后成组不等径直槽丝锥精锥的最大应力点在第三个切削齿处，为19.67 MPa.

图5 不等径丝直槽丝锥应力云图

原成组等径直槽丝锥粗、中锥的最大应力都集中在容屑槽上，并且云图所对应的色块面积大.这是因为粗、中锥的攻丝扭矩大，丝锥容易在中间部位发生扭断.而优化后成组不等径直槽丝锥粗、中丝锥的最大应力也分布在容屑槽上，但应力分布均匀，云图所对应的色块面积较小，这就说明粗、中锥的切削负荷分配合理，扭矩较小.原成组等径直槽丝锥精锥在切削齿上应力分布不均匀，有应力集中现象，并且应力较大.而优化后成组不等径直槽丝锥精锥在切削齿上应力分布均匀，应力较小.应力集中是导致刀齿损坏变形的主要原因.因此，优化后成组不等径直槽丝锥精锥满足攻丝时的强度要求.

5 结论

通过对1 1/4-7UNC成组不等径直槽丝锥几何参数进行合理的优化设计，并对丝锥有限元模型进行合理的施加载荷，通过有限元软件进行静力分析来验证丝锥的合理性，这种方法是切实可行的.从仿真结果中可以看出优化后成组不等径直槽丝锥的应力的大小及其分布情况十分合理，并且加工出的螺纹表面粗糙度好，精度高，使用寿命长.

[1]程龙.典型难加工材料用修正齿丝锥槽形参数专用化研究[D]. 哈尔滨：哈尔滨工业大学，2010.

[2]韩荣第，杨荣福，李秀英.钛合金攻丝扭矩和切削温度的研究[J].哈尔滨工业大学学报，1985(A6)：146-153.

[3]杨钟祺.成组不等径丝锥设计的新方法[J].工具技术，1999(7):18-20.

[4]姚建平.整体硬质合金螺旋槽丝锥的结构分析[D].成都：西华大学，2010.

[5]金剑.大螺距螺旋槽丝锥的优化设计及有限元分析[D]. 柳州：广西工学院，2012.

[6]徐有仓.装配式成组不等径内容屑丝锥的设计[J].工具技术，2010(12)：75-77.

[7]韩荣第，宋孝宗.螺旋槽丝锥的有限元分析及其结构设计[J].工具技术，2007(41)：41-43.

[8]韩荣第，桂刚.基于有限元的内容屑丝锥结构设计[J].工具技术，2006(40)：25-27.

Design Optimization and Finite Element Analysis of Unequal Serial Straight Slot Taps

WANG Xiaoyu, ZHANG Yang, LI Ronghua, ZHOU Ying

(School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116021,China)

It is hard to perform tapping processing steps using universal serial taps owing to high strength and toughness of hard metal materials. The article aims to problems such as big torque, easy to break and low accuracy of machined thread when processing hard metal materials using 1 1/4-7UNC. In order to solve the technical problem, unequal-diameter structure is designed based on force and torque analysis of serial tap tapping. To reduce the tapping torque and improve processing accuracy, the geometric parameters are better designed, and a three-dimensional model of two taps is established. The finite element analysis of the model shows that the optimized tap structure is more reasonable. Besides, the surface, accuracy and service life of the thread machined by the optimized taps are better.

hard metallic materials; unequal serial straight slot taps; finite element analysis

1673- 9590(2016)06- 0072- 04

2016-05-10

王晓煜(1979-),男，副教授，博士，从事机械电子工程的教学的研究E- mail:99925010@qq.com.

A