基于铣削稳定性的淬硬钢铣削加工工艺参数优化
姜彦翠,刘献礼,吴石,李荣义,王洋洋
(哈尔滨理工大学 机械动力工程学院,黑龙江 哈尔滨 150080)*
基于铣削稳定性的淬硬钢铣削加工工艺参数优化
姜彦翠,刘献礼,吴石,李荣义,王洋洋
(哈尔滨理工大学 机械动力工程学院,黑龙江 哈尔滨 150080)*
针对淬硬钢在铣削加工过程中易发生颤振的问题,建立了淬硬钢铣削过程稳定性预测模型,得到铣削过程稳定性极限曲线图,并同步预测表面动态加工误差,以此作为铣削加工工艺参数优化的约束条件,以主轴转速、每齿进给量、轴向切深工艺参数为设计变量,以最大材料去除率和表面粗糙度为目标函数,进行淬硬钢铣削加工工艺参数优化,并进行铣削实验对比分析,结果表明该方法可以降低铣削过程振动幅值,提高加工效率.
淬硬钢;铣削稳定性;工艺参数优化
0 引言
近年来,随着模具、航空航天、化工、冶金和食品等工业的快速发展,淬硬钢材料已得到广泛应用. 淬硬钢材料属于典型高硬度、高强度材料,淬火后硬度达到HRC45-65[1],铣削加工系统相对而言为柔性系统,且铣削加工过程中铣削力变化大,因此易发生颤振,这是导致工件表面品质恶化的主要原因之一. 若对加工工艺系统动态性能和铣削过程动力学特性了解不清,铣削加工工艺参数选定不合理,无法有效的控制颤振,则导致工件加工表面恶化. 一些企业为了避免淬硬钢铣削过程颤振的发生,通常以牺牲加工效率为代价,选择保守的切削参数,导致数控加工设备性能得不到充分发挥,加工效率降低. 在有效控制淬硬钢铣削过程颤振的基础上,尽可能的发挥加工工艺系统效能,则需要对铣削加工工艺参数进行优化.
国内外一些学者对淬硬钢铣削工艺参数优化的研究主要是用试验优化方法、试验优化与算法优化组合方法,主要是以切削速度、进给量、切削深度等主要切削参数为设计变量,优化目标主要为切削力、加工效率、刀具磨损寿命、表面粗糙度、加工成本等,在铣削试验基础上采用优化算法建立仿真模型,找到切削参数的最佳搭配. Suresh N等[2]提出了将遗传算法与正交试验组合,优化目标为表面粗糙度,进行切削参数优化及刀具形状优选研究. 李占杰[3]进行淬硬钢正交试验研究,对切削力和表面粗糙度两个指标进行优化,采用综合平衡法确定出一组最优方案. 王成勇等[4-5]分析了切削刀具、加工工艺参数和走刀方式等对铣削淬硬模具钢加工过程的影响,提出了改善加工条件和提高加工质量的方法. 何宁等[6]通过大量试验以表面粗糙度和切削力为目标进行了刀具角度和铣削用量等参数的分析和优化研究. 可以看出,这些研究成果对于对于淬硬钢铣削加工工艺参数优化具有重要意义,但是以有效控制铣削过程颤振,保证铣削过程稳定性的角度出发进行的工艺参数优化研究相对较少.
本文以主轴转速、每齿进给量、轴向切深等工艺参数为设计变量,以最大材料去除率和表面粗糙度为优化目标函数,以淬硬钢铣削过程稳定性、动态加工位置误差、刀具变形等作为约束条件,进行淬硬钢切削工艺参数优化.
1 约束条件
1.1 淬硬钢铣削过程稳定性约束条件
本文淬硬钢铣削过程稳定性分析是基于前期主轴系统动力学特性分析结果[7],采用Alintas和Budak提出的切削稳定性分析模型,即频域法,随时间变化的动态铣削过程的铣削力系数模型采用傅立叶展开形式近似.
铣削颤振稳定域预测的主要过程如下:利用有限元法获得主轴系统的传递函数;建立动态铣削力模型;在主模态附近选择颤振频率;建立特征方程并求解;计算临界轴向切深;对于每个稳定性叶瓣计算主轴转速;在一定颤振频率范围重复上述计算,即可绘制出铣削系统稳定性叶瓣图,其计算流程如图1所示,淬硬钢动态铣削过程模型如图2所示,将加工工艺系统简化为x向和y向的二自由度系统.
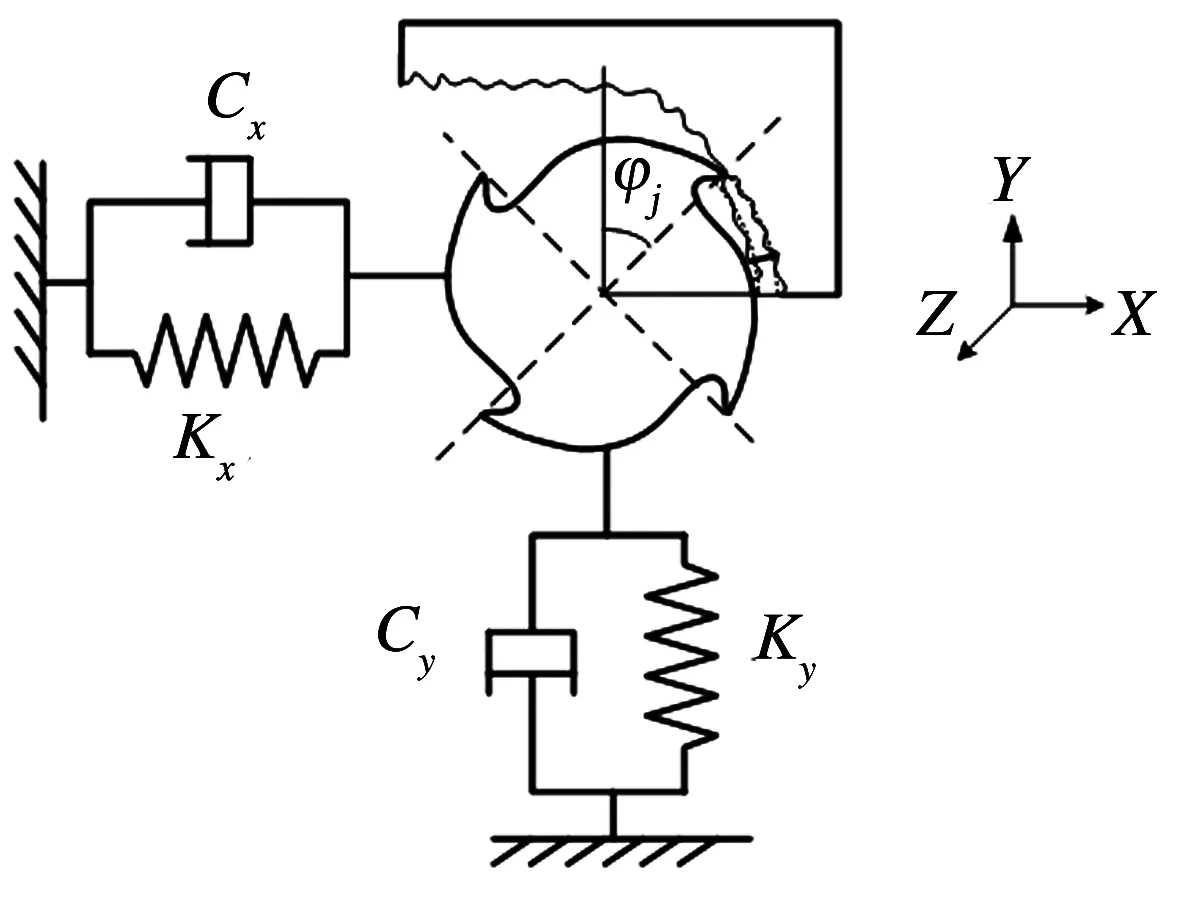
图1 铣削稳定域预测流程

图2 动态铣削过程模型
主轴系统传递函数可表示为刀尖点位移的傅立叶变换X(jω)与刀尖点的动态铣削力的傅立叶变换F(jω)之比,如式(1)所示. 极限轴向切深与主轴转速的计算公式如式(2)、式(4)所示.
(1)
(3)
(4)
其中,k=(0, 1, 2,…),表示稳定域叶瓣数.
1.2 动态加工误差约束条件
为保证淬硬钢表面加工精度的要求,在考虑铣削系统颤振稳定域同时,应考虑在稳定域内铣削的表面位置误差,即铣削系统颤振稳定域和表面位置误差同步预报.
在铣削稳定性分析时建立动态铣削力模型的基础上,利用傅立叶变换得到动态铣削力在频域的表达形式;然后基于有限元法分析得到的刀尖频响函数,计算得到刀尖的位移;接着通过逆傅立叶变换即可得到时域的刀尖位移.
1.3 工艺参数限制约束
(5)
式中,fzmax、fzmin为机床允许最大每齿进给量和最小每齿进给量,apmax、apmin为机床允许最大轴向铣削深度和最小轴向铣削深度,nmin、nmax为主轴最大转速和最小转速.
2 目标函数
2.1 材料去除率
在淬硬钢铣削加工过程中,通过合理选择铣削工艺参数,可以有效控制铣削颤振,实现无颤振稳定铣削高效铣削加工. 本文考虑到淬硬钢铣削过程中的表面加工质量和加工效率的要求,选定了材料去除率MRR和表面粗糙度Ra两个目标函数. 其中MRR定义如下:
MRR=ap×ae×n×fz×N
(6)
2.2 表面粗糙度
表面粗糙度是已加工表面质量的基本表征指标,对工件的使用性能有很大的影响. 铣削加工时,表面粗糙度的表达式为:
(7)
式中,fz为每齿进给量,v为进给速度,ap为轴向铣削深度,ae为径向铣削深度,CRa、c1、c2、c3、c4为常系数.
2.3 综合目标函数
(8)
式中λ1、λ2分别为权重系数,反应材料去除率和表面粗糙度的重要程度,Ra0、MRR0为优化前的表面粗糙度和材料去除率.
3 优化算法
本文采用的优化算法为粒子群优化算法,该方法是一种群体优化算法,与其他优化算法相比,粒子群优化算法具有在优化开始进行初始化时,各粒子在其存在区域内都有自己的位置和速度的特点. 具有进化特征,通过粒子在自己区域寻找最优值和全局最优值实现的,这一特点使粒子群算法具备局部检索最优值的能力外,同时具备寻找全局最优值的能力,是一种并行优化算法.
在每一代的优化过程中,粒子根据式(9)来更新自己的速度和位置.
(9)
式中,w为惯性权因子,c1,c2为正数的学习因子,r1,r2为0~1之间的任意随机数.
由于本文设置的决策变量为主轴转速、进给量和轴向切深,因此,设定粒子维数为3. Xi=[xi1,xi2,xi3],Vi=[vi1,vi2,vi3]. 铣削工艺参数优化问题是包含了多个非等式约束,采用罚函数法对约束进行处理,在目标函数上附加惩罚项,对违反约束的点进行惩罚,从而将有约束问题转化为无约束问题. 粒子的搜索区间范围如式(5)所示.
4 优化过程与结果
笔者前期对主轴系统动力学特性进行了预测与分析,已获得了主轴系统的相关模态参数和传递函数[5],在此基础上通过频域法进行淬硬钢铣削过程稳定性预测获得淬硬钢铣削稳定性极限曲线图如图3所示.
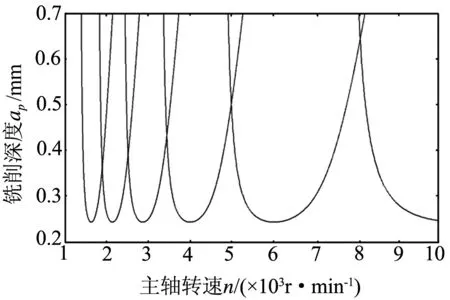
图3 淬硬钢铣削稳定性极限曲线
在建立淬硬钢铣削稳定性模型的基础上,进行表面动态加工误差的同步预测,其预测结果如图4所示.

图4 表面位置误差
淬硬钢铣削加工设备采用大连VDL-1000E型立式数控加工中心,工件材料为Cr12MoV,铣削加工选用硬质合金球头铣刀,其刀具直径为20mm,刀齿数为2.
在使用粒子群优化算法的优化过程中,粒子的参数设置直接决定优化结果性能. 粒子的参数主要是初始粒子数a选择为60,惯性权因子w选为1,学习因子c1、c2范围在0~ 4之间,本文取c1=c2=2,迭代次数n选择200. 通过matlab编写参数优化程序,得到铣削工艺参数优化结果如表1所示[8].
表1 铣削工艺参数优化

主轴转速/(r·min-1)每齿进给量/mm径向切深/mm轴向切深/mm材料去除率/(mm3·min-1)原工艺参数40000.350.40.3336优化后工艺参数60000.40.40.2374
进行淬硬钢铣削加工对比实验,数据采集分析系统选用东华DH5922信号采集系统,采样频率为5 kHz;信号采集选用PCB加速度传感器,其灵敏度是10.42 mv/g. 分别以原工艺参数和优化后工艺参数进行铣削加工,并对比分析加工过程铣削过程和铣削结果. 工艺参数优化后,材料去除率提高了11.3%. 铣削过程振动对比见图5和图6所示,铣削最大振动幅值由原工艺参数下的9.8 m/s2降低为优化工艺参数后的5.7 m/s2. 通过铣削加工工艺参数优化,淬硬钢工件表面质量有所改善,且加工效率也有所提高.

(a) 切削振动信号
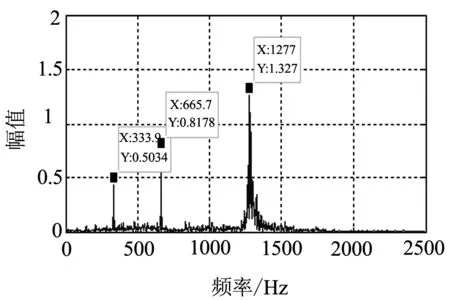
(b) 振动信号的频谱分析
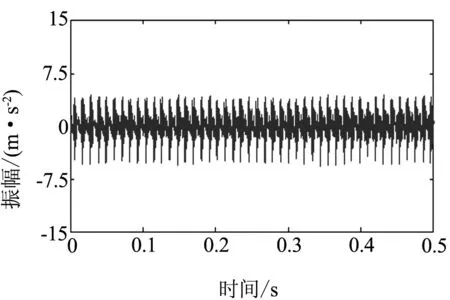
(a) 切削振动信号
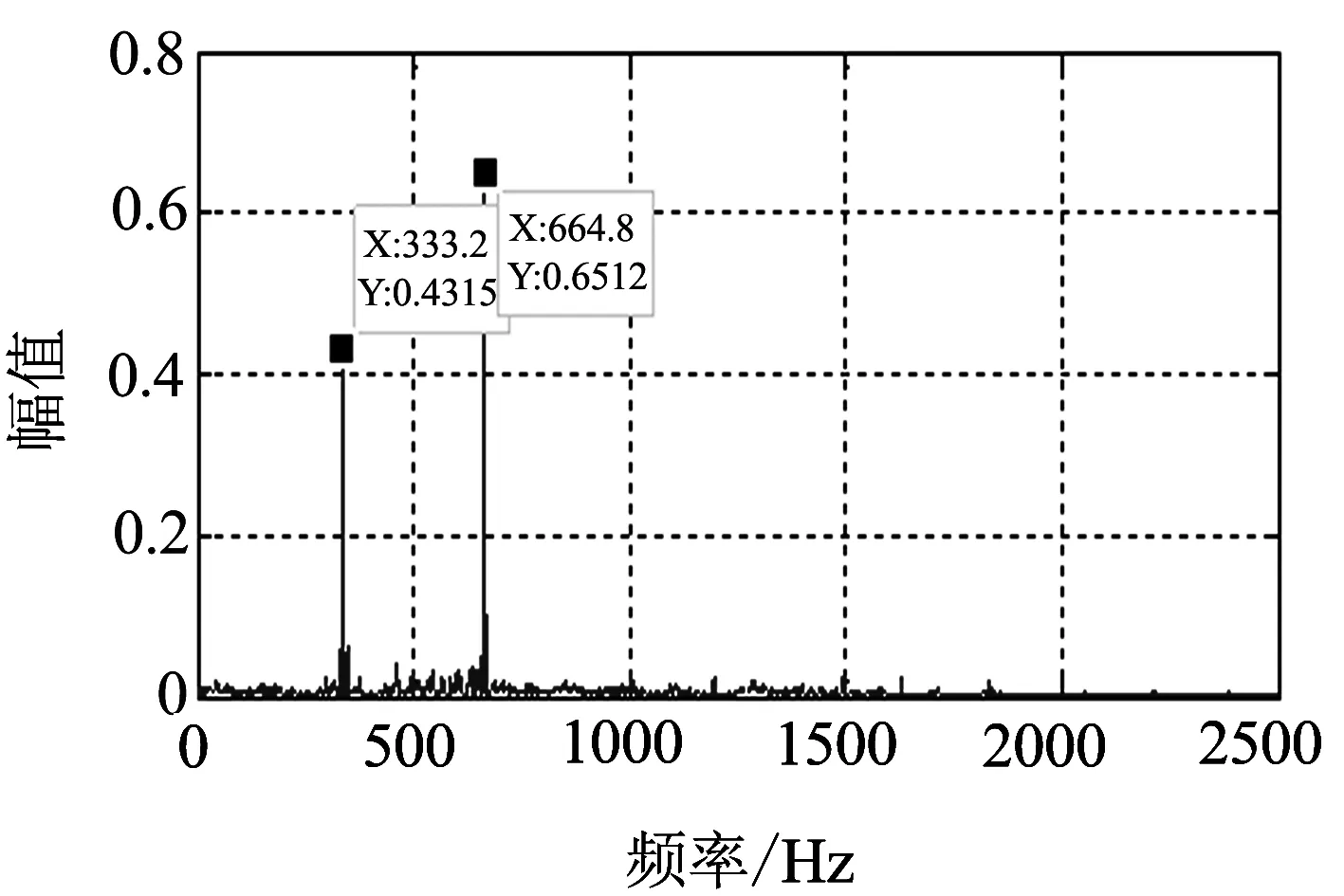
(b) 振动信号的频谱分析
5 结论
淬硬钢由于工件材料硬度高,铣削加工系统相对而言为柔性系统,且铣削加工过程中铣削力变化大,因此易发生颤振. 本文基于淬硬钢铣削过程稳定性预测进行加工工艺参数优化,旨在合理选定工艺参数,有效控制颤振. 通过频域法建立铣削稳定性预测模型得到铣削稳定性极限曲线图,并同步预测工件表面动态加工误差. 以铣削稳定性、动态加工位置误差、工艺参数限制等作为约束条件,以主轴转速、每齿进给量、轴向切深等工艺参数为设计变量,以最大材料去除率和表面粗糙度为优化目标函数,进行淬硬钢铣削加工工艺参数优化. 并通过铣削对比实验进行分析,可以看出以优化后的加工工艺参数进行铣削加工,降低了铣削加工振动幅值,提高了表面质量和加工效率.
[1]ALTAN T,LILLY B,YEN Y C,et al. Manufacturing of dies and molds[J]. Annals of the CIRP,2001,50(2):404- 422.
[2]SURESH N,KUMAR REDDY, VENKATESWARA RAO P.Selectionof an optimal parametric combination for achieving a better surface finish in dry m illing using genetic algorithms[J]. International Journal of Advanced Manufacturing Technology,2006(28):463-473.
[3]李占杰. 淬硬钢高速铣削参数优化试验研究[J]. 现代制造工程, 2006 (7):9-11.
[4]全燕鸣,王成勇,林金萍.高速铣削淬硬模具钢的工艺性与经济性研究[J]. 工具技术,2003,12:6-8.
[5]周树锦.淬硬钢模具高速铣削工艺参数优化研究[D]. 广州:广东工业大学,2007.
[6]IQBAL A,HE N,LI L,DAR N. A fuzzy expert system for optimizing parameters and predicting performance measures in hard-milling process[J]. Expert Systems with Applications, 2007,32:1020-1027.
[7]姜彦翠,刘献礼,吴石,等. 考虑结合面和轴向力的主轴动力学特性[J]. 机械工程学报,2015,51(19):66-74.
[8]郝洪艳, 汤文成, 王保升. 基于铣削力与稳定性预测的铣削工艺参数优化[J]. 组合机床与自动化加工技术, 2013(10):43- 46.
Optimization of Milling Process Parameters for Hardened Steel Considering Milling Stability
JIANG Yancui, LIU Xianli, WU Shi, LI Rongyi, WANG Yangyang
(School of Mechanical and Power Engineering, Harbin University of Science and Technology, Harbin 150080, China)
Aiming at the fluttering of hardened steel milling process, the milling stability prediction model is established to obtain the milling stability lobes. Considering dynamic surface machining error as a milling process parameter optimization constraint and taking spindle speed, feed rate per tooth and axial depth of cut process parameters as design variables, the maximum material removal rate and surface roughness of the objective function, the optimization of the milling process parameters for hardened steel are theoretical analyzed and verified by milling experiments. The experimental results show that this method can reduce the vibration amplitude of the milling process and improve processing efficiency.
hardened steel; milling stability; process parameters optimization
1673- 9590(2016)06- 0026- 05
2016-06-01
国家自然科学基金重点项目(51235003)
姜彦翠(1984-),女,讲师,博士,主要模具加工系统动力学研究,铣削过程动力学的研究
A
E- mail:jiangyancui@hrbust.edu.cn.

