卫星导航干扰信号波达方向估计分析*
朱银兵,李 豹,刘敬虎,曹可劲
(1 海军工程大学电气工程学院,武汉 4300331;2 91576部队,浙江宁波 315000)
卫星导航干扰信号波达方向估计分析*
朱银兵1,李 豹1,刘敬虎2,曹可劲1
(1 海军工程大学电气工程学院,武汉 4300331;2 91576部队,浙江宁波 315000)
为提高卫星导航系统波达方向估计能力,利用功率倒置、空时联合滤波、MUSIC及其改进算法分别在干扰信号波达方向独立和相关条件下对比分析其波达方向估计能力。结果表明,波达方向独立时,功率倒置和空时联合滤波算法存在2°~3°估计偏差,而MUSIC及其改进算法能够准确估计;波达方向相关时,MUSIC和空时联合滤波算法失效,功率倒置法难以区分相关干扰信号,而MUSIC改进算法的估计误差为2°,可大幅提升波达方向估计准确性。
卫星导航;干扰;波达方向;功率倒置;空时联合滤波;MUSIC
0 引言
卫星导航的干扰信号主要包括压制和欺骗干扰信号两种,欺骗干扰信号功率通常与真实信号相近,而且实施欺骗干扰的同时一般伴随有压制预先干扰。因此,卫星导航干扰信号的估计通常针对研制干扰展开研究。目前,在工程领域通常采用最小均方、递推最小二乘、采样矩阵求逆和Howells-Applebaum[1]等自适应算法进行压制干扰抑制,但是这些算法计算量大。此外,在自适应算法中,一般需要选择一个合适的信号作为期望信号,然而到达地球表面的卫星导航信号十分微弱,而且可能受到多个且方向并不确定的干扰。在这种条件下,利用线性约束最小方差(LCMV)准则,在最小方差准则的前提下,调整自适应算法权系数至最佳使阵列输出噪声方差最小的功率倒置算法[2-3]和基于线性约束的空时联合滤波(space-time least-mean-square, STLMS)算法[4-6]具有很强的实际应用价值。这两种方法尤其是前一种方法已经得到了工程应用,对压制干扰具有较好抑制效果,但是在阵元数量和分布一定,且多个干扰信号相关性较强时,由于线性约束条件的引入,使得估计得到的干扰信号波达方向(direction of arrival, DOA)误差增大,有必要借助其他估计方法获得更高的估计精度。为此,文中引入基于噪声子空间估计的多重信号分类(multiple signal classification, MUSIC)方法[7-9]进行比对分析,以提高卫导系统对波达方向相关干扰的识别能力。
1 天线阵模型
文中分析采用“Y”型天线阵模型,如图1所示。令各阵元在水平面内与x轴所成张角为φm(m=2,3,4)。圆的半径r小于或等于卫星信号半波长,信号S(t)到达方位角和俯仰角分别为θ和φ,则信号S(t)的方向矢量a(θ,φ)为:

(1)

图1 天线阵模型
假设有P个卫星信号Sp和Q个干扰信号Jq同时入射到天线阵列,则阵元在某个采样时刻n的输出信号为:
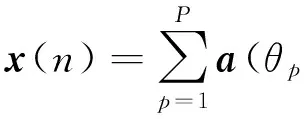

(2)
式中:A=[a(θ1,φ1),a(θ2,φ2),…,a(θP+Q,φP+Q)];S(n)=[S1(n),…,SP(n),JP+1(n),…,JP+Q(n)];n(n)为热噪声,功率为σ2。
2 算法原理
2.1 功率倒置算法


图2 功率倒置算法
根据功率倒置算法约束条件wHs=1,经推导可得其权值递推公式为[3]:
(3)
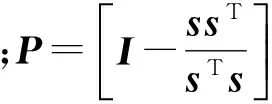
y(n)=wH(n)x(n)
(4)
2.2 空时联合滤波算法
空时处理模型通常也称为FROST阵列模型,由于自由度大量增加,可显著提升干扰抑制效果。文中引入原理相对简单且不需要进行输入信号相关矩阵计算和矩阵求逆运算的空时最小均方算法[1](STLMS)展开分析。该算法首先计算线性滤波器输出对输入信号响应,并得到估计误差,然后根据估计误差自动调节滤波器权值。算法展开模型如图3所示。

图3 STLMS算法处理模型
令基本信号为d(n),M个辅助通道各包含一组N阶横向滤波器,则输入为:
x(n)=[x1(n),…,x1(n-N+1),x2(n),…,
x2(n-N+1),…,xM(n),….xM(n-N+1)]T=
(5)
令权值矢量为w=[w1(0),w1(1),…,w1(N-1),w2(0),w2(1),…,w2(N-1),…,wM(0),wM(1),…,wM(N-1)]T,则可推导得该算法权值递推公式为[1]:
ω(n+1)=ω(n)+2μ(rxd-Rxxω(n))=
[I-2μx(n)xH(n)]ω(n)+2μx(n)d*(n)
(6)
其中μ为步长因子。同理可由式(4)求解STLMS算法输出。
2.3 MUSIC改进算法
假设有L个信号入射到M阵元的阵列天线上,则接收信号为:

(φi)si(t)+n(t)=As(t)+n(t)
(7)
式中:x(t)为含噪声信号矢量;s(t)为信号矢量;n(t)为噪声矢量;a(φi)表示第i个信号对应的阵列方向矢量,φi为波达方向仰角。
对MUSIC算法给定阵列信号模型,假设对于不同的φi,a(φi)线性独立,噪声为复高斯白噪声,且相关矩阵Rxx是非奇异的。则对其协方差矩阵进行特征值分解可得Rxx的特征值为Λ=diag{λ1,λ2,…,λL,λL+1,λL+2,…,λM}。其中,前L个较大的特征值λ1,λ2,…,λL定义为信号特征值,λL+1,λL+2,…,λM定义为噪声特征值。在实际处理过程中,特征值通常满足λ1>…>λL>λL+1>λL+2>…>λM=σ2,即最小特征值λM必然是噪声特征值[8]。因此,利用Rxx最小噪声特征值对应的特征向量qM构成一维噪声子空间,从而可得改进算法空间谱函数为:

(8)

3 仿真分析
为了分析几种方法在卫星导航信号波达方向估计上的差异,文中假设卫星导航信号以(120°,60°)方向入射到阵面,前者为方位角,后者为仰角(后续表述类似),在信噪比为SNR=-23 dB,信干比为JNR=30 dB条件下,分别利用功率倒置法、空时联合滤波算法、MUSIC及其改进算法在4种不同情况下对干扰信号波达方向进行仿真分析:
情况一:干扰为单个独立信号源,来向为(60°,30°);
情况二:干扰为两个独立信号源,来向分别为(60°,30°)和(100°,65°);
情况三:干扰为3个独立信号源,来向分别为(60°,30°)、(110°,50°)和(160°,60°);
情况四:干扰为两个来向相近的信号源,一组来向分别为(60°,30°)和(62°,30°),另一组来向分别为(60°,30°)和(70°,30°)。
4种情况下的干扰信号波达方向估计结果如表1所示。由表可见,在干扰源相互独立情况下(对应情况一、二、三),4种方法都能够较准的估计出干扰信号波达方向,经比对可以发现,采用功率倒置法和空时联合滤波算法的估计结果有时会产生2°~3°的估计误差,但是采用MUSIC及其改进算都能够准确的估计出干扰信号波达方向;在干扰源具有一定相关性时(情况四),4种方法的估计结果分别如图4~图11所示。
根据图4到图11,在干扰信号波达方向相关时可得以下结论:
1)功率倒置法在干扰信号波达方向接近时估计误差较大;观察图4和图5可见,虽然由零陷最深的点可以估计出干扰源波达方向,但是零点位置连成一片,分别以61°和65°为中心,易被误认为一个干扰源。因此,利用这种算法在处理干扰相关时,干扰源波达方向指示误差增大,不利于使用现有设备对干扰源进行有效定位。

图4 (60°,30°)和(62°,30°)来向的功率倒置法估计
2)空时联合滤波算法在干扰信号波达方向来向接近时估计误差较大;观察图6和图7可见,与功率倒置法类似,空时联合滤波算法虽然由零陷最深的点可以估计出干扰源波达方向,但是零点位置同样连成一片,易被误认为一个干扰源。此外,在干扰来向分别为(60°,30°)和(70°,30°)时仅估计出了前一个干扰信号波达方向,误差显著增大。
3)MUSIC算法在干扰来向分别为(60°,30°)和(62°,30°)时没有估计出干扰信号,在干扰来向分别为(60°,30°)和(70°,30°)时仅估计出了后一个干扰信号波达方向,由此可见,MUSIC算法对相互独立的高干信比卫星导航干扰信号具有较强估计能力,但是对相关干扰信号,估计能力急剧下降。

图5 (60°,30°)和(70°,30°)来向的功率倒置法估计

图6 (60°,30°)和(62°,30°)来向的空时联合滤波算法估计

图7 (60°,30°)和(70°,30°)来向的空时联合滤波算法估计

图8 (60°,30°)和(62°,30°)来向的MUSIC算法估计
4)与MUSIC算法不同,改进算法仅用特征值最小的一维噪声子空间进行估计,在干扰相关时较准确的估计出了两个干扰源信号波达方向;此外,与图4到图7对比可见,虽然估计结果和功率倒置法估计结果一致,但是采用MUSIC改进算法得到的估计结果分辨率更高,能够明显分辨出两个干扰,具有更高实际应用价值。

图9 (60°,30°)和(70°,30°)来向的MUSIC算法估计

图10 (60°,30°)和(62°,30°)来向的MUSIC改进算法估计
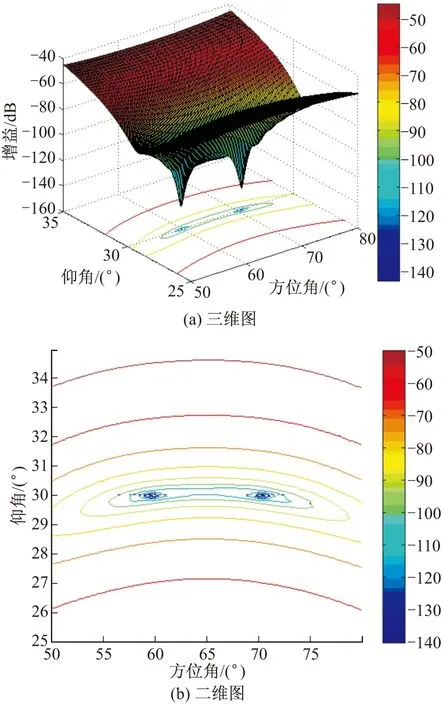
图11 (60°,30°)和(70°,30°)来向的MUSIC改进算法估计

表1 4种情况下干扰信号波达方向估计
4 结论
为了获得高分辨率的卫星导航干扰信号波达方向估计,文中结合卫星导航系统中压制干扰通常比卫星信号功率强得多的特点,在简要介绍功率倒置法、空时联合滤波算法、MUSIC及其改进算法基础上,利用这四种算法在多个干扰信号相互独立和两个波达方向具有一定相关性干扰信号条件下,对干扰信号的波达方向进行仿真分析。结果表明,对相互独立干扰信号,功率倒置法、空时联合滤波算法、MUSIC及其改进算法都能够较准确的估计干扰信号波达方向,但是由于功率倒置法和空时联合滤波算法限定了某一天线阵元权值为1,使得估计结果可能存在2°~3°估计偏差,而MUSIC及其改进算法不存在该问题;对波达方向具有一定相关性干扰信号,MUSIC算法适应性较差,空时联合滤波算法适应性一般,而功率倒置法和MUSIC改进算法都能够较准确的估计干扰信号波达方向,但是与功率倒置法相比,MUSIC改进算法具有更好的估计分辨率,对实际应用过程中干扰源有效定位更具有应用价值。因此,可在接收机中使用功率倒置算法实现压制干扰信号有效抑制,同时采用MUSIC改进算法对干扰信号波达方向进行准确估计,从而有效提升卫星导航系统干扰信号波达方向估计准确度。
[1] 程震. GPS抗干扰调零天线系统信号处理的设计与实现 [D]. 南京: 南京航空航天大学, 2011: 15-18.
[2] 张平平. 北斗导航终端天线与抗干扰算法的研究与实现 [D]. 南京: 南京理工大学, 2014: 39-49.
[3] 苗静. 卫星导航自适应抗干扰算法在FPGA中的实现 [D]. 石家庄: 河北科技大学, 2014: 29-34.
[4] 王立兵, 韩宁, 龚文飞. 可用于快速搜索卫星信号的降维空时波束形成算法 [J]. 南京航空航天大学学报, 2013, 45(3): 402-408.
[5] 梁思远, 王党卫. 卫星导航增强型终端抗干扰技术研究 [C]∥第五届中国卫星导航学术年会电子文集, 2014: 1-5.
[6] 赵军, 于雪岗. 卫星导航STAP算法的低仰角性能研究 [J]. 无线电工程, 2014, 44(1): 46-48.
[7] 苏昭斌, 陈红卫. 基于改进MUSIC算法的雷达海上目标检测 [J]. 科学技术与工程, 2013, 13(31): 9236-9240.
[8] 张俊博. 基于子空间DOA估计方法的研究与应用 [D]. 上海: 复旦大学, 2013: 15-22.
[9] 闫雪梅. 基于平台移动特性提高测向精度算法的研究 [D]. 哈尔滨: 哈尔滨工业大学, 2013: 13-17.
DOA Estimation Analysis for Satellite Navigation Jamming
ZHU Yinbing1,LI Bao1,LIU Jinghu2,CAO Kejin1
(1 College of Electric Engineering, Naval Engineering University, Wuhan 430033, China;2 No.91576 Unit, Zhejiang Ningbo 315000, China)
In order to enhance satellite navigation system’s capability of estimating arrival direction of jamming, power inversion, space-time least-mean-square, multiple signal classification and its improved algorithm were applied to estimate arrival direction of jamming on independent and interrelated jamming respectively. The results show that:under the independent case, estimation error of power inversion and space-time least-mean-square algorithm is 2°~3°, while it is precisely estimated by multiple signal classification and its improved algorithm. Under the interrelated case, multiple signal classification and space-time least-mean-square algorithm are disable, and it is difficult for power inversion algorithm to identify the jamming, whereas, estimation error of the improved multiple signal classification algorithm is 2°which will enhance arrival direction veracity of jamming effectively.
satellite navigation; jamming; DOA; power inversion; STLMS; MUSIC
2015-07-17
朱银兵(1978-),男,湖北黄冈人,讲师,博士,研究方向:无线电/卫星导航。
TN961
A

