近程反导型舰空导弹引战配合延时规律研究

裴 喆,杨志群

(中国人民解放军92941部队,辽宁 葫芦岛 125000)



近程反导型舰空导弹引战配合延时规律研究

裴 喆,杨志群

(中国人民解放军92941部队,辽宁 葫芦岛 125000)

对近程反导型舰空导弹拦截反舰导弹的引战配合延时规律进行了研究。建立了引战配合延时数学模型，仿真分析了目标易损部位、目标速度、弹目交会角、目标方位角和引信起动距离5个弹目参数的不同双参数组合对延时变化规律的影响。结果发现：目标易损部位对延时影响相对较大，易损部位越靠前对延时越不利；目标速度对延时的影响也很大，尤其当引信探测倾角较大，目标分别为亚声速和两倍以上超声速时，延时规律有所不同；弹目交会角、目标方位角和引信起动距离三个交会参数对延时的影响均较大；单参数对延时影响的规律简单，但多参数共同作用对延时影响的规律复杂。

舰空导弹； 反舰导弹； 近程反导； 引信； 引战配合； 延时； 易损性； 弹目参数

0 引言

引战配合延时直接影响舰空导弹引战配合效率、单发杀伤概率，以及武器系统作战效能。引战配合延时规律是舰空导弹设计和靶场飞行试验评估的重要部分。近程反导型舰空导弹的作战使命是严重毁伤来袭反舰导弹，反舰导弹的速度和易损性有特殊性，速度的特殊在于跨度较大，包括亚声速、超声速、高超声速，易损性的特殊是其要害舱段主要集中在前半身的制导控制舱，因此近程反导型舰空导弹引战配合延时规律也具其特殊性。对引战配合延时进行了大量研究，文献[1-3]研究了空空导弹攻击飞机类目标的延时规律；文献[4]研究了反导导弹拦截亚声速巡航导弹的引战配合效率，但上述文献未研究近程拦截反舰导弹时的延时规律。为此本文对舰空导弹近程拦截反舰导弹的引战配合延时随相关弹目参数变化的规律进行了仿真分析。

1 引战配合延时数学模型

因弹目遭遇时间很短，可认为弹目分别作匀速直线运动，故弹目交会可视作面面交会，即弹目分别在两个互相平行的平面内运动[1-2、5]。舰空导弹引信天线主瓣一般为以弹轴为对称轴、倾角为β的空心圆锥体，由文献[1-2、5]建立引战配合延时数学模型如图1所示。图中：导弹在DNQS平面沿DE方向运动，目标在GHIK平面沿FP方向运动。近程反导通常为迎头攻击，当引信处于点D时，引信探测到目标头部点F后起动。过点F作DN的垂直平面FJO与DN交于点O。取点O为坐标原点，ON为Z轴，过点O作平面GHIK的垂线交平面于点J，OJ为Y轴。引信从点D开始经延时τ在点E引爆战斗部，战斗部破片经时间tP沿EP方向飞行到目标某要害点P。

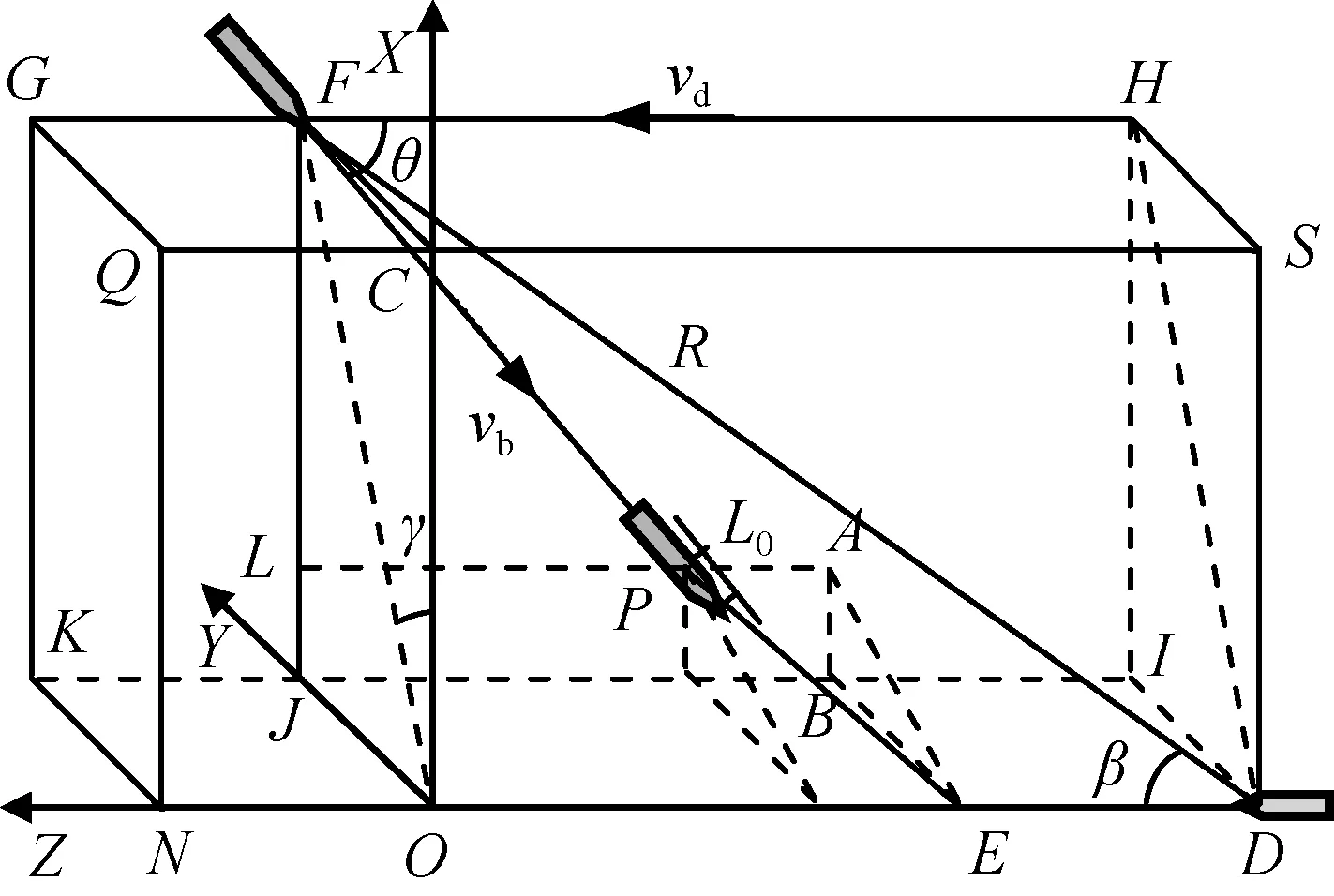
图1 引战配合延时数学模型Fig.1 Mathematical model of delay time of fuze-warhead coordination

由模型几何关系可得

FJ=Rsin βcos γ；

FC=BE=Rsin βsin γ；

AE=v0tp；

FP=vb(τ+tp)-L0；

FL=FPsin θ=[vb(τ+tp)-L0]sin θ.

在直角三角形ABE中，有

{Rsin βcos γ-[vb(τ+tp)-L0]sin θ}2+

(Rsin βsin γ)2=(v0tp)2.

(1)

式中：R为引信起动距离；θ为弹目交会角；γ为目标方位角；β为引信探测倾角；L0为目标的引信起动点至某要害点P的长度(本文称为目标易损部位参数)；tp为战斗部破片从起爆点至击中目标要害点的飞行时间(忽略破片飞行的速度衰减)；vb为目标速度；v0为战斗部破片静态飞散速度(设静态飞散方向与导弹纵轴夹角为90°)；τ为引战配合延时。

因点P是破片击中点，其Z坐标与破片的Z坐标相同，即

-[vb(τ+tp)-L0]cos θ=

vd(τ+tp)-Rcos β-Lm.

式中：Lm为导弹引信中心与战斗部中心间的距离；vd为导弹速度。则

影响立体仓库稳定的主要因素是货架重心高度，两端式同轨双车运行模式较单台堆垛机独立作业模式在货架形式上相差不大，采用式(8)描述的上轻下重原则，目标函数可有效降低货架重心，提升结构稳定性。

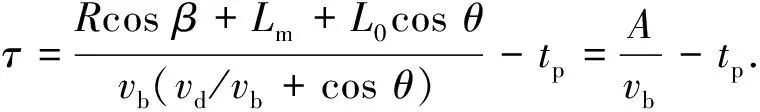
(2)

式中：

A=vb(τ+tp).

(3)

将式(3)代入式(1)，可得

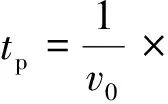
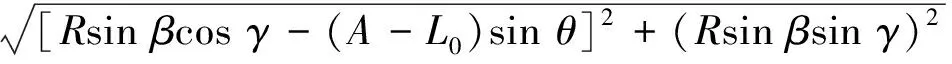
再将tp代入式(2)，即可算得τ。

2 引战配合延时规律仿真与分析

2.1 不同弹目参数的延时仿真结果

由引战配合延时数学模型可知：τ为弹目交会参数和引信战斗部参数的函数；v0，β，Lm，vd均为设计参数，也是可调量，而vb，θ，γ，R，L0随目标类型和弹目交会姿态而变，均是不可调量。模型中未涉及导弹和目标的攻角与侧滑角，这是因为它们对延时的影响可转为θ，γ对延时的影响。因此，本文考虑τ随vb，θ，γ，R，L0这5个弹目参数的变化规律进行仿真。仿真中设v0=2 000 m/s，β=60°，Lm=0.2 m，vd=800 m/s。

在θ=15°，γ=0°，R=3 m条件下，不同vb，L0的τ仿真结果如图2所示。在L0=1 m，R=3 m，γ=0°条件下，不同vb，θ的τ仿真结果如图3所示。在θ=15°，vb=680 m/s条件下，不同γ，R的τ仿真结果如图4所示。在R=3 m，vb=680 m/s条件下，不同γ，θ的τ仿真结果如图5所示。在θ=15°，γ=0°条件下，不同vb，R的τ仿真结果如图6所示。在γ=0°，vb=680 m/s条件下，不同θ，R的τ仿真结果如图7所示。

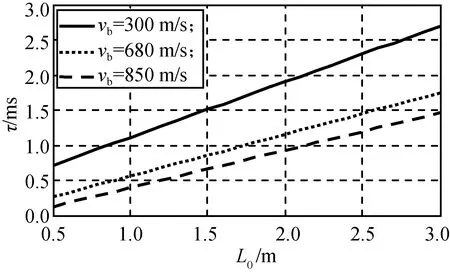
图2 不同L0，vb的τFig.2 τ with various L0 and vb

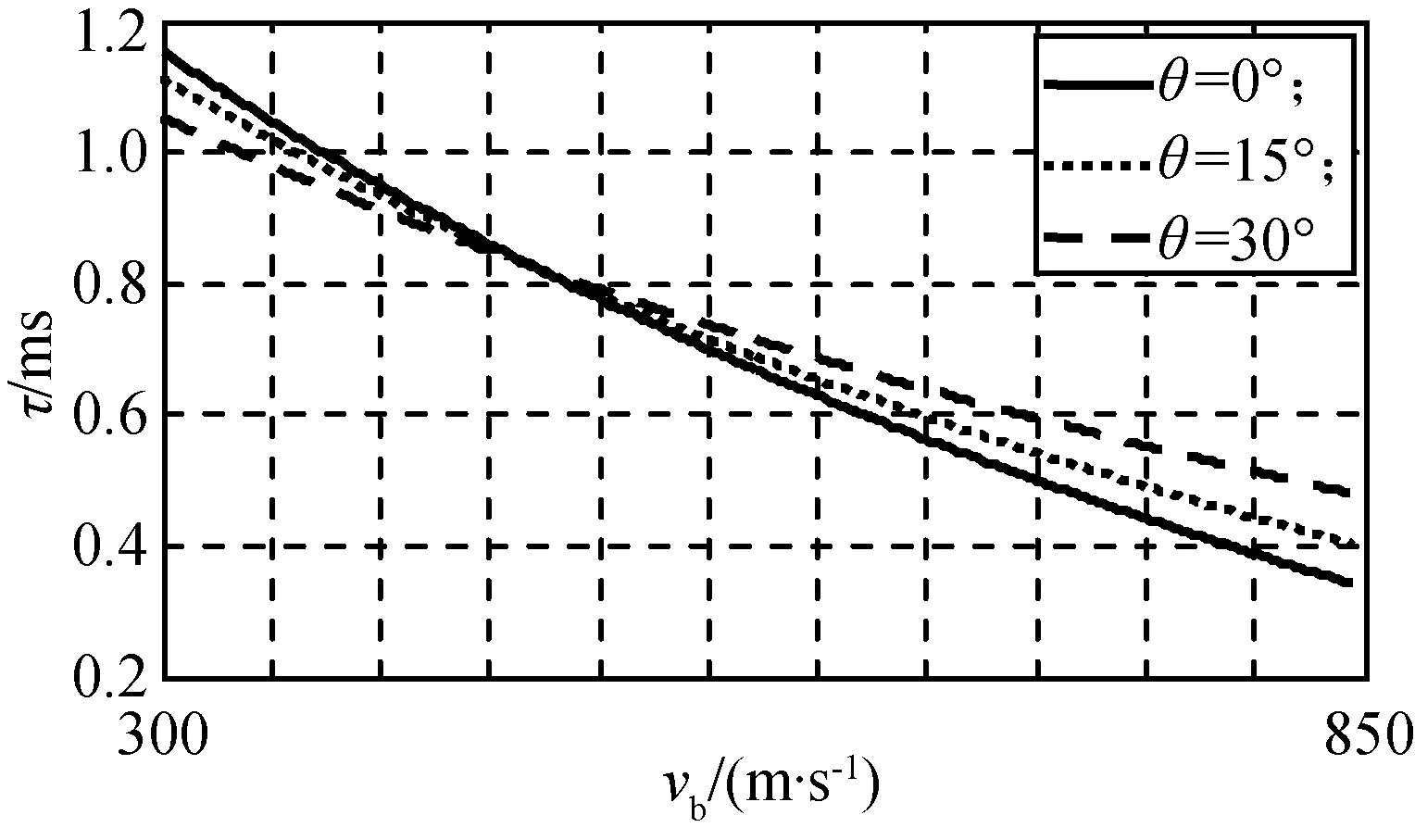
图3 不同vb，θ的τFig.3 τ with various vb and θ

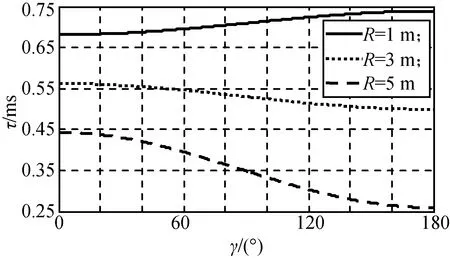
图4 不同γ，R的τFig.4 τ with various γ and R

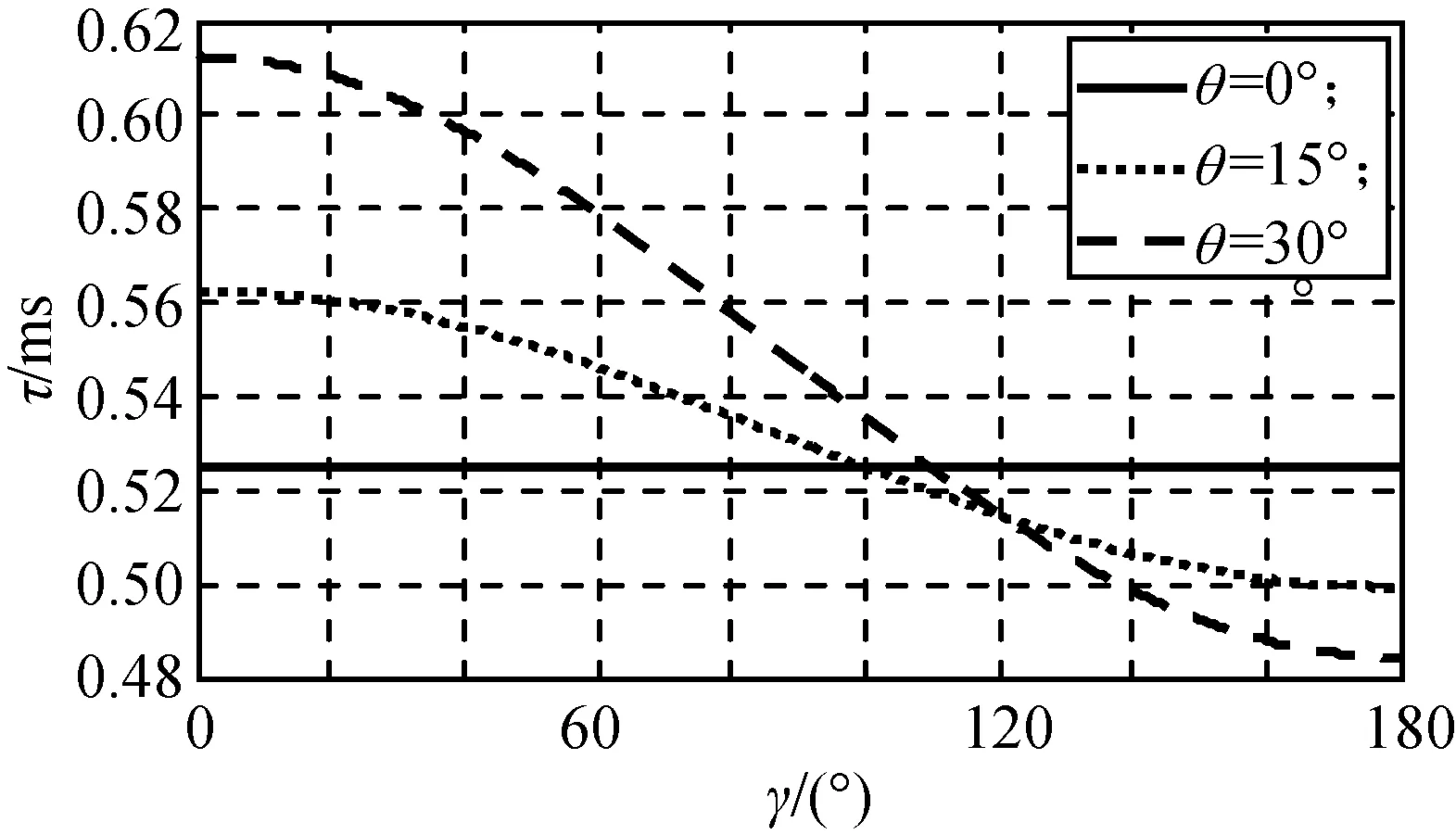
图5 不同γ，θ的τFig.5 τ with various γ and θ

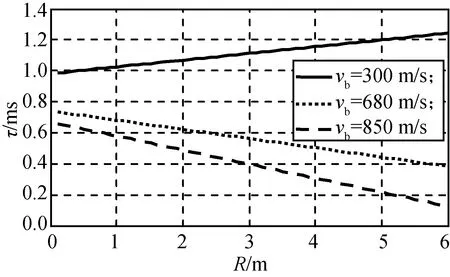
图6 与不同R，vb的τFig.6 τ with various R and vb

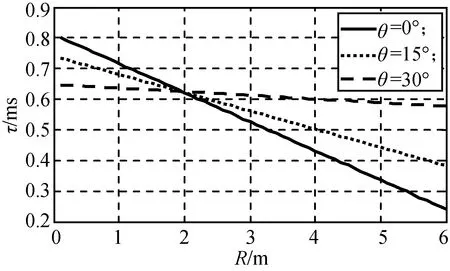
图7 与不同R，θ的τFig.7 τ with various R and θ

2.2 结果分析

反舰导弹易损性与反导作战使命和毁伤模式有关。反舰导弹舱段布局从头到尾通常依次为制导控制舱、战斗部舱、燃料舱和发动机舱。近程拦截应对反舰导弹造成严重毁伤，舰空导弹战斗部破片很难穿透反舰导弹穿甲类战斗部壳体，故反舰导弹严重毁伤模式主要包括空中解体、坠入海水、明显偏航三种[6-7]。近程拦截时反舰导弹一般处于末段飞行弹道，燃料几乎燃烧完，破片即使穿透燃料舱壳体，也很难立即引起严重的功能性毁伤。因此，反舰导弹要害舱段主要集中在破片容易穿透且可能很快引起导弹严重毁伤的制导控制舱，这是本文仿真时L0取值的依据。

由图2 可知：对不同的vb(或弹目相对速度vr)，τ均随L0的增大而增大，但vb或vr较大时增幅较小，因此通过设计调整vd间接增大vr，可减小L0对τ的影响。当R，θ，γ分别取不同值时，τ也总随L0增大而增大。另由图2可知：当L0<0.5 m时τ可能小于0，即目标要害部位越靠前对延时越不利，可见L0对τ的影响很大。由此，引战配合延时设计时须先合理确定其大小，采用破片飞散角不同的双束(或多束)聚焦战斗部可减小无法获取L0对引战配合不利的影响[8]。

2.2.2τ随vb的变化规律

由图2、3、6可知：其他参数不变，vb在0.9Ma～2.5Ma范围内变化时，τ随vb增大而减小。由图6可知：在vb分别为0.9Ma和不小于2Ma两种情况下，不仅τ值大小差别较大，而且τ值随R的变化规律也明显不同。该变化规律不是由R影响产生的，而是由vb，β共同影响形成的。当vb增大为2Ma时，vr已增大至与v0接近，若同时β较大，则留给破片飞行的时间大幅减小，所需τ也随之减小。由此，可认为vb对τ的影响很大，这与文献[9-10]的结论一致。为减小vb对τ的影响，应先提高舰空导弹本身或武器系统实时获取vb的精度，其次可在导弹设计时减小β或增大v0。

2.2.3τ随θ的变化规律

拦截末端机动较小的反舰导弹时，θ一般较小，本文假设其不大于30°。由图3、5、7可知：当vb，γ或R变化时，τ随θ的变化规律不是单调增大或减小。图3中，当vb约为1Ma时，τ随θ的增大而小幅减小；当vb大于2Ma时，τ随θ增大而小幅增大。由此，可认为θ对τ的影响较大。为减小θ对τ的影响，应使导弹在飞行中准确获取θ，另可通过导弹制导控制规律设计将弹目遭遇段的θ控制在较小范围内。

2.2.4τ随γ的变化规律

由图4、5可知：τ与γ的关系类似正弦规律变化。对不同的θ或R，τ随γ的变化规律和幅度差别较大，表明γ对τ的影响也较大。为减小γ对τ的影响，常用多方位探测体制引信(如激发引信)实时测量γ，或用导引头方位探测信息估计得到γ。

2.2.5τ随R的变化规律

由图4、6、7可知：对不同的γ，vb或θ，τ随R的变化规律为线性增大或减小，变化幅度与γ，vb或θ均有关。R可由引信测量获得，故常根据R变化范围设计分档延时。

3 结束语

本文根据舰空导弹近程反导作战的特殊性，对引战配合延时随相关弹目参数的变化规律进行了仿真研究。结果发现：第一，目标易损部位对延时影响很大，易损部位越靠前对延时越不利。由于不同类型反舰导弹的易损部位存在差别，可采用多束聚焦战斗部、增大遭遇段导弹速度等措施减小其对延时的影响。第二，目标速度对延时的影响亦很大，尤其当引信探测倾角较大，目标分别为亚声速和两倍以上超声速时，延时规律不同。为减小目标速度对延时的影响，应提高导弹武器系统测量或获取目标速度的精度，也可由设计减小引信探测倾角或增大战斗部破片静态飞散速度。第三，弹目交会角、目标方位角和引信起动距离三个交会参数对延时的影响均较大，应由引信设计或充分利用导引头信息等方法提高获取此三个参数的能力及精度。第四，单个弹目参数对延时影响的规律简单，但多个参数共同作用对延时造成的综合影响较复杂，引信对这些参数的获取越全面、越准确，延时就越精确。本文研究可用于靶场飞行试验引战配合分析评估，也能为引战配合设计与工程实现提供参考。

[1] 朱景伟, 王瑞刚, 胡昌振. 定向战斗部最佳起爆延迟时间及起爆方位变化特性研究[J]. 探测与控制学报, 1999, 21(3): 26-29.

[2] 张祥金, 冯颖. 定向起爆部脉冲激光方位探测引信系统时间空间匹配特性[J]. 强激光与粒子束, 2011, 23(12): 3197-3202.

[3] 朱景伟, 谭惠民, 樊印海. 求解定向战斗部最佳起爆延迟时间和起爆方位的一种方法[J]. 宇航学报, 2003, 24(2): 198-201.

[4] 李向东, 唐晓斌, 董平. 破片式反导导弹引战配合仿真与效率计算[J]. 上海航天, 2006, 23(3): 11-15.

[5] 张合, 张祥金. 脉冲激光近场目标探测理论与技术[M]. 北京: 科学出版社, 2013: 153-160.

[6] 周智超. 预制破片弹对反舰导弹易损性的技术分析与计算[J]. 弹箭与制导学报, 2006, 26(1): 750-752.

[7] 李向东, 苏义岭, 韩永要. 导弹目标在破片式战斗部作用下的易损性评估[J]. 爆炸与冲击, 2007, 27(5): 468-472.

[8] 何广军, 高福利, 刘彤. 多束破片聚焦式杀伤战斗部毁伤目标的仿真[J]. 爆炸与冲击, 2000, 20(2): 131-136.

[9] 陆永红. 舰空导弹武器系统的引战配合研究[J]. 海军航空工程学院学报, 2001, 16(2): 251-253.

[10] 刘腾谊, 陈佳音, 张安民. 防空导弹自适应起爆延时控制技术研究[J]. 弹箭与制导学报, 2010, 30(1): 143-145.

Delay Time Law Study of Fuze-Warhead Coordination of Short-Range Anti-Missile Ship-to-Air Missile

PEI Zhe, YANG Zhi-qun

(The Unit 92941 of CPLA, Huludao 125000, Liaoning, China)

The delay time law of fuze-warhead coordination of short-range ship-to-air missile intercepting anti-ship missile was studied in this paper. The mathematic model of delay time of fuze-warhead coordination was established. The effect of different dual parameters combination of five parameters which were target vulnerability distribution, target speed, missile-target encounter angle, target azimuth angle and fuze starting distance on the laws of delay time were simulated. The simulation results showed that the influence of target vulnerability distribution on delay time was more serious. The more ahead of the target vulnerability, the worse for the delay time. The influence of target velocity was important. The delay time law would be different especially for search inclination of fuze was large and target flight with subsonic or 2 times sonic above respectively. The influence of the 3 parameters which were missile-target encounter angle, target azimuth angle and fuze starting distance on delay time was large. The effect of single parameter on the law was simple but the comprehensive influence of several parameters was complicated.

Ship-to-air missile; Anti-ship missile; Short-range anti-missile; Fuze; Fuze-warhead coordination; Delay time; Vulnerability; Missile target parameter

1006-1630(2016)04-0108-04

2015-12-24；

2016-03-14

裴 喆(1979—)，男，硕士，主要研究方向为导弹引战系统试验鉴定。

TJ43； TJ761.7

A

10.19328/j.cnki.1006-1630.2016.04.018