低数据率与低阵元数时LCMV和LCEC波束形成算法研究

陆 加,李贝贝,杨革文,陈朝焰

(1.上海机电工程研究所,上海 201109； 2.南京理工大学 电子工程与光电技术学院,江苏 南京 210094)



低数据率与低阵元数时LCMV和LCEC波束形成算法研究

陆 加1,李贝贝2,杨革文1,陈朝焰1

(1.上海机电工程研究所,上海 201109； 2.南京理工大学 电子工程与光电技术学院,江苏 南京 210094)

研究了低数据率与低阵元数条件下应用线性约束最小方差算法(LCMV)算法和线性约束特征干扰相消器(LCEC)算法的相控阵雷达系统对干扰抑制和旁瓣压低性能。建立了均匀线阵接收信号模型，给出了LCMV，LCEC两种算法的原理，用仿真方法讨论了不同数据率和阵元数时LCMV，LCEC算法不同到达方向上的干扰与旁瓣抑制性能。结果表明：与LCMV算法相比，高数据率、低阵元数时LCEC算法在两个相隔角度小于1个主波束宽带的干扰来波方向上形成的零陷更准确；低数据率、低阵元数时LCEC算法的角度分辨率更高；低数据率、高阵元数时LCEC算法的副瓣电平抑制能力更强，高阵元数时LCEC算法保持了静态方向图的特征。

相控阵雷达； 低数据率； 低阵元数； 线性约束最小方差算法； 线性约束特征干扰相消器； 干扰抑制； 天线旁瓣； 自适应波束形成

0 引言

相控阵雷达是提高导弹武器系统作战效能的重要手段。对长时间工作的相控阵雷达系统，要求进行有效的能量管理以解决散热问题，此时相控阵雷达系统需采用间断照射的低数据率工作方式，对小型相控阵雷达系统来说还存在阵元数较少的问题。因此，提高低数据率和低阵元数时相控阵雷达系统的作战效能有重要作用。

敌方重要空中目标周边常存在多架随行干扰飞机，其发射的干扰信号可能从不同的方向通过雷达系统天线波束旁瓣进入接收机，影响雷达系统的正常工作[1]。当敌方机群距离较远时，可能出现雷达系统观测到的多架干扰机间的角度间隔较小的状况，因此对小角度间隔的随行干扰飞机辐射的干扰信号抑制是雷达系统抗干扰中的重要内容。自适应波束形成技术在相控阵雷达系统阵列信号处理中应用广泛。采用自适应波束形成算法对相控阵雷达系统阵元权值进行调整优化，可有效抑制相控阵雷达系统天线波束的旁瓣，并能使相控阵雷达系统天线波束在干扰信号的来波方向自适应形成零陷，有效抑制随行干扰飞机辐射的干扰信号[2]。因此，在低数据率和低阵元数条件下，使相控阵雷达系统对干扰信号进行有效抑制值得研究。文献[3]实现了基于对角载入的波束形成算法，在低数据率下算法具稳健性，且简单有效，但需正确估计对角载入的具体值。文献[4]提出了一种改进的正交投影自适应波束形成算法，在低数据率和低阵元数时的性能较好，但未定量分析在两个干扰来波角度方向非常接近时其角度分辨率性能和零陷角精度。文献[5]提出了一种改进的正交投影自适应波束形成算法，可减小低快拍数下主峰偏移和副瓣电平升高问题，但仍未解决干扰间隔较近时角度分辨率问题，且需要的阵元数较多，副瓣电平起伏较剧烈，没有静态方向图的特征。LCMV，LCEC算法是典型的自适应波束形成算法。LCMV算法于1972年提出，是传统的自适应波束形成算法，通过在最早的Capon自适应波束形成算法中加入线性约束，拓宽了主瓣宽度或在已知的干扰方向上形成零陷，当期望信号来波方向矢量已知时，该算法具较好的角分辨率和干扰抑制能力[6]。LCEC算法基于统计降秩自适应数字波束形成技术，与满秩算法相比，具计算量小，收敛速度快的优点，并在低数据率时有优良的性能[7]。两种算法具成熟、简单和速度快的优点。为使研究在间断照射低数据率和低阵元数条件下工作的相控阵雷达系统抑制多个来波方向干扰的性能更具实际意义，本文研究了LCMV，LCEC两种自适应波束形成算法在低数据率和低阵元数条件下对不同来波方向的干扰信号进行抑制的性能，以及对天线旁瓣的抑制能力。

1 信号模型

考虑有阵元N个的均匀线阵，每个阵元间距为d(d≤λ/2，此处λ为接收信号波长)。均匀线阵的接收信号模型如图1所示。天线阵列接收了来波方向分别为θ1，θ2，…，θK的K个远场窄带不相关信号。假设所有信号的均值为0，天线接收到的噪声为服从均值0、方差σ2的高斯白噪声[8-9]。

图1 均匀线阵接收信号模型Fig.1 Model of uniforms linear array

采用第0个阵元作为参考，天线阵接收到的数据可表示为

X(n)=AS(n)+N(n).

(1)

式中：X(n)，S(n)，N(n)，A(n)分别为接收数据向量、期望信号向量、噪声向量和方向矩阵，且

X(n)=[x0(n)x1(n) …xN-1(n)]Τ，

S(n)=[s0(n)s1(n) …sK(n)]Τ，

N(n)=[n0(n)n1(n) …nK(n)]Τ，

A(n)=[a(θ1)a(θ2) …a(θK)].

此处：a(θK)为导向向量，且

a(θK)=[1e-jφk…e-j(N-1)φk]Τ.

其中：φk=2πdsinθk/λ。

阵列信号的协方差矩阵可表示为

R=E[X(n)(X(n))H]=ARSAH+σ2I.

(2)

式中：RS为期望信号的协方差阵，且RS=E[S(n)×(S(n))H]；I为单位阵。

2 线性约束最小方差算法

LCMV算法是在保证期望信号S的增益为常数条件下，最大化输出信噪比，这在维持期望信号能量恒定时等效于最小化输出信号的总功率[10-11]。基于此原理，可得用LCMV算法求解阵列最优权值向量即为求解线性约束最小方差函数

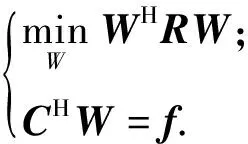
(3)

式中：C为N×K维的信号方向约束矩阵；N为阵元数；K为存在的期望信号数；f为相对应的K×1维的约束响应向量；R为阵列信号的协方差阵。由文献[9]，求解式(3)可得LCMV算法的最优权值向量

WLCMV=R-1C(CHR-1C)-1f.

(4)

3 线性约束特征干扰相消器

线性约束特征干扰相消器(LCEC)采用超分辨谱估计[10-11]。该算法能在噪声子空间中约束阵列的权值向量，从而实现了超角度分辨的干扰对消性能。该算法可在3 dB主波束宽度内形成多个准确的干扰零陷，并解决了多个相隔较近的干扰相互抑制，导致零陷位置偏离真实的干扰角度，甚至无法对每个干扰都产生零陷的问题。

LCEC算法的原理是对接收信号的协方差矩阵进行特征分解，从而得到干扰子空间，这样能间接地提取处干扰信号，再通过干扰特征向量约束抑制干扰，相当于在干扰方向施加零点约束。

假设阵列的接收信号中仅含干扰、杂波和噪声，接收信号向量可表示为

X(n)=[x0(n) x1(n) … xN-1(n)]T，

接收信号的协方差矩阵为Rxx。对Rxx进行特征分解，可得特征值N个，也能得到特征值对应的特征向量，其表达式为

USΛS(US)H+UnΛn(Un)H.

(5)

式中：λi为特征值(i=0，1，2，…，N-1)；ui为λi对应的特征向量；US，Un分别为干扰子空间和噪声子空间；ΛS，Λn为相应空间的对角阵，对角阵元素为US，Un中各特征值向量对应的特征值。将特征值由大到小排列，排在前面数个绝对值较大特征值λi(i=0，1，2，…，K-1)对应的是干扰信号的特征值，其对应的特征向量构成了US，剩余绝对值较小的特征值λi(i=K，K+1，…，N-1)对应的是噪声信号的特征值，其对应的特征向量构成了Un。

由此可得用LCEC算法求解阵列最优权值向量的优化函数

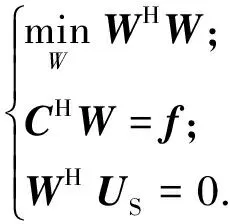
(6)

由文献[9]，用拉格朗日求解法求解式(6)，可得LCEC算法的最优权值向量

WLCEC=Un(Un)HC[CHUn(Un)HC]-1f.

(7)

4 仿真与分析

对高数据率和低数据率时LCMV，LCEC算法的干扰抑制和旁瓣抑制性能进行仿真分析，设阵列天线为均匀线阵，改变数据速率(快拍数)和阵元数，用蒙特卡罗方法试验，仿真200次后求平均。

4.1 高数据率时算法性能

取均匀线阵的阵元数分别为8，32个，阵元间距为λ/2，期望信号方向0°。两个不相关的干扰来波角度分别为10°，13°，两个干扰来波角度间隔很近，小于一个主波束宽度,干噪比分别为10,20 dB。采用快拍数为640的高数据率。噪声为加性高斯白噪声。对LCMV，LCEC算法的性能进行仿真，结果分别如图2、3所示。

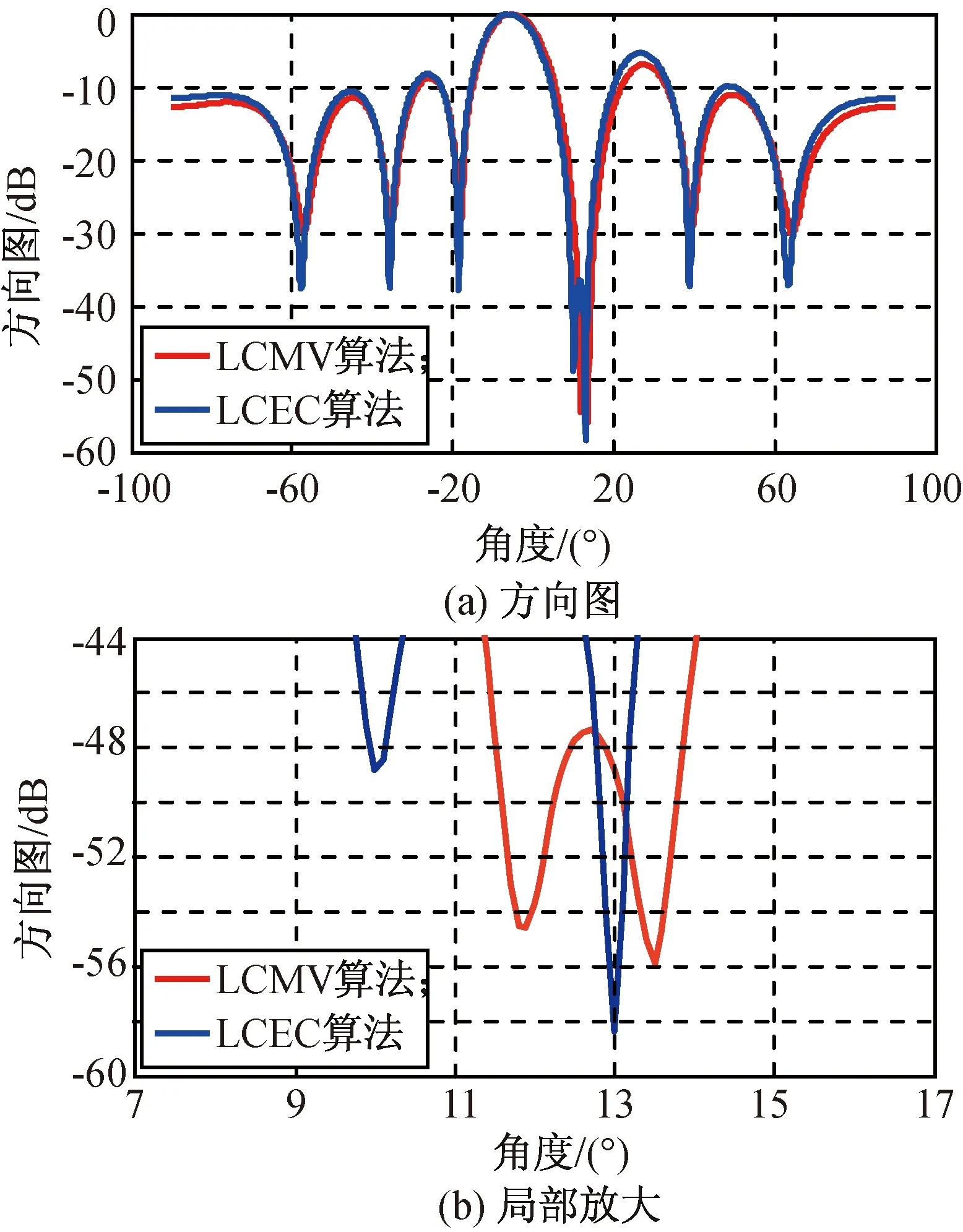
图2 阵元数8时高数据率下两种波束形成算法性能Fig.2 Beamformers’ beam patterns with 8 elements in high data rate

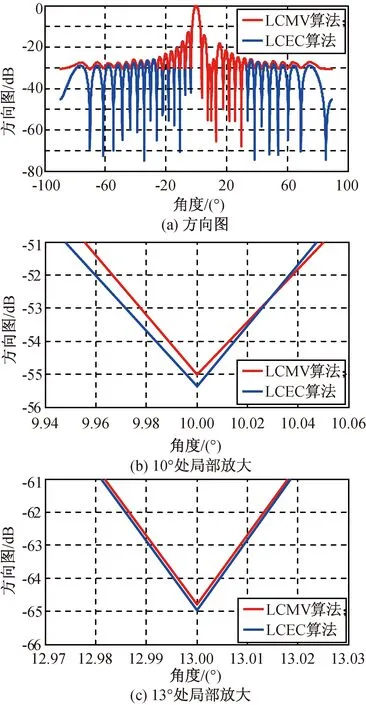
图3 阵元数32时高数据率下两种波束形成算法性能Fig.3 Beamformers’ beam patterns with 32 elements in high data rate

仿真结果表明：在高数据率、阵元数较多条件下，LCMV，LCEC算法均能在干扰来波方向形成准确的零陷，且两种算法对阵列天线的旁瓣抑制能力基本相同；阵元数减少后(如图2(b))，LCMV算法已不能在两角度间隔小于1个主波束宽度的干扰来波角度上形成准确的零陷，而LCEC算法仍能在两个干扰来波方向上形成准确零陷，且在阵元数较多情况下，LCEC算法还保持了静态方向图副瓣的特征。

4.2 低数据率时算法性能

取均匀线阵的阵元数分别为8，32个，阵元间距为λ/2，期望信号的方向为0°。两个不相关的干扰来波角度分别为10°，13°，干噪比相应为10，20 dB。采用快拍数为64的低数据率，噪声为加性高斯白噪声，对LCMV，LCEC算法性能进行仿真，结果分别如图4、5所示。

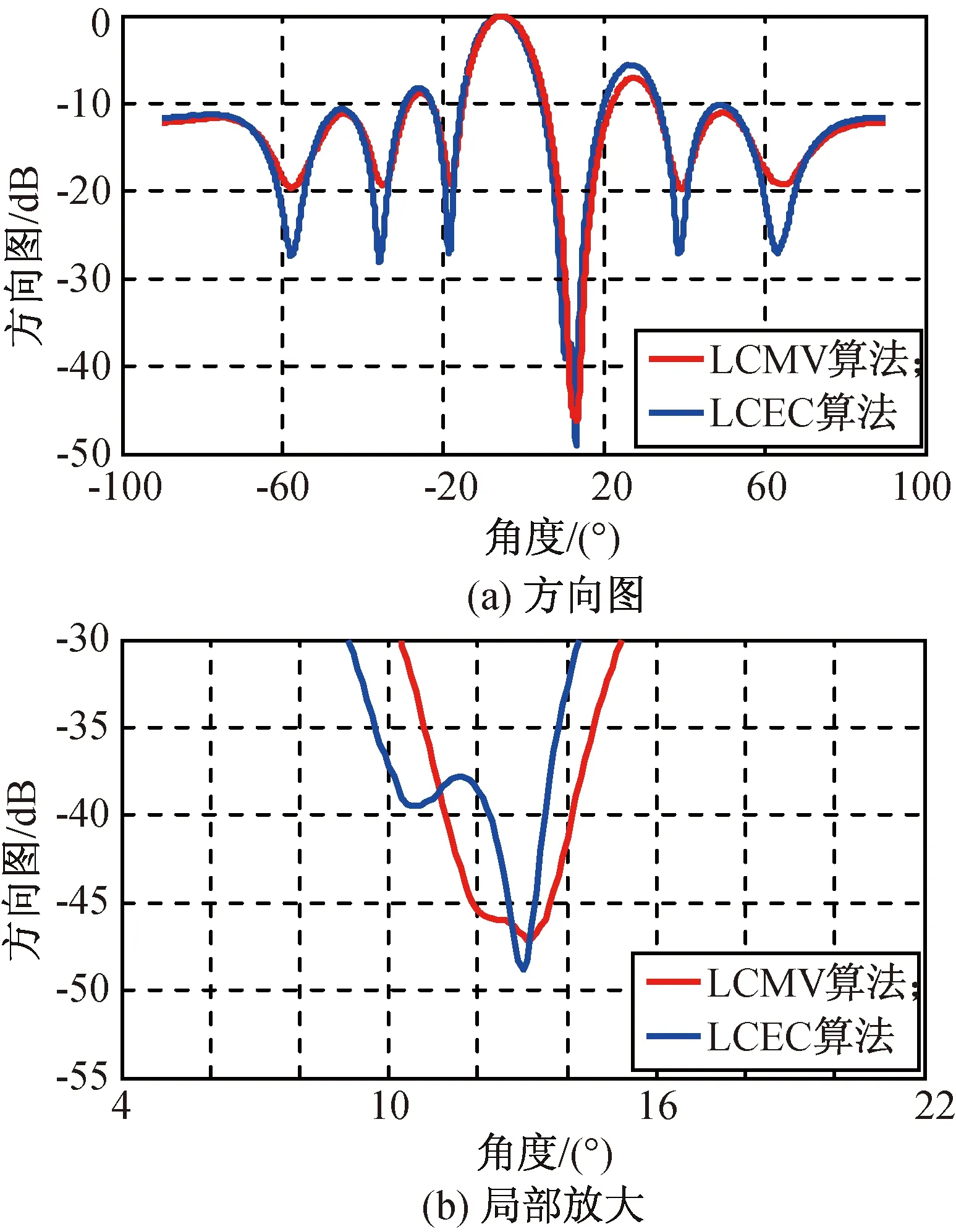
图4 阵元数8时低数据率下两种波束形成算法性能Fig.4 Beamformers’ beam patterns with 8 elements in low data rate

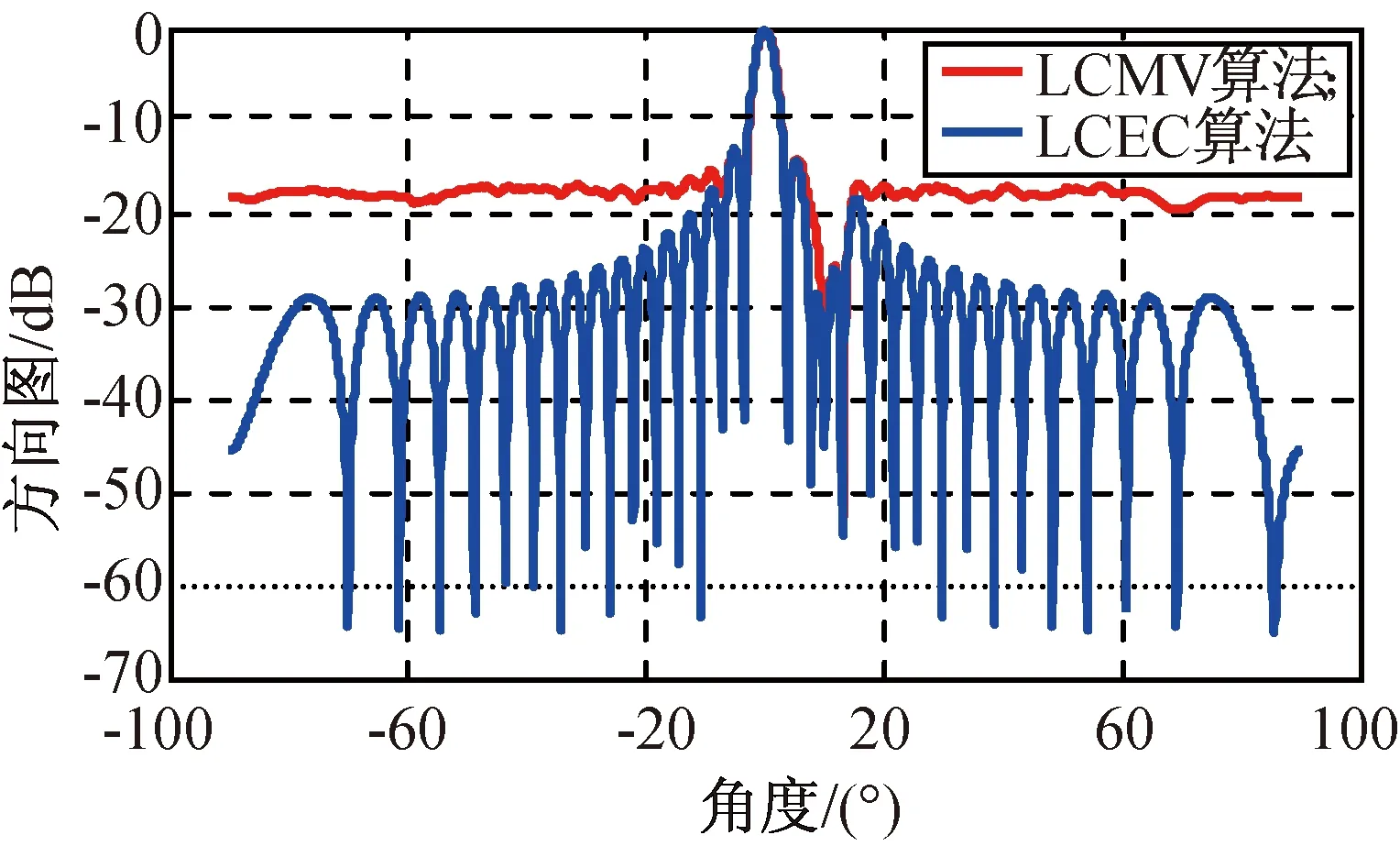
图5 阵元数32时低数据率下两种波束形成算法性能Fig.5 Beamformers’ beam patterns with 32 elements in low data rate

仿真结果表明：当两个干扰方向角度间隔小于1个3 dB主瓣宽度时，在数据率较低、阵元数较少条件下，LCEC算法能分辨出两个干扰零陷位置，但LCMV算法已不能对每个干扰都形成零陷；当阵元数较多时，用LCEC算法进行权值优化的阵列天线能获得更低的副瓣电平，平均可达-30 dB，而用LCEC算法进行权值优化的阵列天线的副瓣电平仅能达到约-20 dB。因此，在低数据率时增加阵元数，能显著提高LCEC算法对副瓣电平的抑制性能，使其远优于LCMV算法，且有更深的零陷，零陷深度最低可至-55 dB，性能优于LCMV算法，同时在阵元数较多时LCEC算法保持了静态方向图副瓣的特征。

不同信息率时LCEC，LCMV算法的性能见表1。由表可知：在不同低数据率和低阵元数条件下，LCEC算法较LCMV算法有更低的旁瓣电平、更高的角度分辨率，在干扰来波方向上能形成更准确的干扰零陷的优越性能。因此，在低信息率条件下LCEC算法的性能优于LCMV算法。与文献[5]EXP-LCMV算法比较发现，在低数据率高阵元数条件下，本文LCEC算法的副瓣电平起伏平缓，具静态方向图特征。与文献[4-5]相比，本文增加了对干扰来波的角度间隔较近时的角度分辨率研究，此研究对解决实际中干扰机角度间隔较小的问题有现实意义。

表1 不同信息率条件下LCEC与LCMV算法性能

5 结束语

本文对LCMV，LCEC两种算法在低数据率和低阵元数条件下干扰与旁瓣抑制的性能进行了研究。结果表明：在高数据率、低阵元数条件下，LCEC算法较LCMV算法能在两个相隔角度小于1个主波束宽带的干扰来波方向上形成更准确的零陷；在低数据率、低阵元数条件下，LCEC算法较LCMV算法有更高的角度分辨率；在低数据率、高阵元数条件下，LCEC算法较LCMV算法有更强的副瓣电平抑制能力。同时，在高阵元数条件下，LCEC算法还保持了静态方向图的特征。因此，LCEC算法可有效提高低信息条件下相控阵雷达系统对副瓣电平的抑制能力、降低干扰零陷和提高角度分辨率，且能提高相控阵雷达系统在高数据率、低阵元数条件下对干扰来波方向的角分辨率。在低信息率条件下，LCEC算法具较LCMV算法更优的性能。本文目前研究仅限于数字仿真，仿真结果尚未得到实际系统的外场测试或半实物仿真试验验证。后续将利用实际系统测试或半实物仿真试验数据对数字仿真结果进行验证，并对其他新型的自适应波束形成算法在低数据率与低阵元数时的性能进行研究分析。

[1] 彭望泽. 防空导弹武器系统电子对抗技术[M]. 北京: 中国宇航出版社, 2009.

[2] 刘翔. 自适应数字波束形成技术研究[D]. 西安: 西安电子科技大学, 2012.

[3] CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic systems, 1988, 24(4): 397-401.

[4] 余继周. 一种改进的正交投影自适应波束形成算法[J]. 上海航天, 2005, 22(4): 6-8.

[5] 李洪涛, 贺亚鹏, 朱晓华, 等. 一种低快拍情况下稳健的波束形成算法[J]. 信号处理, 2011, 27(6): 808-812.

[6] FROST O L. An algorithm for linearly constrained adaptive array processing[J] Proc IEEE, 1972, 60(8): 926-935.

[7] HAIMOVICH A. The eigencanceler: adaptive radar by eigenanalysis methods[J]. IEEE Transactions on Aerospace Electronic Systems, 1996, 32(2): 532-542.

[8] 李洪涛, 贺亚鹏, 朱晓华, 等. 冲击噪声背景下基于归一化的线性约束特征干扰相消器[J]. 信号处理, 2011, 27(5): 795-798.

[9] HUANG Y J, WANG Y W, MENG F J, et al. A spatial spectrum estimation algorithm based on adaptive beamforming nulling[C]// 2013 Fourth International Conference on Intelligent Control and Information Processing (ICICIP). Beijing: [s. n.], 2013: 220-224.

[10] HAIMOVICH A. The eigencanceler: adaptive radar by eigenanalysis methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(2): 532-542.

[11] 丁前军, 王永良, 张永顺. 基于变换的线性约束降秩自适应波束形成算法[J]. 系统工程与电子技术, 2005, 27(12): 2010-2013.

Research on LCMV and LCEC Beamforming Algorithm in Low Data Rate and Low Element Number

LU Jia1, LI Bei-bei2, YANG Ge-wen1, CHEN Zhao-yan1

(1. Shanghai Electromechanical Engineering Institute, Shanghai 201109, China; 2. School of Electronic Engineering and Optoelectronic Technology, Nanjing University of Science & Technology, Nanjing 210094, Jiangsu, China)

The interference rejection and antenna sidelobe restraint of the phased array radar in low data rate and few elements using linearly constrained minimum variance (LCMV) algorithm and linearly constrained eigencanceler (LCEC) algorithm were studied in this paper. The received signal model of homogeneous linear array was established. The LCMV and LCEC algorithms were given out. The restraint performances of interference and antenna sidelobe in various direction of arrival with different data rate and element number for the two algorithms were discussed by simulation. The results showed that the LCEC algorithm had better nulling in the direction with the apart angle smaller than one main beam width under high data rate and low element number, higher angular resolution under low data rate and low element number, and lower antenna sidelobe, which compared with LVMV algorithm. Meanwhile, LCEC algorithm would keep static directional diagram in high element number.

Phased array radar; Low data rate; Low element number; Linearly constrained minimum variance(LCMV) algorithm; Linearly constrained eigencanceler(LCEC); Interference rejection; Antenna sidelobe; Adaptive beamforming

1006-1630(2016)04-0070-05

2016-04-02；

2016-05-22

总装备部预研精导项目资助

陆 加(1991—)，男，硕士，主要研究方向为飞行器无线电制导总体技术。

TN958.92

A

10.19328/j.cnki.1006-1630.2016.04.012