基于星载高速调制器的射频功放线性化技术研究
向 前,李惠媛,杨津浦
(上海航天电子技术研究所,上海201109)
基于星载高速调制器的射频功放线性化技术研究
向 前,李惠媛,杨津浦
(上海航天电子技术研究所,上海201109)
为补偿射频功放非线性失真对高速宽带数传系统的影响,对全数字基带预失真算法进行了研究和改进。用Matlab仿真工具对预失真的最小均方(LMS)、递归最小二乘(RLS)算法进行了分析和比较,提出了一种新的变步长迭代收敛算法。在接收端对调制的中频信号直接采样,无需采集发端数据,用宽带锁相环和相关峰技术实现收、发信息同步,对整个信道的线性和非线性失真进行补偿处理。仿真表明该算法可提高预失真的性能和收敛速度。在星载高速调制器和行波管功放系统中对改进算法后的预失真技术进行了测试,16QAM宽带信号验证结果表明该方案可提高系统性能,减小功放非线性对系统的影响。
星载高速数据传输; 宽带数字预失真; 非线性失真; 调制器; 线性化; 变步长迭代收敛
0 引言
随着遥感卫星及其有效载荷技术的发展,航天器产品获取的信息量和数据量出现了突飞猛进的增长,对提高星地传输速率的需求尤为迫切。为满足未来星地高速数据传输要求,扩大对地观测卫星的应用领域,解决宽带信号频率资源紧张问题,研究高频带利用率的高阶调制数传技术有重要意义[1]。高阶调制的高速数传系统中,采用的16QAM,32APSK等高阶调制方式具非恒定包络调制的特性,星载行波管功放(TWTA)或固态功放(SSPA)的线性化技术是卫星高速数传研究的关键技术瓶颈[2]。信道的非线性对高阶调制信号产生频谱扩展、星座图扭曲和非线性码间干扰等不利影响,严重降低了高速数据传输系统的性能[3]。为消除信道中非线性器件(功率放大器、行波管放大器等)对信号造成的非线性失真,需针对通道设计预失真补偿算法,根据非线性器件实测指标的特点,设计高速、宽带和低复杂度的预失真算法,完成数字预失真功能仿真与硬件实现,并最终完成性能的优化,以及在高速数据传输系统中的应用[4]。
在高速数传射频通道补偿中,采用自适应均衡方法消除信道的线性失真,可减少对非线性预失真方案的影响,并在此前提下对通道内非线性失真进行补偿。传统的数字预失真算法在求解相关参数时,采用收、发同源的闭环链路实现载波同步,但在星载航天器高速宽带的数传系统中,由于星载宽带高速接收解调设备较复杂,高速解调不适于航天器使用,只能在地面实现,很难实现收、发同源。如前馈法方案有较宽的补偿工作带宽,但需额外的辅助补偿放大器,且要求此辅助放大器自身的预失真特性应与被补偿放大器互补,技术难度较大,实现效率较低;安捷伦公司的数字预失真(DPD)硬件测试系统,发端的信号发生器必须单独送一路10 MHz参考时钟至收端的信号分析设备,以保持收、发载波同步,但星载数传设备不可能单独向地面提供一路载波时钟信号。本文对星载高速宽带数据传输系统提出一种宽带数字预失真方案,在接收端对调制后的中频信号直接采样,无需采集发端数据,采用宽带锁相环和相关峰技术实现收、发信息同步,对整个信道的线性和非线性失真做补偿处理,求出其通道失真的补偿系数,利用Matlab的Simulink平台和高速硬件FPGA资源实现高速数据传输系统的预失真技术。
1 链路补偿方案设计
高速数据传输系统的射频通道如图1所示。根据射频通道的器件特性划分信道的线性失真区和非线性失真区。高速数字预失真算法可补偿由放大器、行波管功放等产生的非线性失真。
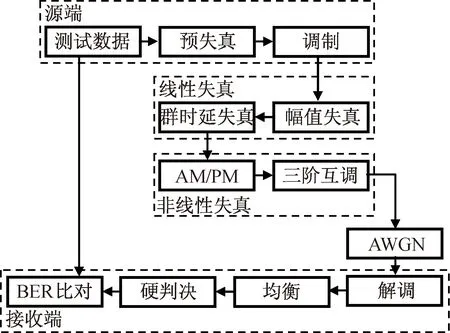
图1 高速数传发射机射频通道Fig.1 RF channel in high-speed data transmitter
源端包括数据生成模块、映射模块、预失真模块和调制模块,可实现测试数据的产生、预失真和调制;信道模拟包括线性失真模块(含幅值和群时延失真)、非线性失真模块(含AM/PM和三阶互调效应)和AWGN模块,可模拟卫星传输信道,添加幅值失真、群时延失真,以及由TWTA造成的AM/PM效应和三阶互调效应,之后添加高斯白噪声;接收端包括解调模块、均衡模块、硬判决模块和BER比对模块,实现数据的接收、解调、均衡、判决及最后的误码率比对[5]。因16QAM较16PSK有4 dB的信噪比增益,综合考虑频带利用率、功率效率和实现复杂度,本文采用16QAM作为高阶数传传输调制方式。
2 预失真算法分析
本文预失真算法用于高速数传通信系统。在宽带应用中,功放的记忆效应变得尤为明显,功放输出不再是输入信号的即时函数,而与过去的输入有关,这严重影响通信系统的正常传输,此时无记忆预失真就不再适用[6]。综合考虑兼顾算法复杂度和宽带信号的算法性能,选用有记忆性的记忆多项式模型作为预失真模型[7]。
2.1 预失真参数求解
经典记忆多项式模型可表示为
(1)
式中:x(n)为输入信号;z(n)为输出信号;K,Q分别为非线性的阶数和记忆深度;akq为模型系数[8]。令Z为预失真器输出矢量,A为预失真系数矢量,U为预失真器输入矢量,则式(1)可表示为
Z=UA.
(2)
式中:
U=[XnXn+1…Xn+l-1]T;
(3)
Z=
[z(n)z(n+1) …z(n+l-1)]T.
(4)
此处:
Xn=
[X1…Xq…Xq(k-1)-1…Xqk].
(5)
其中:X1=x(n)|x(n)|0;X2=x(n-1)|x(n-1)|0;Xq=x(n-q)|x(n-q)|0;Xq(k-1)=x(n)|x(n)|k-1;Xq=x(n-q)|x(n-q)|k-1。
用LMS和RLS算法识别预失真系数。
2.1.1 基于LMS迭代的预失真算法
以n=0,1,2,…,L-1为一组的输入序列,若预失真模型经测试和验证在多项式阶数为k、记忆深度为q时性能最佳,则预失真系数的个数m=kq[9-10]。LMS步骤如下:
a)初始化wm(0)=0;
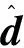
d)系数矢量更新wm(n+1)=wm(n)+μU′lm(n)e(n)。
式中:μ为步长因子,用于控制稳定性和收敛速度,一般0<μ<2/λmax;wm为m维预失真系数向量;U为经功放记忆效应后的输入信号矩阵;e(n)为第n个输入数据的误差值。此处:λmax为输入序列自相关矩阵的最大特征值。
2.1.2 基于RLS迭代的预失真算法
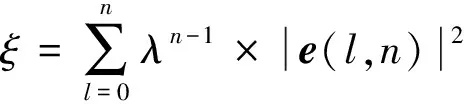
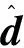
d)计算卡尔曼增益矢量
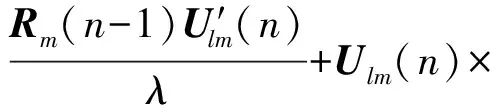
e)更新相关矩阵的逆
Rm(n)=(Rm(n-1)-Kml(n)Ulm(n)×Rm(n-1))/λ;
在整个医学检验质量控制工作中,医学检验人员发挥着至关重要的作用,其是实现医学检验高质量、高效率的基础。但是就目前来看,很多医疗机构内的检验人员在进行医学检验的时候,很容易会出现疏忽大意的情况,没有对医学检验质量进行严格的控制,从而导致医学检验质量大幅下降,使检验结果的准确性得不到有效的保障。
f)系数矢量更新
wm(n+1)=wm(n)+Kml(n)el(n).
式中:δ为很小的正数;Rm为信号(估计)相关矩阵的逆;Im为对Rm初始化的单位阵。
由此可知:LMS中系数矢量的更新为wm(n+1)=wm(n)+μU′lm(n)e(n),μ是唯一可变参数;RLS中系数增益变量是误差乘以增益向量Km(n),而Km(n)为M维,因此每个系数都被增益向量的1个元素调整,算法的收敛更快。
2.2 预失真算法改进
对LMS而言,当步长较大时,权系数会加快收敛速度向最佳系数靠拢,而步长较小时,权系数会以较慢的速度向权系数平稳靠拢,步长选取直接影响LMS的性能。对LMS算法进行仿真研究了步长的影响,发现即使在通过迭代收敛后,不同组的预失真系数对系统的影响仍有较大差距,这说明求最佳预失真系数的算法还不够稳定。本文提出一种简单的算法修正算法中的步长因子,变步长μ(n)的更新可表示为
w(n+1)=w(n)+μ(n)e(n)U(n).
(6)
式中:U(n)为输入预失真器的信号矩阵;μ(n)e(n)·U(n)=Δw(n)为滤波权系数矢量迭代更新的调整量。为实现快速收敛,须合适选择μ(n)的值,常用的方法有多种,多是将步长构造为随迭代次数而变的函数,再进行仿真分析。但类似的构造方法不易获得预失真系数的最佳值,因为函数本身的局限性和复杂性导致需求的参数较难选取。本文用简单易实现的分区间设定步长的方法提高收敛性能,具体方法如下。设经原迭代算法验证的最佳步长为μopt(0<μopt<2),迭代总次数为Ntot,则
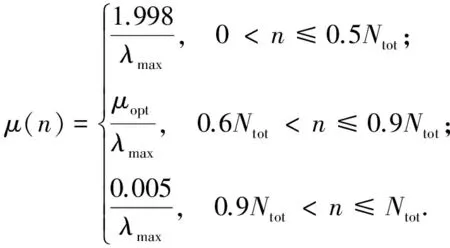
(7)
采用的λmax为经验值,可根据实际需求调整其大小,原则是先用大步长使算法尽快收敛,再用适中步长继续收敛至平稳,最后用较小步长细化增量,实现稳态收敛。该法灵活性大,可根据需要细化分段区间。仿真验证该法在不改动原算法的基础上,通过细化分段区间替换步长可使经预失真后的带外抑制提高约3 dB,这是因为由原算法所得系数并非最佳值,改进算法可更接近最优系数,而预失真对系数选取较敏感,因此提升了预失真的非线性补偿效果。
3 预失真方案仿真实现
3.1 预失真方案的Matlab仿真
本文仿真的发射端用M文件编写了高阶调制的发射序列,接收端采用了Simulink中频仿真程序。将调制后的中频信号直接采样送接收端处理,用宽带锁相环和相关峰技术实现收发信息同步。因高速率数据传输受采样率限制,且实际应用中发送端经功放后均经过带通滤波器进行滤波,故不考虑信号带宽远端的频谱带外抑制,主要分析近端(3倍带宽内)的频谱特性。
LMS算法的数据跟踪结果分别如图2、3所示。由图可知:LMS算法在约400个数据点后开始收敛,收敛后数据跟踪良好。由图2可发现,收敛后的误差波动较大,而预失真系统对模型系数较敏感,需进一步提高算法收敛后的稳定性,使系数随迭代达到最优值。由图3可发现,LMS算法使经过预失真器的实际输出值与理想的期望值间误差较小,说明了算法的正确性。但须在全部迭代中选取一组最佳系数,因此局部的数据吻合并不能使整体的数据效果达到最佳,要求使算法能更稳定地收敛于系数最优解。

图2 LMS算法的误差收敛Fig.2 Error converging performance of LMS algorithm

图3 LMS算法的数据跟踪Fig.3 Data tracking performance of LMS algorithm
RLS算法的数据跟踪结果分别如图4、5所示。由图可知:RLS算法在100个数据点内开始收敛,收敛后数据跟踪良好。仿真结果如前文所述,RLS算法中系数更新受m维元素的控制,其收敛较LMS算法更快。除收敛速度较快外,RLS算法的误差收敛结果和实际信号与期望信号间的吻合性与LMS算法接近。
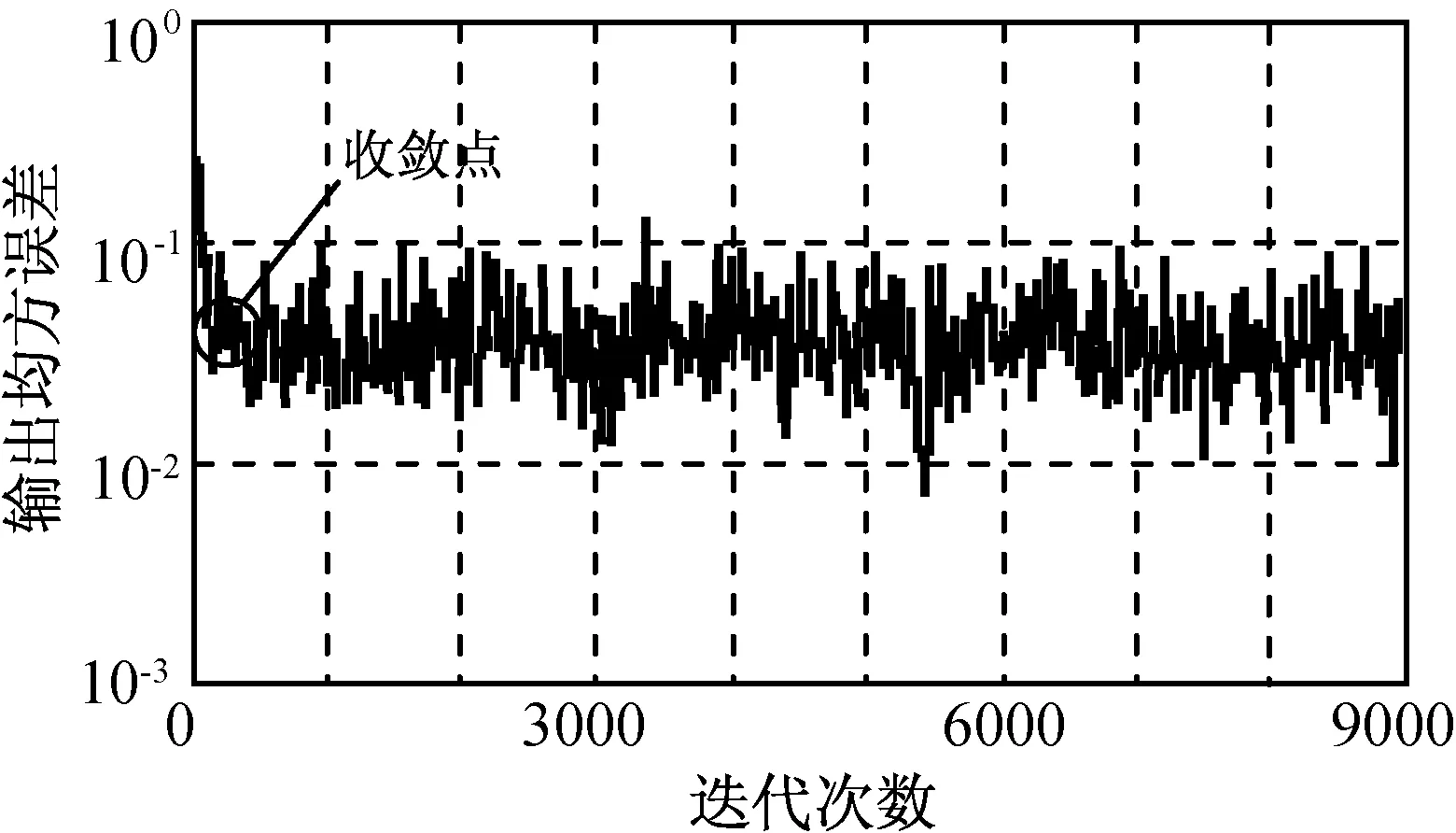
图4 RLS算法的误差收敛Fig.4 Error converging performance of RLS algorithm

图5 RLS算法的数据跟踪Fig.5 Data tracking performance of RLS algorithm
原始信号与经功放的信号,以及用LMS,RLS算法求解的预失真后频谱如图6所示。由图6可知:LMS算法仿真求出的预失真系数可使系统带外抑制提高17.5 dB,而经RLS算法仿真求出的预失真系数可使系统带外抑制提高17.1 dB,两者间并无明显差别。虽然预失真对功放的非线性给予了明显的补偿,但与理想信号相比仍有提高余地。
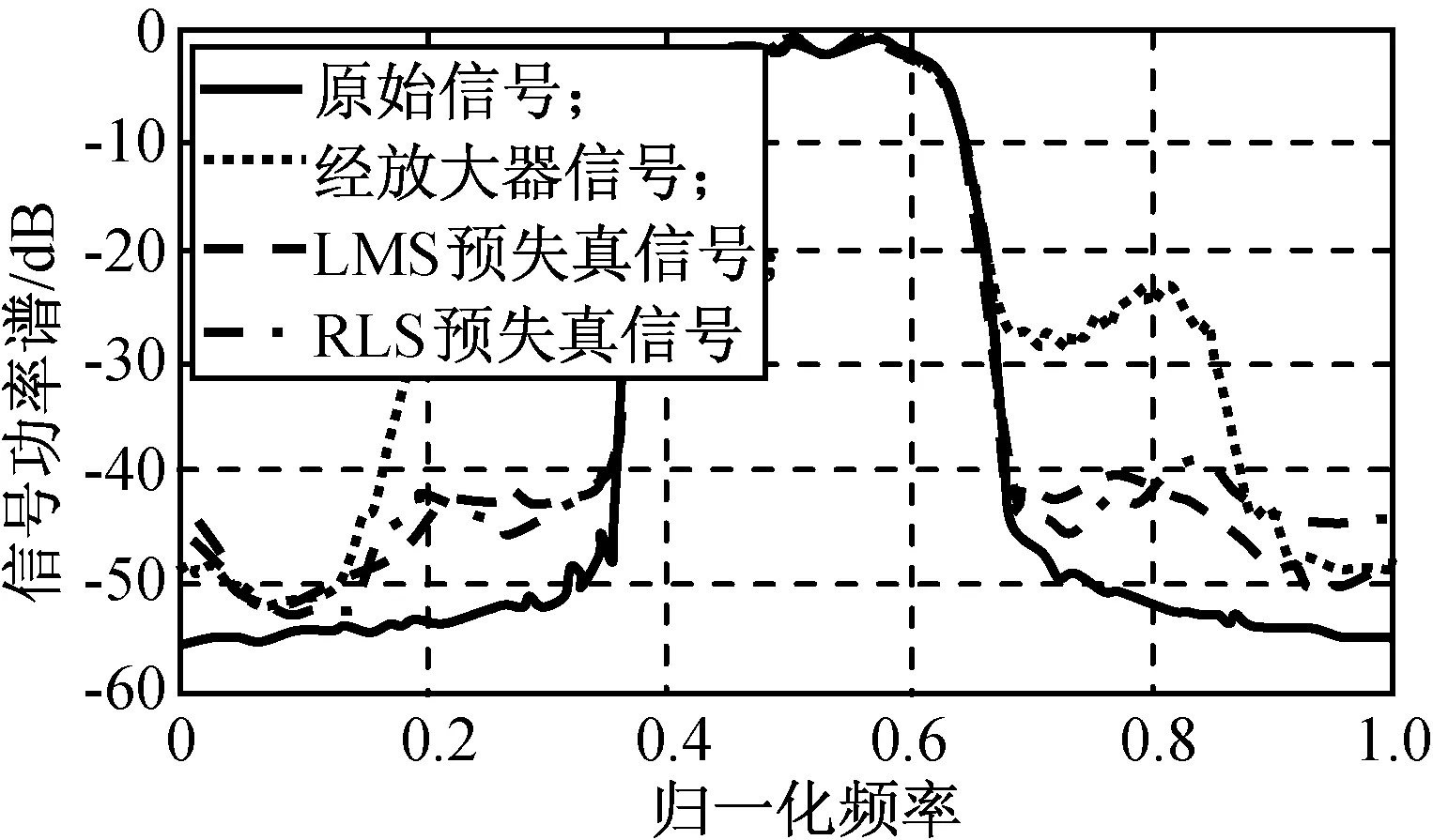
图6 LMS,RLS算法性能Fig.6 Performance analysis of LMS and RLS algorithms
变步长改进后的算法与原LMS算法比较如图7~9所示。由图7、8可知:经预失真所得的实际信号与理想信号几乎完全重合,误差非常小且收敛平稳。由图9可知:改进后算法的带外抑制较LMS算法高3 dB,这是因为改进后的算法在开始时采用了大步长快速收敛于稳定状态,以提高收敛速度,之后采用原算法最佳步长在过渡区间继续收敛并平稳,最后在剩余区间内用较小步长稳定收敛性能,使收敛后误差波动达到最小,更接近于最优解,预失真系统达到更优的补偿状态。

图7 变步长改进算法误差收敛Fig.7 Error converging performance of modified LMS algorithm with variable step

图8 变步长改进算法数据跟踪Fig.8 Data tracking performance of modified LMS algorithm with variable step

图9 变步长改进算法与LMS算法性能Fig.9 Performance of LMS and modified algorithms
3.2 改进算法预失真实测结果
为验证算法在实际应用中可行性,将设计的高速数字预失真算法用于高速数传发射系统。该测试系统主要由星载高速调制器、星载50 W饱和输出行波管功放、下变频器和中频高速解调器组成。
功放的非线性会导致系统性能出现两方面的恶化,一是在带外产生频谱扩散,产生邻信道干扰,二是在带内产生失真,致使系统的EVM和信噪比性能下降,继而使系统误码率性能下降[11]。本文采用16QAM调制方式,平方根升余弦,滚降系数0.5,实测单通道数据传输速率2 Gb/s,调制带宽750 MHz。将行波管功放的输出功率推至接近饱和区的非线性区域,取输入回退功率(IBO)-3 dB,在Ka频段测试,测试结果见表1、2和如图10~13所示。
由图10、12可知:未加数字预失真的调制信号在经过行波管放大器后出现了幅值失真,星座图扭曲(AM/AM,AM/PM效应),同时非线性器件引起的三阶交调失真导致信号的频谱出现了起伏,这样的信号在接收端难以正常解调,系统误码率性能大幅降低。
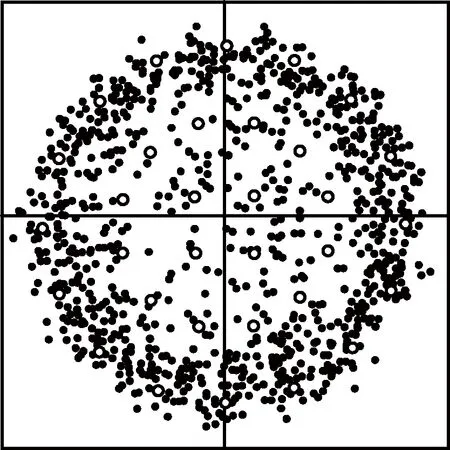
图10 未加预失真星座图测试结果Fig.10 Constellation of system without pre-distortion

图12 未加预失真的频谱测试结果Fig.12 Spectrum performance of system without pre-distortion
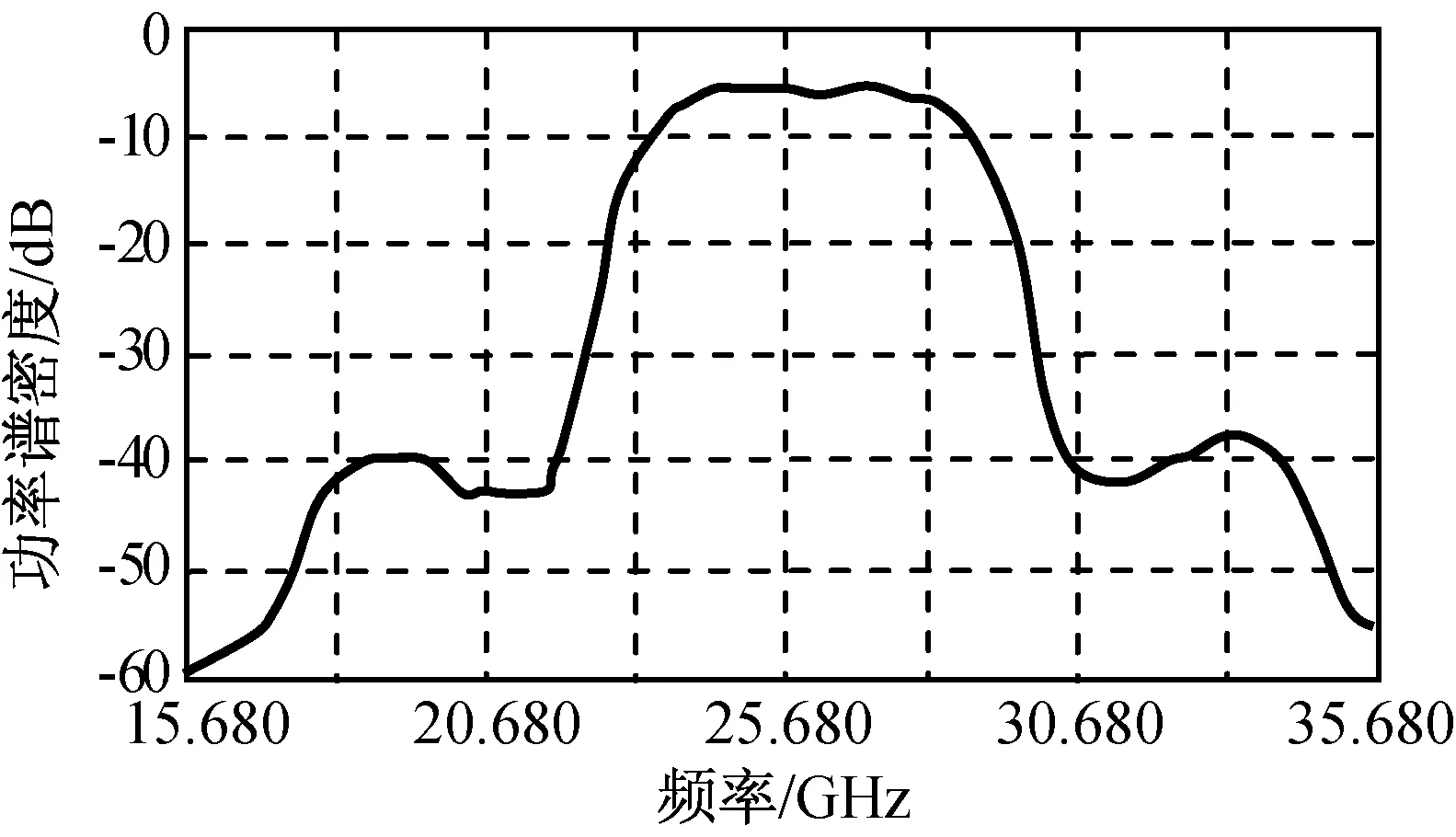
图13 加改进算法后的预失真频谱测试结果Fig.13 Spectrum performance of system with modified pre-distortion
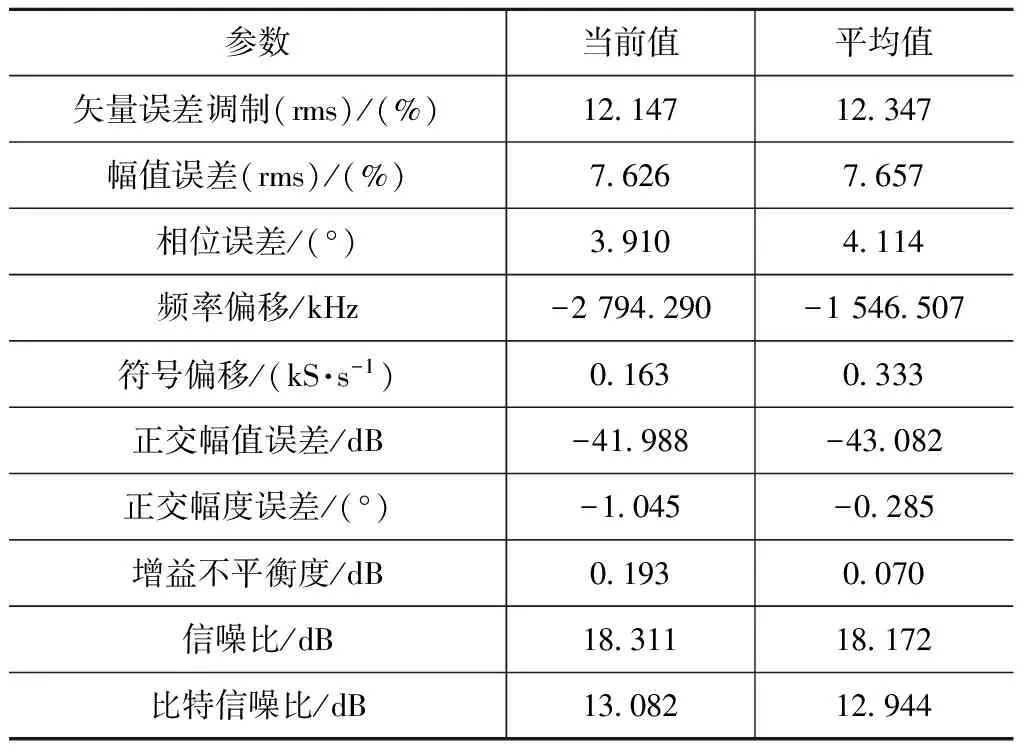
表1 未加预失真系统性能
由图11、13可知:加本文的改进型预失真算法后,星座图获得了明显改善,且三阶带宽内的频谱起伏被较好地控制。
由表1、2可知:数据传输速率2 Gb/s的宽带16QAM信号解调的矢量误差调制(EVM)提高了5.87%(由12.15%提高至6.28%),信噪比提升5.72 dB(由18.31 dB提高至24.03 dB);带外频谱在未加预失真前,3阶交调造成的带外抑制为18 dB,加预失真程序后带外抑制为30 dB,提高13 dB。

表2 加改进算法后预失真系统性能
综上,应用本文改进型预失真算法,调制信号带宽内的信号幅值、相位失真得到了校正,EVM和信噪比指标大幅提高,同时带宽外的频谱抑制也得到了明显改善,整体提升了数传系统的性能。
4 结束语
本文对星载行波管等功放器件的高速、高带宽的数字基带预失真技术进行了研究。提出了一种合理可行的星载数传应用链路补偿方案,可方便灵活地进行星载数传的预失真测试和参数提取;采用并改进了收敛迭代算法,加快了收敛速度,并降低了收敛后的误差波动,提升了预失真补偿性能;搭建了预失真测试系统平台,并对单通道数据传输速率最高达2 Gb/s的16QAM宽带调制信号的非线性补偿效果进行实测,验证了算法的性能,获得了较好的非线性补偿纠正效果。本文研究提出的改进预失真方案有效解决了卫星高速数据传输系统中的射频通道非线性失真问题,提升了数传系统的整体性能,可普遍用于功放的非线性失真补偿,非线性模型和补偿算法与功放具体特性无关。研究为未来星载高阶调制方式奠定了基础。后续,还需研究发送端功能更强大的联合预失真算法,设想可建立数学模型,通过设置少量参数就能生成一个全新的记忆性联合预失真特性曲线,通过产生的特性曲线形成滤波系数查找表进行并行高速流水线相加运算,这样就可用少量的遥控参数产生任意的联合预失真效果,避免了原先查找表系数固定,联合预失真系数不能改变的问题,以此形成星上数传长寿命产品强大的预失真补偿功能,提高失真补偿的智能性和对射频通道及传输信道的自适应性。
[1] 魏致坤, 强龙凯, 刘波, 等. 高速OQPSK调制技术的滤波器选择[J].上海航天, 2014, 31(4): 54-58.
[2] 胡俊杰. 卫星数据传输高速调制器关键技术研究[D]. 北京: 中国科学院空间科学与应用研究中心, 2011.
[3] 侣秀杰. 记忆功率放大器数字预失真技术研究[D]. 大连: 大连理工大学, 2012.
[4] 董明洋. 宽带高速数字预失真实现技术研究[D]. 北京: 北京邮电大学, 2012.
[5] ALADR’ EN L, GARCIA P, LUIS CARRO P. Digital predistortion based on zernike polynomial functions for rf nonlinear power amplifiers[J]. ISWCS, 2012: 865-869.
[6] WOO Y Y, KIM J, YI J, et al. Adaptive digital feedback predistortion technique for linearizing power amplifiers, microwave theory and techniques[J]. IEEE Transactions, 2007, 55(5): 932-940.
[7] ALADR’ E N L, GARCIA P, CARRO P L. Digital predistortion based on Zernike polynomial functions for RF nonlinear power amplifiers[J]. ISWCS, 2012: 865-869.
[8] 郑斌. WCDMA直放站系统中数字预失真技术的设计与实现[D]. 北京: 北京邮电大学, 2010.
[9] PROAKIS J G, MANOLAKIS D G. Digital signal processing principles, algorithms, and applications[M]. 4thEdition. 北京: 电子工业出版社, 2012: 665-682.
[10] PROAKIS J G. Digital communications[M]. 4thEdition. 北京: 电子工业出版社, 2007: 477-507.
[11] 胡欣, 王刚, 王自成. 查找表联合记忆效应补偿技术的宽带自适应预失真算法[J]. 电子与信息学报, 2012, 34(3): 733-738.
Predistortion Linearizer for RF Power Amplifiers in Spaceborne High-Speed Modulator
XIANG Qian, LI Hui-yuan, YANG Jin-pu
(Shanghai Aerospace Electronic Technology Institute, Shanghai 201109, China)
In order to make up the influence of RF nonlinear power amplifiers in high-speed data transmission system, the digital baseband pre-distortion algorithm was studied and improved in this paper. The LMS and RLS algorithms were analyzed by Matlab simulation. A new method of variable step in iterative convergence algorithm was proposed. The modulated intermediate frequency signal was sampled directly at receving end. The wideband phase-locked loop and relative peak were applied to realize the information synchronism of receiving and transmitting without transmitting data sampling. The linear and nonlinear distortions in the whole channel were compensted. The simulation showed that it would improve the performance and convergence speed. The test results of the 16QAM wide-band signal in a spaceborne high-speed modulator and TWTA system showed that the performance of system with the modified predistortion would be improved, and the influence of RF power amplifiers in high-speed data transmission system was reduced.
Spaceborne high-speed data transmission; Wide-band digital pre-distortion; Nonlinear distortion; Modulator; Linearizer; Variable step in iterative covergence
1006-1630(2016)04-0088-07
2015-09-02;
2015-10-17
总装备部高分辨率对地观测系统重大专项(GFZX04013204)
向 前(1980—),男,高级工程师,主要研究方向为高速调制与解调。
TN914
A
10.19328/j.cnki.1006-1630.2016.04.015

