学好几何从明晰几何概念开始
——记“平面图形的认识(一)”中部分概念
范船良
学好几何从明晰几何概念开始
——记“平面图形的认识(一)”中部分概念
范船良

几何是数学中的一个分支,它将引领我们正确地识别图形,进一步了解和掌握图形的更多性质,更重要的是它将提升我们的空间想象能力和严密的逻辑推理能力,这是我们的数学素养中不可或缺的一面.几何概念是指人们思维中对几何图形的认知(它包括定义、公式、结论等).有些同学对几何问题判断不准,思维混乱,推断说理无根无据,其根本原因是因为没有学好几何的基本概念.因此要学好几何,一开始就要十分重视概念的学习.接下来,就以“平面图形的认识(一)”中部分概念为例谈谈如何明晰几何概念,以起到示范的作用.
一、学习几何概念首先要能正确地叙述相关的定义,此时要善于抠字眼、抓主干
1.要抠字眼,抓关键词.例如,互补角、邻补角的关键词是“补”,补成一个平角(只要补成180°即可),而其中的“邻”则又有了对位置上的要求.又如平角的关键词是“角”,角是有顶点的.
再如平行的关键词是“平”,平是指两条直线在同一个平面内.
例1下列说法中,正确的是().
A.互补的两个角若相等,则这两个角都是直角
B.直线是平角
C.不相交的两条直线互相平行
D.和为180°的两个角是邻补角
【正解】A.
2.句子的主干部分就是概念的要点,如“点到直线的距离”可以把句子划分为:(①从直线外一点到这条直线的)(②垂线段的)长度叫作(③点到直线的)距离.句子的主干部分就是概念的要点,即“长度叫作距离”.再从长度与距离的定语可明确什么样的(①、②)长度叫作什么样的(③)距离.
例2判断:直线外一点与直线上各点连接的所有线段中,垂线段最短,把这条垂线段叫作这点到这条直线的距离.().
【正解】×.
二、学习几何概念要能用字母和符号表示图形的名称、关系,反映出概念的本质
例如,在碰到角平分线时,写出OC是∠AOB的平分线的式子:∠AOC=∠BOC=而更容易理解和掌握.
例3下列说法中正确的是().
A.在∠ABC一边的延长线上取一点D
B.延长直线a、b交于点C
C.反向延长∠AOB的平分线
D.已知线段AB=10 cm,在AB上取一点C,使AC=7 cm,CB=4 cm
【解析】∠ABC一边本身就是射线,可向一方无限延伸,不需要延长.而D中的画图语句与两线段的和不相符,不可操作.故选C.
另外,还要善于分类比较.把容易混淆的概念集中在一起研究,分清其区别和联系,做到准确地理解概念的实质.例如,在表示线段、射线、直线时,一般应在字母的前面注明“线段”“射线”或“直线”.找线段时可找线段的两个端点,找射线时应找一个端点及延伸方向,而任意两点确定一条直线.
例4图1中共有_______条线段,_______条直线,能用字母表示的射线有_______条.

图1
【解析】同一个图形的符号表达形式可以不同,例如以点A、B为端点的线段可以表示为线段AB,也可以表示为线段BA,表示的是同一条线段,又如射线AB与射线AC算同一条射线,其他类同.正确填法是:3,1,4.
三、学习几何概念一定要能正确地画出反映概念的图形,能画出不同形式、不同位置的图形
例5如图2,已知△ABC,
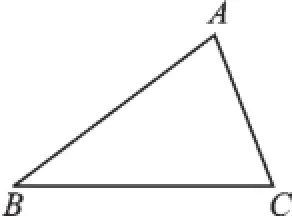
图2
(1)量取线段BC的中点D,并连结AD;
(2)过点A画BC的垂线,垂足为E;
(3)过E画AB的平行线交AC于点F;
(4)画∠ABC的平分线,交AC于G.
【解析】“连结AD”是指画线段AD;“垂线”在几何概念中专指“垂直的直线”,而不是指垂线段或垂直的射线;其中的“角平分线”是专指射线,而不是其他线.这说明对概念的理解不能有任何的偏差.
例6判断:若AC=BC,则点C是线段AB的中点.().
【解析】题中的点C可以在线段AB上,也可以在线段AB外,故此判断为“×”.
例7平面内有两个角∠AOB=50°,∠AOC=20°,OA为两角的公共边,则∠BOC为().
A.30°B.70° C.30°或70°D.无法确定
【解析】根据题意可知要分两种情况,一种是OC在∠AOB内部,另一种是OC在∠AOB外部.画出图形并结合图形计算可得∠BOC等于70°或30°,故选C.
四、学习几何概念要能在复杂的图形中正确地识别表示某个概念的那部分基本图形,也能把几个简单的图形组合成一个较复杂的图形
例8如图3,能表示点到直线(或线段)的距离的线段有().
A.2条B.3条C.4条D.5条
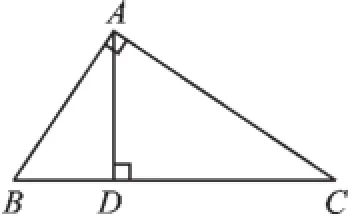
图3
【解析】本题考查的是点到直线的距离的基本图形,例如图中有表示点C到线段AB距离的线段CA和点C到线段AD距离的线段CD,其他也可以这样类似地去找基本图形,本题答案:D.
五、学习几何概念要能运用概念进行简单的判断、推理和计算,要在运用中强化和巩固概念,进而形成概念系统化
例9在例8图中∠C与∠DAB相等的理由是___________________.
【解析】在本章中,要学会用“因为……,所以……”的方式进行简单推理,关键是弄清“因”与“果”的关系,逐步形成思维的逻辑性和条理性.例如,这两个角没有直接的关系,但都与∠B互余,因此填的理由应为:同角的余角相等.
例10如图4,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线.
(1)∠DOE的补角有______________;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由.
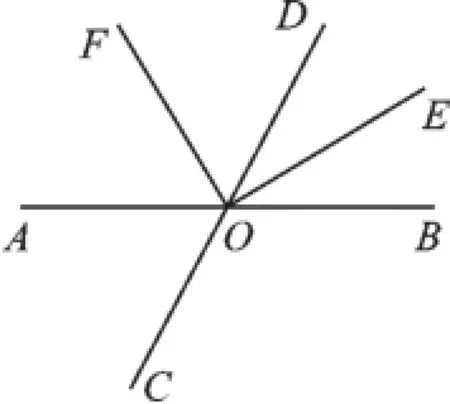
图4
【解析】本题考查余角与补角、角平分线的定义、角度的计算,熟记性质并准确识图,找出图中各角之间的关系是解题的关键.填(1)中的空(求补角而不是求邻补角),必须概念清晰,才能有条理思考问题,而对于(2)、(3)则要掌握用符号来进行有条理的推理的格式.
答案:(1)∠COE,∠AOE;(2)∠AOE= 149°,∠DOF=59°;(3)互相垂直.
一位清华大学学生在学习经验交流中就提及数学的学习是从概念的学习开始的,要更好地了解和掌握概念有一个办法就是适量做一些与概念有关的判断题和选择、填空题,这会从各个不同的角度来辨析它.要学好几何就让我们从正确理解几何概念开始吧.
(作者单位:江苏省吴江区实验初级中学)

