基于强认证理论的三方网络协议安全性证明*

肖美华，刘欣倩,2+，李娅楠，程道雷，梅映天

1.华东交通大学 软件学院，南昌 330013

2.中国人民财产保险股份有限公司宁波市分公司 信息技术部，浙江 宁波 315000

基于强认证理论的三方网络协议安全性证明*

肖美华1，刘欣倩1,2+，李娅楠1，程道雷1，梅映天1

1.华东交通大学 软件学院，南昌 330013

2.中国人民财产保险股份有限公司宁波市分公司 信息技术部，浙江 宁波 315000

XIAO Meihua,LIU Xinqian,LI Yanan,et al.Security certification of three-party network protocols based on strong authentication theory.Journal of Frontiers of Computer Science and Technology,2016,10(12)：1701-1710.

形式化方法是分析网络安全协议的一种重要方法，网络协议安全性也是信息安全领域的研究热点。事件逻辑是一种描述分布式系统中状态迁移的形式化方法，用于证明网络安全协议的安全性。以事件逻辑为基础，定义强匹配及匹配会话，结合事件逻辑公理和推理规则，提出了强认证理论。利用该理论对有3个主体的Neuman-Stubblebine协议进行了研究，分析得出发送者是安全的而接收者是不安全的，从而证明了该协议是不安全的，说明了强认证理论适用于三方的网络安全协议。该理论适用于类似多方网络安全协议的安全性证明。

形式化方法；事件逻辑；强认证理论；Neuman-Stubblebine协议

1 引言

证明网络协议的安全属性是一个复杂的问题。形式化方法是一种强大的证明网络协议的安全属性的方法，其包括模态逻辑、定理证明和模型检测[1]。模态逻辑和定理证明又可笼统地归为一类。模型检测自动化程度高，用来验证系统的不安全性，但是只能对有限数量的并行通信进行研究，难以解决状态爆炸问题。基于定理证明的形式化分析方法是对协议进行建模或对协议需满足的性质进行形式化描述，再用定理证明的技术来证明性质是否在协议模型中被满足。定理证明最大的优点是避免了模型检测中状态爆炸的问题，缺点是证明过程难以完全自动化，并需要有一定的专业知识。许多学者对定理证明方法进行了深入的研究，并取得了非凡的成就[2-5]。

事件逻辑[6-13]是由美国康奈尔大学的Bickford等人于2003年提出的一种定理证明方法，是一种描述分布式系统下协议和算法的逻辑，可以对安全协议一些基本原语进行形式化规约[6]。它采用标准逻辑概念，对安全协议的7种动作，即生成挑战数、发送消息、接收消息、加密、解密、签名和验证，进行形式化描述，同时给出协议中密钥、挑战数和协议消息的形式化描述。本文以事件逻辑为基础，定义强匹配及匹配会话，结合事件逻辑公理和推理规则，提出强认证理论。专注于将网络安全协议用形式化描述后，在符合强认证理论条件下，利用强认证理论，可证明协议的安全性。

本文结构安排如下：第2章简要介绍事件逻辑形式化理论，该部分贯穿全文；第3章形式化定义强认证理论；第4章对Neuman-Stubblebine协议进行详细证明；第5章为结论。

2 事件逻辑

事件逻辑是一种描述并发与分布式系统下协议和算法的逻辑。

2.1 符号说明

该部分描述分析密码协议安全性质的符号和操作符语义。表1给出一些符号及其语义。

2.2 基本概念及定义

（1）Atom

一个atom类（Atom）来表示秘密信息，其中的成员用atoms来表示。

（2）独立性原始命题

(x:T||a)表示类型T中的x不包含原子a。当类型T从上下文中很明显看出时，可用x||a来表示x和a独立。

（3）事件结构

事件语言是任何语言的扩展 E,loc,＜,in fo，这里loc是E上的函数，＜是E上的一个关系，对于e∈E，loc(e)是事件的存储单元，e1＜e2表示事件e1在事件e2之前发生。事件结构中存储单元表示主体、进程或线程。事件结构是满足下边公理的建模：

①≤表示局部有限偏序（每个事件e有有限个前驱）；

② e1＜loce2≡e1＜e2∧loc(e1)=loc(e2)表示局部序，是一个有相同存储单元的事件集的全序；

③in fo(e)和事件e的原始信息相关，通常事件e发生时这个消息转发给loc(e)认证理论中，loc(e)是事件e发生的主体，因此对一些标识符A来说loc(e)=A。

本文将(e′＜e∧loc(e′)=loc(e))缩写为e′＜loce。

Table 1 Basic symbols and semantics of event logic表1 事件逻辑的基本符号和语义

（4）事件类

将身份认证协议中的事件进行分类，其中存在发送、接收、挑战数、签名、验证、加密和解密事件。每类中的事件都有相关信息，且这些信息的类型由事件类决定。定义如下：

2.3 相关公理及规则

事件逻辑包括6种公理，这6种公理分别为密钥公理、因果公理、不相交公理、诚实公理、流关系和随机数公理。下面简要介绍证明过程中需要用到的公理。

（1）因果公理

因果公理包含3个公理，将Rcv类、Verify类和Decrypt类的相关事件公理表示为 AxiomR公理、AxiomV公理和AxiomD公理，与之前相应的Send类、Sign类和Encrypt类中的事件因果对应。AxiomR公理和AxiomV公理相似，也就是说在任何接收或者验证事件之前必须有一个具有相同相关信息的发送或者签名事件。

AxiomD与AxiomR公理类似，解密事件与之前的加密事件拥有相同的相关信息，但是密钥是一个匹配密钥而不是相同密钥。

（2）诚实公理

诚实主体不释放它们的私钥，因此签名事件拥有诚实的签名者；诚实主体私钥的加密事件和解密事件必须发生在该主体，称这个公理为AxiomS。

（3）随机数公理

将随机数公理记为AxiomF，包括三部分。第一部分为：

AxiomF的其他两部分声明了签名、密文和包含它们的事件之间的相似关系。不同的是，没有假设的签名和加密总与特殊事件有关，因此如果一个行为包含签名或者密文，只能推断出具有相同信息的一些签名或者加密动作，流关系如下：

引理3如果e1,e2∈E(New)且New(e1)=New(e2)，则e1=e2。

引理4（随机数释放引理）如果协议Protocol(bss)是合法的，A是诚实主体且遵守Pr，且thr是基本序列bss的一个实例，n=thr[j]，n∈E(New)，e=thr[i]和j＜i，那么如果j和i之间没有一个k是E(Send)中的thr[k]，则随机数New(n)不在e之前释放。

2.4 基本序列

基本序列本质上是协议动作的一个参数列表，其中两个参数是主体的标识符，记为A和B。遵守协议的主体A可以参与到任何多个线程中，其中任何一个线程都是协议基本序列的一个实例，且任何可能不同的主体都扮演着B的角色，并且允许基本序列中超过两个主体。

如果主体A中的每一个动作都是它基本序列中的一个实例成员，则称主体A遵守协议；如果签名和密文动作不正确，那么验证和解密动作在一个序列中不会出现。相似地，如果其他主体失效或者行为不当，那么下一个序列中的接收动作可能不会出现。

一般情况下，一个基本序列是两个主体（也可以是多个主体）和一个线程的关系。当线程是已给主体基本序列中的一个实例，那么关系为真。因此，基本序列是Basic类型的一个成员。

一个基本序列用一个自由变量协议动作列表来定义，所有自由变量，除了A和B都解读为原子。由于基本序列的每一个实例可能生成不同的随机数、签名等，在序列定义的关系中原子参数存在量化。如果loc(thr)=A∧∃B:Id.∃b∈bss.b(A,B,thr)，那么线程thr是主体A中已知bss列表基本序列关系中的一个，记作thr=oneof(bss,A)。

关系inoneof(e,thr,bss,A)用协议的形式化定义为：e∈thr∧thr=oneof(bss,A)。

3 强认证理论

以事件逻辑为基础，定义强匹配及匹配会话，结合事件逻辑公理和推理规则，得出强认证理论。本文分线程、匹配会话和认证三部分说明。

3.1 线程

在单个主体中线程是动作的一个有序列表。

如果第一个发送和第二个接收具有相同的信息，那么s和r这两个消息是一个弱匹配。如果s是r的前因，那么它们构成一个强匹配。

3.2 匹配会话

线程thr1和thr2构成一个长度为n的匹配会话，如果它们都包含至少n个消息，且当每个线程中的前n个消息是成对的，每对满足m1↦m2∨m2↦ m1。这种情况下，定义强匹配会话，记作。如果每一对只满足m1～m2∨m2～m1，得到一个弱匹配会话，记作。

一个协议保证在不同主体上，两个线程之间的一个强匹配会话，称该协议满足一个强身份认证性质，这种理论称为强认证理论。强性质防止重放攻击并且比省略因果序要求的对应的弱认证性质更难证明。

3.3 认证

如果主体A执行一个具有参数B的全部发起者序列中的一个实例，那么倘若B是诚实主体，且也遵守相应的协议，需要主体B的一个应答序列实例与协议中前两个消息构成一个匹配会话（不能保证主体A发送的第三个消息将会被主体B接收到）。类似的，如果主体B执行全应答序列中的一个实例，那么应该有一个和主体A匹配的会话。

强认证理论的形式化定义指出协议中基本序列bs认证n个消息的Pr。

4 Neuman-Stubblebine协议证明

本章运用上文强认证理论分析证明Neuman-Stubblebine协议。

4.1 协议的形式化分析及描述

Neuman-Stubblebine协议[14-15]是一个基于随机数的，以通过服务器来实现通信主体的双向认证以及会话密钥分配为目标的安全协议。认证过程主要分为两个阶段：第一阶段为初始认证阶段，由通过服务器实现发起者和响应者的双向身份认证和会话密钥分配的4条消息组成；第二阶段为继认证阶段，由通过服务器实现发起者与响应者的再次身份认证的3条消息组成。密钥服务器在后继认证阶段不再参与该协议。本文只针对初始认证阶段的安全性进行研究。协议交换过程如图1所示。

（1）A→B：A，RA

（2）B→S：A，B，RB，{A，RA，TB}KB

（3）S→A：{B，RA，K，TB}KA，{A，K，TB}KB，RB

（4）A→B：{A，K，TB}KB，{RB}K

利用事件逻辑对Neuman-Stubblebine协议进行基本序列排序，协议描述如图2所示。

Fig.1 Neuman-Stubblebine protocol图1 Neuman-Stubblebine协议

Neuman-Stubblebine协议的基本序列如下：

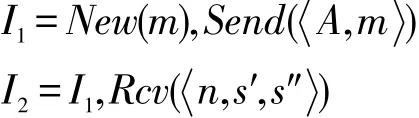
4.2 协议证明过程

利用之前定义的基本序列关系，定义Neuman-Stubblebine协议为Protocol([I1,I2,I3,R1,R2,R3,S1,S2])。要验证的强身份认证性质为：

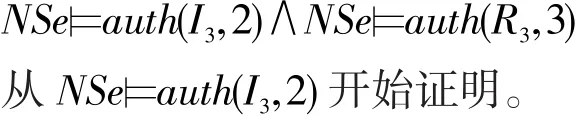
证明 假设诚实主体A≠B≠C且遵守Neuman-Stubblebine协议，并假设线程thr1是I3的一个实例。令e0＜loce1＜loc…＜loce5为thr1上的动作，那么e0,e1,…,e5的主体均为A。对一些atomsm,n,K,TB,s′,s″有：

根据AxiomD和AxiomS，存在一个事件e′使得e′＜e3∧DEMatch(e3,e′)∧loc(e′)=B∨loc(e′)=C成立。那么。

Fig.2 Description of Neuman-Stubblebine protocol图2 Neuman-Stubblebine协议描述

因为B、C都遵守Neuman-Stubblebine协议，动作e′必须为协议的基本序列之中的一个实例成员。唯一一些包含Encrypt(_)动作的是I3、R1、R2、R3、S2，接下来逐个证明。

如果e′是I3中的一个实例，那么对于一些atoms m1,n1,K1,s1′′和主体D，有e0′＜loce′，如此：，但是明显不符要求，因此I3排除。

如果e′是R1中的一个实例，那么对于一些atoms m2,n2,TB2,s2和主体E，在主体B上存在事件 e0′,e1′, e2′,e3′，如此得：

明显不符合要求，排除R1。同理，排除R2和R3。

如果e′是S2中的一个实例，那么对于一些atoms m3,n3,K3,TB3,s3,s3′,s3′和主体F、G，在主体C上存在事件e0′,e1′,e2′,e3′,e4′,e5′，有：

即e3′=e′，因此有F=B,m3=m,k3=k,TB3=TB,s3′=s′，可得：

这样，又必须存在一个事件e″使得e″＜e1′∧DEMatch(e1′,e″)∧loc(e′)=A∨loc(e′)=B成 立。 那 么。因此动作e″必须为协议基本序列中的一个实例成员。唯一一些包含Encrypt(_)动作的是I3、R1、R2、R3、S2，逐个证明。

如果e″是I3上的一个实例，那么对于一些atoms m4,n4,K4,TB4,s4′,s4′,s4′′和主体H，在主体A中有事件e0′,e1′,e2′,e3′,e4′，得：

由此可见明显不符合要求，排除I3。

如果e″是S2上的一个实例，那么对于一些atoms m5,n5,K5,TB5,s5,s5′,s5′和主体J、L，在主体C中有事件e0′,e1′,e2′,e3′,e4′,e5′，得：

可以看到明显不符要求，排除S2。

如果e″是R1上的一个实例，那么对于一些atoms m6,n6,TB6,s6和主体O，在主体B中有事件e0′,e1′,e2′, e3′，得：

即e2′=e″，因此有O=G,m6=m，TB6=TB,s6=s3，可得：

由引理4可知，在随机数m释放之前不会产生一个相同的随机数m，因此在Rcv(e0′)=G,m=A,m中G=A，将之代入式（1）和式（2）中，得：

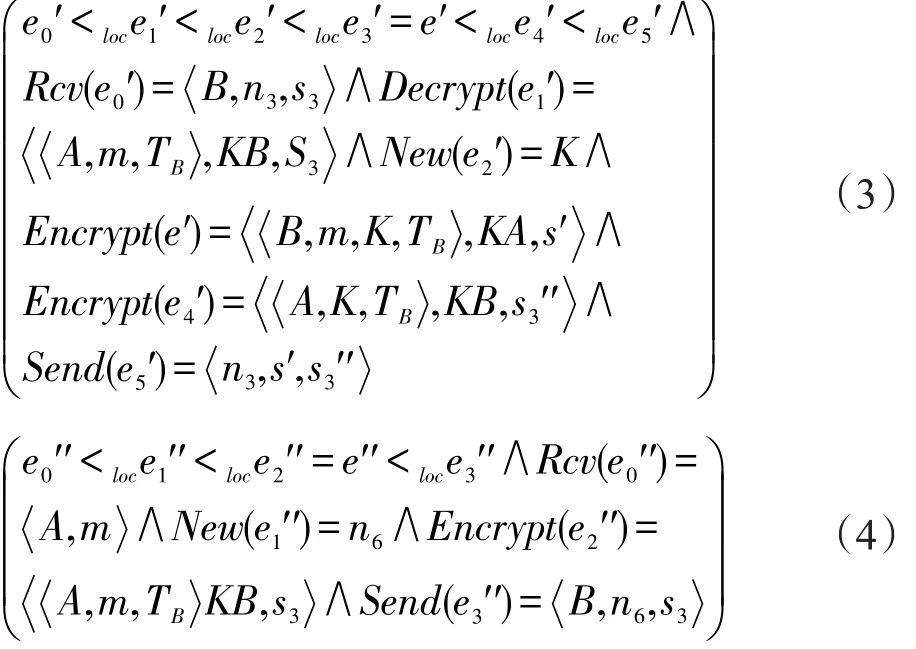
通过引理4可知，在Send(e5′)=n3,s′,s3′中n3= n,s3′=s″，再将之代入式（3）中，得：

因此可以得到Send(e1)=A,m=Rcv(e0′)和Rcv(e2)= n,s′,s″=Send(e5′)。这样就有一个长度为2的（弱）匹配会话。

要想有一个强匹配会话，必须证明e1＜e0′和e5′＜e2。由上文可知通过AxiomF、引理2和假设A≠D，它遵循在e0和e0′之间存在一个发送事件S释放随机数m。如果e1≤j，那么得到的排序为e1＜e0′，再排除e0＜locj＜loce1。如果e0＜locj＜loce1，那么j必须为A的一些其他线程的成员，由引理4可知在线程thr1中e0和e1之间不存在发送动作，意味着随机数m在e1之前不会释放，这是AxiomF证明e1＜e0′所需要的部分。此外还必须证明e5′＜e2。这也可由AxiomF和引理4推断出，因为e2拥有n且n=New(e2′)在e5′之前不释放。

NSe⊨auth(I3,2)得证。 □

接下来，证明NSe⊨auth(R3,3)。

证明 假设诚实主体A≠B≠C且遵守Neuman-Stubblebine协议，并假设线程thr1是R3的一个实例。令e0＜loce1＜loc…＜loce5＜loce6为thr1上的动作，那么 e0, e1,…,e6的主体均为B。对一些atomsm,n,TB,s,s″,s‴有：

因为A、C都遵守Neuman-Stubblebine协议，动作e′、e″必须为协议基本序列中的一个实例成员。唯一一些包含Encrypt(_)动作的是I3、R1、R2、R3、S2，使用在证明时排除I3的方法，可以排除R1、R2、R3。接下来证明I3、S2。

如果e′或者e″是I3中的一个实例，那么对于一些atomsm1,n1,K1,TB1,s1′,s1′,s1′′和主体D、E，在主体A上存在事件e0′,e1′,e2′,e3′,e4′,e5′，有：

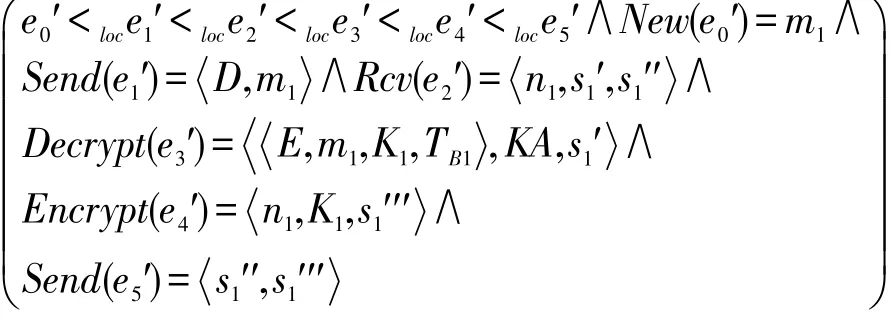
这样，又必须存在一个事件 e‴使得 e‴＜e3′∧DEMatch(e3′,e‴)∧loc(e‴)=B∨loc(e‴)=C成立。那么。

因为主体都遵守Neuman-Stubblebine协议，动作e‴必须为协议基本序列中的一个实例成员。唯一一些包含Encrypt(_)动作的是I3、R1、R2、R3、S2，与上文排除法相同，排除I3。

如果e‴是R1中的一个实例，那么对于一些atoms m2,n2,TB2,s2和主体F，在主体B上存在事件e0′′,e1′′, e2′′,e3′′，有：

明显不符合要求，排除R1。同理R2和R3排除。

如果e‴是S2中的一个实例，那么对于一些atoms m3,n3,K3,TB3,s3,s3′,s3′和主体G、H，在主体C上存在事件e0′′,e1′′,e2′′,e3′′,e4′′,e5′′，有：

即e3′′=e‴，因此有G=E,m3=m1,K3=K,TB3=TB1,s3′= s1′，得：

现在回过头来看e″，如果e″是也S2中的一个实例，那么对于一些atomsm4,n4,K4,TB4,s4,s4′,s4′和主体J、L，在主体C上存在事件e0′,e1′,…,e5′，有：

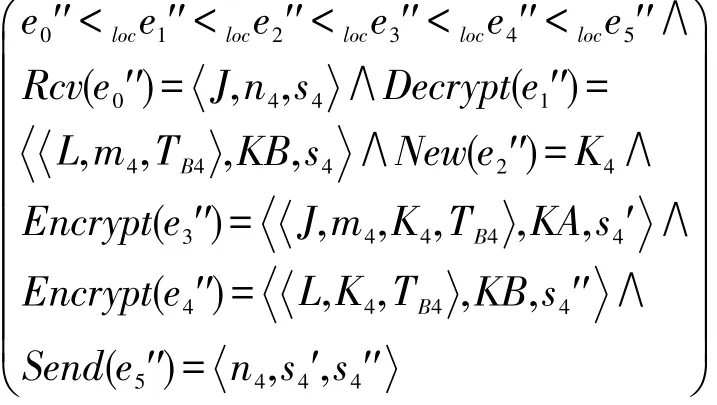
必须有Encrypt(e3′)=Encrypt(e″)或Encrypt(e4′)=Encrypt(e″)。

即e4′=e″，于是L=A,K4=K,TB4=TB,s4′=s″，因此有：

由引理4可知，m4=m，可得s4=s，有：

如果要证NSe⊨auth(R3,3)，就必须先证明有三对（强）匹配会话，而要证明（强）匹配会话，首先要有（强）匹配。即如果要证明NSe⊨auth(R3,3)，就必须有：

由式（6）、（7）、（9）不能证明A=D和m=m1，证明结束。 □

Neuman-Stubblebine协议只能证明第一个强认证性质，因此可以认为不符合强认证理论，存在消息重放的可能性，响应者是不安全的。说明Neuman-Stubblebine协议的初始认证阶段不能够达到双向身份认证，可能存在由于消息重放引起的类型攻击。

5 结束语

本文以事件逻辑为基础，定义强匹配及匹配会话，结合事件逻辑公理和推理规则，提出强认证理论。利用该理论对有3个主体的Neuman-Stubblebine协议进行研究，首先对协议基本序列进行合法定义，其次分别证明发送者和接收者的安全性。证明得出发送者是安全的而接收者是不安全的，不能达到双向身份认证，是不安全的协议，说明强认证理论适用于三方的网络安全协议。认证协议可以通过只对协议诚实主体动作的推理来证明其认证性，强认证理论适用于多个主体的网络安全协议认证性分析。

[1]Li Yan,Huang Guangqiu,Zhang Bin.Markov evolutionary game model for dynamic network attacks safety analysis[J]. Journal of Frontiers of Computer Science and Technology, 2016,10(9):1272-1281.

[2]Datta A,Derek A,Mitchell J C,et al.Protocol composition logic[J].Electronic Notes in Theoretical Computer Science, 2007,172:311-358.

[3]Constable R L.On building constructive formal theories of computation noting the roles of turing,church,and brouwer [C]//Proceedings of the 27th Annual IEEE Symposium on Logic in Computer Science,Dubrovnik,Croatia,June 25-28,2012.Piscataway,USA:IEEE,2012:2-8.

[4]Berg M.Formal verification of cryptographic security proofs[R]. Faculty of Natural Sciences and Technology,Department of Computer Science,Saarland University,2013.

[5]Lu Laifeng,Duan Xindong,Ma Jianfeng.Improvement and formal proof on protocol Otway-Rees[J].Journal on Communications,2012,33(S1):250-254.

[6]Bickford M,Constable R L.A logic of events,TR2003-1893[R]. Cornell University,2003.

[7]Bickford M,Constable R L.Automated proof of authentication protocols in a logic of events[C]//Proceedings of the 6th International Verification Workshop,Edinburgh,Jul 20-21,2010:13-30.

[8]Bickford M.Unguessable atoms:a logical foundation for security[C]//LNCS 5295:Proceedings of the 2nd International Conference on Verified Software:Theories,Tools and Experiments,Toronto,Canada,Oct 6-9,2008,Berlin,Heidelberg:Springer,2008:30-53.

[9]Bickford M,Constable R L.Formal foundations of computer security[J].NATO Science for Peace and Security Series, D:Information&Communication Security,2008,14:29-52.

[10]Liu Xinqian,Xiao Meihua,Cheng Daolei,et al.Security authentication of the modified Needham-Schroeder protocol based on logic of event[J].Computer Engineering&Science,2015,37(10):1850-1855.

[11]Chien H Y,Wu T C,Yeh M K.Provably secure gatewayoriented password based authenticated key exchange protocol resistant to password guessing attacks[J].Journal of Information Science&Engineering,2013,29(2):249-265.

[12]Xiao Meihua,Bickford M.Logic of events for proving security properties of protocols[C]//Proceedings of the 2009 International Conference on Web Information Systems and Mining,Shanghai,Nov 7-8,2009.Washington:IEEE Computer Society,2009:519-523.

[13]Xiao Meihua,Ma Chenglin,Deng Chunyan.A novel approach to automatic security protocol analysis based on authentication event logic[J].Chinese Journal of Electronics,2015,24 (1):187-192.

[14]Li Xiehua,Gao Chunming.Efficient protocol-proving algorithm based on improved authentication tests[J].Computer Science,2009,36(4):73-76.

[15]Ding Mengwei,Zhou Qinglei,Zhao Dongming.The strand space model of Neuman-Stubblebine protocol and its analysis[J].Computer Applications and Software,2009,26(5): 37-39.

附中文参考文献：

[1]李艳,黄光球,张斌.动态攻击网络Markov演化博弈安全分析模型[J].计算机科学与探索,2016,10(9):1272-1281.

[5]鲁来凤,段新东,马建峰.Otway-Rees协议改进及形式化证明[J].通信学报,2012,33(S1):250-254.

[10]刘欣倩,肖美华,程道雷,等.基于事件逻辑的改进Needham-Schroeder协议安全性证明[J].计算机工程与科学,2015, 37(10):1850-1855.

[14]李谢华,高春鸣.基于改进认证测试理论的高效安全协议验证算法[J].计算机科学,2009,36(4):73-76.

[15]丁萌伟,周清雷,赵东明.Neuman-Stubblebine协议的串空间模型及分析[J].计算机应用与软件,2009,26(5):37-39.

XIAO Meihua was born in 1967.He received the Ph.D.degree in computer software and theory from Institute of Software,Chinese Academy of Sciences in 2007.From 2008 to 2009,he worked as a visiting scholar at Cornell University.Now he is a professor and Ph.D.supervisor at School of Software,East China Jiaotong University.His research interests include information security and software formal method,etc.

肖美华（1967—），男，江西南昌人，2007年于中国科学院软件研究所计算机软件与理论专业获得博士学位，2008年至2009年于美国康奈尔大学做访问学者，现为华东交通大学教授、博士生导师，主要研究领域为信息安全，软件形式化方法等。

LIU Xinqian was born in 1990.She is an M.S.candidate at School of Software,East China Jiaotong University. Her research interests include information security and software formal method,etc.

刘欣倩（1990—），女，辽宁营口人，华东交通大学软件学院硕士研究生，主要研究领域为信息安全，软件形式化方法等。

LI Yanan was born in 1992.She is an M.S.candidate at School of Software,East China Jiaotong University. Her research interests include information security and software formal method,etc.

李娅楠（1992—），女，河南洛阳人，华东交通大学软件学院硕士研究生，主要研究领域为信息安全，软件形式化方法等。

CHENG Daolei was born in 1991.He is an M.S.candidate at School of Software,East China Jiaotong University. His research interests include information security and software formal method,etc.

程道雷（1991—），男，江西上饶人，华东交通大学软件学院硕士研究生，主要研究领域为信息安全，软件形式化方法等。

MEI Yingtian was born in 1992.She is an M.S.candidate at School of Software,East China Jiaotong University. Her research interests include information security and software formal method,etc.

梅映天（1992—），安徽池州人，华东交通大学软件学院硕士研究生，主要研究领域为信息安全，软件形式化方法等。

Security Certification of Three-Party Network Protocols Based on Strong Authentication Theory*

XIAO Meihua1,LIU Xinqian1,2+,LI Yanan1,CHENG Daolei1,MEI Yingtian1
1.School of Software,East China Jiaotong University,Nanchang 330013,China
2.Department of Information and Technology,PICC Property and Casualty Company Limited(Ningbo Branch), Ningbo,Zhejiang 315000,China
+Corresponding author:E-mail:liuxinqianlxq@sina.com

Formal method is an important approach for analyzing network security protocols.Network protocol security is a research hotspot in information security field.Event logic is a formalism for describing transition between states in a distributed system.It’s common to use event logic to certify the security of network security protocols. Based on event logic,this paper defines strong match and match sessions,and proposes the strong authenticationtheory by combining event logic axioms and inference rules.Using the strong authentication theory,this paper proves that three-principal Neuman-Stubblebine protocol is not secure because the sender is secure and the receiver isn’t secure.The research results show that the strong authentication theory is applicable to the security certification of similar multi-party security protocols.

formal method;event logic;strong authentication theory;Neuman-Stubblebine protocol

10.3778/j.issn.1673-9418.1607032

A

TP309

*The National Natural Science Foundation of China under Grant Nos.61163005,61562026(国家自然科学基金);the Natural Science Foundation of Jiangxi Province under Grant Nos.20132BAB201033,20161BAB202063(江西省自然科学基金);the Science and Technology International Cooperation Project of Jiangxi Province under Grant No.20151BDH80005(江西省对外科技合作技术项目);the Soft Science Research Project of Jiangxi Province under Grant No.20151BBA10042(江西省软科学研究计划项目);the Science and Technology Ground Project of College in Jiangxi Province under Grant No.KJLD13038(江西省高校科技落地计划项目);the Program of Co-Innovation Center of the Intelligent Management and Equipment for Orchard on the Hilly Land in South China (南方山地果园智能化管理与装备协同创新中心资助项目);the Special Funds for Visiting Scholars Development Plan of the Young Teachers in the Ordinary Universities of Jiangxi Province(江西省普通本科高校中青年教师发展计划访问学者专项资金).

Received 2016-07,Accepted 2016-09.

CNKI网络优先出版:2016-09-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160908.1045.020.html