基于GDA的置信规则库参数训练的集成学习方法*
吴伟昆,傅仰耿,苏 群,吴英杰,巩晓婷
1.福州大学 数学与计算机科学学院,福州 350116
2.福州大学 经济与管理学院,福州 350116
基于GDA的置信规则库参数训练的集成学习方法*
吴伟昆1,傅仰耿1,苏 群1,吴英杰1,巩晓婷2+
1.福州大学 数学与计算机科学学院,福州 350116
2.福州大学 经济与管理学院,福州 350116
WU Weikun,FU Yanggeng,SU Qun,et al.GDA based ensemble learning methods for parameter training in belief rule base.Journal of Frontiers of Computer Science and Technology,2016,10(12):1651-1661.
置信规则库(BRB);集成学习;梯度下降法(GDA);Bagging;AdaBoost
1 引言
随着信息技术的快速发展,为了能够处理在各种复杂应用背景下多样性、大容量、高速、实时的数据,信息融合(data fusion)技术越来越受到各个领域专家的重视。信息融合是模仿人类处理信息的结果,它实际上是一个不确定性推理与决策的过程,其方法包括贝叶斯概率推理法、D-S(Dempster-Shafter)证据理论[1-2]、模糊推理[3]、神经网络法[4]等。对于实际应用中数据存在模糊不确定性、不完整性或概率不确定性以及非线性特征的问题,基于置信度理论的推理方法充分展示了其优越性[5]。
Yang等人[6]在D-S证据理论、决策理论[7]、模糊理论和传统IF-THEN规则库[8]的基础上提出了基于证据推理的置信规则库推理方法(belief rule base inference methodology using the evidential reasoning approach,RIMER)。通过对传统IF-THEN规则库的扩展而得到的置信规则库(belief rule base,BRB)系统,目前已成功应用于军事能力评估[9]、石墨成分检测[10]、输油管道检漏[11]等领域。
现有对BRB的研究主要针对单个BRB系统进行,单个BRB系统的推理性能不仅受规则库参数的取值影响,还受参与训练的数据集影响。Yang等人[10]通过选取对应的输入输出作为训练数据对BRB系统进行参数学习,从而确定规则库参数的具体取值;Liu等人[12]则根据数据集对初始BRB系统进行构建及训练;Su[13]和Wang等人[14]分别提出基于粒子群算法、专家干预策略与差分进化算法结合的参数训练方法,但未提出合理选择训练数据的方法,使得单个BRB系统的推理性能存在不稳定性。在上述方法中规则库训练集质量对BRB系统的推理性能起着关键的作用。训练数据量较少或抽取不均匀易导致BRB系统的参数训练不全面,推理能力下降,当面对复杂且规模较大的决策问题时,BRB系统的推理性能与规则库参数的取值密切相关[15],参数取值的细小差异都可能使BRB系统推理的结果出现明显差异。
鉴于此,本文结合Bagging算法[16]和AdaBoost算法[17-18]将BRB系统与集成学习相结合,通过加速梯度求法[19]对单个BRB系统进行参数训练,并对得到的多个BRB子系统进行集成,进而提升BRB系统的推理能力。在实验分析中,通过引入输油管道检漏的实验,分析本文BRB的Bagging集成方法对于动态特性曲线的拟合效果和推理性能,并与其他单个BRB系统进行比较。在多峰函数的实例中,分析BRB的AdaBoost集成方法在寻优能力和推理性能上的表现,并与其他单个BRB系统进行比较,说明本文方法的有效性。第2章简要介绍BRB系统和集成学习相关的理论知识,并提出本文拟解决的问题;第3章引入Bagging算法和AdaBoost算法,并分别与BRB系统的参数训练相结合,提出解决现有问题的集成学习方法;第4章通过两个实例分析置信规则库系统集成学习方法的有效性;最后对本文进行总结,并指出进一步的工作方向。
2 相关理论基础及问题提出
2.1BRB的表示及RIMER方法
2.1.1 BRB的表示
BRB中的置信规则是由传统的IF-THEN扩展而来,相比传统的IF-THEN规则,置信规则中新增分布式置信框架、前提属性权重和规则权重,其中第k条规则表示如下:

其中,Rk(k=1,2,…,L)表示第k条规则,L表示规则的总条数;表示第k条规则的第i个前提属性的参考值,Tk表示第k条规则中前提属性的个数;Dj(j=1,2,…,N)表示规则结果评价等级的集合,N为集合大小;表示第k条规则的结果输出在第 j个评价等级Dj上的置信度;当时,表示第k条规则包含完整的信息,否则说明第k条规则中的信息是不完整的。此外,第k条规则的规则权重为θk(k=1,2,…,L),表示第k条规则相对BRB中其他规则的重要程度;前提属性的权重为δk,i(k=1,2,…,L,i=1,2,…,Tk),反映了第i个前提属性相对其他前提属性的重要度。
2.1.2 RIMER方法
RIMER方法是BRB系统的核心内容,其在规则推理时主要包含3个步骤:首先是激活权重的计算,然后是置信度的修正,最后再使用证据推理(evidential reasoning,ER)算法合成激活规则。
激活权重的计算取决于输入数据、前提属性权重和规则权重,进行计算之前要先计算前提属性在每个参考值上的个体匹配度。假设BRB的输入xi(i=1,2,…,M)为数值形式,则由xi和前提属性参考值集合,根据效用的信息转化[20],可得第k条规则中第i个输入相对于参考值的个体匹配度的计算方式为:

则第k条规则的激活权重的计算公式为:

其中,ωk∈[0,1],k=1,2,…,L。
当输入数据包含模糊、不确定数据时,需要对结果部分的各评价等级的置信度进行修正,第k条规则的第i个评价等级Di的置信度βˉi,k修正公式为:

其中,|At|表示候选值的个数,如果输入数据是完整的,则。
在ER算法中,Wang等人[21]提出了ER解析算法对BRB中所有的规则进行组合,BRB的最终输出f(x)可表示为:

其中βj表示相对于评价结果Dj的置信值,且

假设μ(Dn)表示第n个评价等级Dn的效用值,则BRB系统的数值型输出的最终表示为:

2.2 集成学习方法
在回归问题或分类问题中,学习机在特征空间中不同区域的性能存在差异,单一学习机容易造成较多的错误预测,对于某个学习机预测错误的区域,运用其他学习机有可能得到正确的结果,实现学习机之间的模式互补。集成学习技术利用多个学习机来解决同一个问题,它通过回归或分类算法获取多个不同的学习机,然后通过某种方式将得到的多个学习机进行组合,从而提高学习系统的预测能力。
从学习机的构建方式可将集成学习大致分为两种:一种是学习机之间的依赖关系较弱,可并行生成的算法,如Bagging算法、随机森林算法等;另一种是学习机之间依赖关系较强,必须串行生成的算法,如AdaBoost算法。并行集成学习算法的每个学习机之间的输出是独立的。串行集成学习的算法在构造过程中前后学习机存在依赖关系,即当前学习机的构建是在之前学习机训练后的基础上进行的,学习机存在次序关系。经过后一个学习机的训练能够有效消除前一个学习机在输出上的错误率和对各个学习机性能不一致的影响。在进行学习机的组合时运用最广泛的是简单投票法、加权投票法。
2.3 问题提出
置信规则库系统的推理准确性不仅与参数的取值息息相关,还受到训练数据集的影响。BRB系统的参数学习是一种监督学习,通过参数学习得到的参数取值能使BRB系统对训练数据具有较好的推理能力。理想的训练数据集可使BRB系统具有良好的稳定性和推理性能,而当BRB系统的训练集数据存在分布不均或数据量较少时,易导致参数训练不全面,使得训练得到的单个BRB系统推理结果提供的决策信息存在局部性,不能很好地预测实际系统的输出。在解决规模较大且复杂的决策问题时,BRB系统的参数取值对最终系统的推理能力有着关键的影响[15],参数的取值即使存在细小的差异都可能使BRB系统得到两种差别很大的结果。
为解决现有的问题,本文提出了置信规则库的集成学习方法,分别将BRB与Bagging算法的数据重抽取技术和AdaBoost提升算法相结合,在文献[19]的基础上进行BRB子系统的参数学习,并对得到的多个BRB子系统进行集成。
3 BRB参数训练的集成学习方法
3.1 置信规则库参数训练方法
梯度下降法(gradient descent algorithm,GDA)是一种求解问题最优化的算法,现广泛应用于求解无约束优化问题,其中相关的改进算法包括共轭梯度法、Wolf简约梯度法、广义简约梯度法等[22]。在对置信规则库系统(即学习机)进行集成学习时,本文将加速梯度求法[19]作为学习算法对学习机进行训练。
假设待求解的优化函数为ξ(P),P为BRB中待优化的参数集合,且这些参数带有约束条件。
算法1使用梯度下降法进行BRB的参数训练

3.2 置信规则库的Bagging集成学习方法
Bagging是Breiman在1996年提出的一种基于数据重复抽样技术[23]bootstrap sampling)的算法。在训练阶段,各学习机的训练集由原始训练集利用重抽取技术获得。假设给定的数据集包含n个样本。对数据集有放回地抽样n次,产生包含n个样本的训练集。这样,原始训练集中的某个样本在某个训练集中可能出现多次或根本不出现。显然每个样本被选中的概率是1/n,因此未被选中的概率为(1-1/n),则一个样本在某个训练集中一次都未出现的概率为(1-1 n)n。当n趋于无穷大时,这一概率趋近于e-1=0.368,即训练集中的样本大概占原来数据集的63.2%。
在对Bagging算法得到的多个学习机进行组合时,对于分类问题可选择多数投票法,而对于回归问题,由于多个学习机的输出在空间中是离散分布的点,通过聚类方式对输出的分布进行分析,计算聚类结果中类成员最多的类,其类中心作为最终的输出。本文通过聚类的方式模拟多数投票策略,并采用K-means聚类算法对多个学习机的结果进行集成。
K-means算法步骤如下:
(1)初始化数据集dataset,设置k值;
(2)随机选取k个数据点作为聚类中心;
(3)由相似度距离公式,将所有数据点归到离其最近的聚类;
(4)根据聚类结果,计算新的聚类中心;
(5)所有数据点根据新的聚类中心重新聚类;
(6)重复(4)、(5),直到聚类中心没有发生变化,算法结束,输出结果。
假设参与集成的BRB个数为M,则数据集dataset由GDA训练后的M个BRB在每个测试数据上的预测结果组成,即一个测试数据对应M个预测结果。本文在K-means算法中,聚类中心个数k取,以绝度误差和作为相似度距离公式。
算法2 BRB的Bagging集成学习


BRB的Bagging集成学习流程如图1所示。

Fig.1 BRB-ensemble process using Bagging图1 BRB的Bagging集成学习流程
3.3 置信规则库的AdaBoost集成学习方法
AdaBoost是最优秀的Boosting算法之一,被评为数据挖掘十大算法之一[24]。Freund和Schapire在1997年提出了基于回归模型的AdaBoost.R算法[17],Drucker最早将Boosting算法的回归模型应用到实际问题中[25],将AdaBoost.R进行改进得到AdaBoost.R2,并应用到回归问题中。AdaBoost.R2与AdaBoost.R类似,算法初始阶段对每个训练样本赋予相等的权重1/n,其核心内容是维护训练集样本的权值分布,每一轮迭代对预测错误的样本赋以较大的权重,使得下一个学习机在训练时集中对比较难预测的样本进行学习。通过多次迭代得到多个不同学习机及其权重,学习机权重越小则说明其预测效果越好。最终对多个学习机进行集成时,对于分类问题可使用加权投票策略,而回归问题则可采用加权平均的方式进行组合。
AdaBoost算法不同于Bagging算法,其在训练时是串行进行的,而Bagging是并行运行的。AdaBoost算法中第k个学习机训练时关注的是前k-1个学习机中错误预测的样本,并加大取这些样本的概率,而Bagging算法是随机抽取的。
算法3 BRB的AdaBoost集成学习

BRB的AdaBoost集成学习的流程如图2所示。

Fig.2 BRB-ensemble process usingAdaBoost图2 BRB的AdaBoost集成学习的流程
4 实验结果与分析
为验证置信规则库与集成学习方法相结合的有效性,本文从算法的收敛精度和曲线拟合效果进行实验分析,并分别在输油管道检漏和多峰函数两个实例中将本文方法与单个BRB系统进行比较。此外,实验环境为:Intel®Core i5-4570 CPU@3.20 GHz,4 GB内存,Windows 10操作系统;算法由Visual Studio 2013编写。
4.1 输油管道检漏
管道检漏问题中以安装在英国一条100多公里长的输油管道作为研究对象,当管道发生泄漏时,管道中油液的油液流量(FlowDiff,FD)和压力(Pressure-Diff,FD)会按一定的模式发生变化,进而影响泄漏大小(LeakSize,LS)。因此将流量和压力作为BRB系统的输入,泄漏大小作为BRB系统的输出。
构建BRB系统时FD和PD满足如下条件:以FD和PD作为BRB系统的前提属性,FD含8个参考值,PD含7个候选,即FD∈{1 0,5,3,1,0,1,2,3} ,PD∈{0.042,0.025,0.01,0,0.01,0.025,0.042},而输出LS分为5个评价等级,即D={0,2,4,6,8}。
在泄漏测试中,每10 s作为一个周期收集2 008组从正常到发生25%泄漏(即当管道中流动100吨油液时有25吨发生泄漏)时的实时数据。
图3是管道检漏初始BRB系统[9]对真实泄漏曲线的拟合效果。

Fig.3 Fitting effect of initial BRB of pipeline leak detection图3 管道检漏初始BRB系统的拟合效果
在进行BRB的Bagging集成学习实验时,以2 008组数据为初始样本进行boostrap数据重抽取,得到最终的测试集,BRB数量T=25。经过25轮训练后,对训练后的BBR通过K-means算法进行组合输出,如图4和图5,是集成系统在测试集上均方误差(mean square error,MSE)、皮尔森相关系数[26]Pearson correlation coefficient,PCC)随着参与集成的BRB数量增加而变化的曲线。
从图4和图5中可以发现,随着参与集成的BRB子系统数量的增加,集成系统的MSE不是单调递减,而是整体呈现一种下降的趋势,PCC值也是整体呈上升的趋势,说明通过BRB的Bagging集成学习能够在收敛精度和泛化能力上往好的方向发展。

Fig.4 MSE of Bagging ensemble learning system with the amount of BRB图4 Bagging集成学习系统MSE随BRB数量变化的曲线

Fig.5 PCC of Bagging ensemble learning system with the amount of BRB图5 Bagging集成学习系统PCC随BRB数量变化的曲线
当参与集成的BRB子系统为20时,集成系统对真实系统输出曲线的拟合效果如图6所示。
由图6可知,集成系统能够很好地拟合真实系统的动态输出,图中波动较大的点是由于数据中噪音点的影响。为了进一步分析BRB的Bagging集成系统在收敛精度和泛化能力上的表现,将本文方法与其他单个BRB系统进行比较,以均方误差、皮尔森相关系数作为衡量指标,结果如表1所示。

Fig.6 Fitting effect of Bagging ensemble system of pipeline leak detection图6 管道检漏中Bagging集成系统的拟合效果

Table 1 Comparison on reasoning performance of Bagging ensemble system with single BRB system表1 Bagging集成系统与单个BRB系统推理性能比较
从表1中MSE值可知,BRB的Bagging集成系统相对粒子群算法[13]、基于加速梯度求法[19]的单个BRB系统具有更高的收敛精度。Fmincon函数方法虽有较高的收敛精度,但其依托于Matlab软件,可移植性差。由表1分析,BRB的Bagging集成学习求得的PCC值优于单个BRB系统,说明其对真实系统输出的动态变化进行预测时结果更准确,有更好的推理性能。
4.2 多峰函数拟合
为验证集成学习方法具有较好的寻优能力和收敛精度,引入多峰函数[27],其表达式如下:

构建BRB系统时,根据函数曲线各个极值点的函数值设定规则,结果集的评级等级和等级效用值为{D1,D2,D3,D4,D5}={-0.5,0,0.5,1.0,1.5},变量x作为前提属性,其属性参考值为{-5,-2,0,2,5}。依据规则的信息转换技术[6]对规则结果集的置信度进行初始化,初始的BRB如表2所示。

Table 2 Initial BRB of multimodal function表2 多峰函数初始BRB
初始BRB拟合多峰函数的曲线及误差曲线如图7所示。

Fig.7 Fitting effect of initial BRB of multimodal function图7 多峰函数初始BRB拟合效果
进行BRB的AdaBoost集成学习实验时,在多峰函数输入变量x的取值区间[-5,5]上选取10 000个数据作为总体样本,并均匀选取1 000个点作为训练数据,BRB数量T=25,即进行25次的AdaBoost迭代训练。
经过AdaBoost的T次迭代训练和数据误差权重的更新后,可得到T个训练后的BRB子系统,每个子系统带有各自的权重α,根据加权平均法进行集成。图8、图9是集成系统在测试集上均方根误差(root mean square error,RMSE)和PCC随着参与集成的BRB数量的增加而变化的曲线。
由图8和图9分析可知,随着参与集成的BRB个数的增加,集成系统的收敛精度呈现不断下降的趋势,PCC值呈现逐渐上升的趋势,说明集成系统对真实系统的预测效果越来越好。而随着BRB个数的增加,两条曲线趋于平稳,即集成系统的推理性能较稳定。
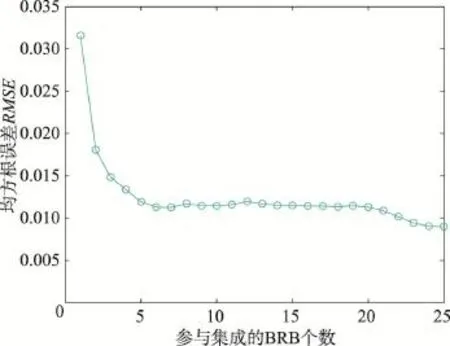
Fig.8 RMSE ofAdaBoost ensemble learning system with the amount of BRB图8 AdaBoost集成学习系统RMSE随BRB数量变化的曲线

Fig.9 PCC ofAdaBoost ensemble learning system with the amount of BRB图9 AdaBoost集成学习系统PCC随BRB数量变化的曲线
图10是在T=25时集成系统对多峰函数曲线真实输出的拟合效果以及预测值与实际值之间的误差曲线。
从图10可知,集成系统能够很好地拟合多峰函数的真实曲线,且误差曲线浮动较小。为了分析BRB的AdaBoost集成系统在收敛精度和推理性能上的表现,将其与Matlab中的Fmincon优化函数、常瑞的梯度法[28]、差分进化算法[14]的单个BRB系统训练方法进行比较,如表3所示,以RMSE、PCC作为衡量指标。
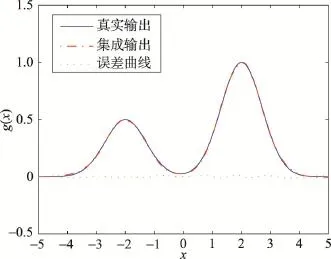
Fig.10 Fitting effect ofAdaBoost ensemble system of multimodal function图10 多峰函数中AdaBoost集成系统的拟合效果

Table 3 Comparison on reasoning performance of AdaBoost ensemble system with single BRB system表3 AdaBoost集成系统与单个BRB系统推理性能比较
由表3可知,BRB的AdaBoost集成系统相对差分进化算法和常瑞基于梯度法的单个BRB系统具有更好的收敛精度和推理性能。Fmincon函数虽然也得到了较好的结果,但其依赖于Matlab,不易移植且耗时,训练时长约400 s,而BRB的AdaBoost集成学习只需约60 s。
5 结束语
本文针对单个BRB系统在训练集数据分布不均或数据量较少的情况下易出现推理性能下降的问题,将Bagging算法和AdaBoost算法分别与BRB系统进行结合,在BRB的Bagging集成学习中采用K-means算法进行集成。通过输油管道实验的结果表明,集成系统能够很好地拟合具有动态特性的曲线,与其他单个BRB系统进行比较,结果说明本文方法具有较高的收敛精度和推理性能。在BRB的Ada-Boost集成学习中采用加权平均法进行集成,多峰函数的实验结果表明,集成系统具有较好的寻优能力和收敛速度。随着参与集成的BRB子系统的增加,所需存储空间将不断增加,收敛效率也会受到影响,因此进一步的研究方向是实现有选择性的集成,并将置信规则库的集成学习应用到分类问题中。
[1]Dempster A P.A generalization of Bayesian inference[J]. Journal of the Royal Statistical Society:Series B(Methodological),1968,30(2):205-247.
[2]Glenn S.A mathematical theory of evidence[M].Princeton, USA:Princeton University Press,1976.
[3]Zadeh L Z.Fuzzy sets[J].Information and Control,1965,8 (3):338-353.
[4]McCulloch W S,Pitts W.A logical calculus of the ideas immanent in nervous activity[J].The Bulletin of Mathematical Biophysics,1943,5(4):115-133.
[5]Miao Yangzi,Fang Jian,Ma Xiaoping.D-S evidence theory of fusion technology and application[M].Beijing:Publishing House of Electronics Industry,2013.
[6]Yang Jianbo,Liu Jun,Wang Jin,et al.Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J].IEEE Transactions on Systems,Man,and Cybernetics:PartASystems and Humans,2006,36(2):266-285.
[7]Hwang C,Yoon K.Methods for multiple attribute decision making[M].Heidelberg,Berlin:Springer-Verlag,1981:58-191.
[8]Sun R.Robust reasoning:integration rule-based and similaritybasedreasoning[J].ArtificialIntelligence,1995,75(2):241-295.
[9]Jiang Jiang,Li Xuan,Zhou Zhijie,et al.Weapon system capability assessment under uncertainty based on the evidential reasoning approach[J].Expert Systems with Applications,2011,38(11):13773-13784.
[10]Yang Jianbo,Liu Jun,Xu Dongling,et al.optimization models for training belief-rule-based systems[J].IEEE Transactions on Systems,Man and Cybernetics:Part A Systems and Humans,2007,37(4):569-585.
[11]Zhou Zhijie,Hu Changhua,Yang Jianbo,et al.Online updating belief-rule-based system for pipeline leak detection under expert intervention[J].Expert Systems with Applications,2009,36(4):7700-7709.
[12]Liu Jun,Martinez L,Calzada A,et al.A novel belief rule base representation,generation and its inference methodology[J].Knowledge-Based Systems,2013,53:129-141.
[13]Su Qun,Yang Longhao,Fu Yanggeng,et al.Parameter training approach based on variable particle swarm optimization for belief rule base[J].Journal of Computer Applications,2014, 34(8):2161-2165.
[14]Wang Hanjie,Yang Longhao,Fu Yanggeng,et al.Differential evolutionary algorithm for parameter training of belief rule base under expert intervention[J].Computer Science, 2015,42(5):88-93.
[15]Zhou Zhijie,Yang Jianbo,Hu Changhua,et al.Belief rule base expert system and complex system modeling[M].Beijing:Science Press,2011:1-119.
[16]Breiman L.Bagging predictors[J].Machine Learning,1996, 24(2):123-140.
[17]Freund Y,Schapire R E.A decision-theoretic generalization of on-line learning and an application to boosting[J].Journal of Computer and System Sciences,1997,55(1):119-139.
[18]Freund Y,Schapire R E.Experiments with a new boosting algorithm[C]//Proceedings of the 13th International Conference on Machine Learning,Bari,Italy,Jul 3-6,1996,San Francisco,USA:Morgan Kaufmann Publishers Inc,1996: 148-156.
[19]Wu Weikun,Yang Longhao,Fu Yanggeng,et al.Parameter training approach for belief rule base using the accelerating of gradient algorithm[J].Journal of Frontiers of Computer Science and Technology,2014,8(8):989-1001.
[20]Yang Jianbo.Rule and utility based evidential reasoning approach for multi-attribute decision analysis under uncertainties[J].European Journal of Operational Research,2001, 131(1):31-61.
[21]Wang Yingming,Yang Jianbo,Xu Dongling,et al.The evidential reasoning approach for multiple attribute decision analysis using interval belief degrees[J].European Journal of Operational Research,2006,175(1):35-66.
[22]Ma Changfeng.Optimization method and Matlab programming[M].Beijing:Science Press,2010:47-189.
[23]Efron B,Tibshirani R J.An introduction to the bootstrap [M].Boca Raton,USA:CRC Press,1994.
[24]Wu Xindong,Kumar V,Quinlan J R,et al.Top 10 algorithms in data mining[J].Knowledge and Information Systems,2008, 14(1):1-37.
[25]Drucker H.Improving regressors using boosting techniques[C]//Proceedings of the 14th International Conference on Machine Learning,Nashville,USA,Jul 8-12,1997.San Francisco, USA:Morgan Kaufmann Publishers Inc,1997:107-115.
[26]Hao Liren.SPSS practical statistics[M].Beijing:China Water&Power Press,2003.
[27]Chen Yuwang,Yang Jianbo,Xu Dongling,et al.On the inference and approximation properties of belief rule based systems[J].Information Sciences,2013,234:121-135.
[28]Chang Rui,Wang Hongwei,Yang Jianbo.An algorithm for training parameters in belief rule-bases based on the gradient and dichotomy methods[J].Systems Engineering,2007, 6(6):287-291.
附中文参考文献:
[5]缪燕子,方健,马小平,等.D-S证据理论融合技术及其应用[M].北京:电子工业出版社,2013.
[13]苏群,杨隆浩,傅仰耿,等.基于变速粒子群优化的置信规则库参数训练方法[J].计算机应用,2014,34(8):2161-2165.
[14]王韩杰,杨隆浩,傅仰耿,等.专家干预下置信规则库参数训练的差分进化算法[J].计算机科学,2015,42(5):88-93.
[15]周志杰,杨剑波,胡昌华,等.置信规则库专家系统与复杂系统建模[M].北京:科学出版社,2011:1-119.
[19]吴伟昆,杨隆浩,傅仰耿,等.基于加速梯度求法的置信规则库参数训练方法[J].计算机科学与探索,2014,8(8): 989-1001.
[22]马昌凤.最优化方法及其Matlab程序设计[M].北京:科学出版社,2010:47-189.
[26]郝黎仁.SPSS实用统计分析[M].北京:中国水利水电出版社,2003.

WU Weikun was born in 1991.He is an M.S.candidate at College of Mathematics and Computer Science,Fuzhou University.His research interests include intelligent decision technology,data mining and ensemble learning,etc.
吴伟昆(1991—),男,福建泉州人,福州大学数学与计算机科学学院硕士研究生,主要研究领域为智能决策技术,数据挖掘,集成学习等。

FU Yanggeng was born in 1981.He received the Ph.D.degree from Fuzhou University in 2013.Now he is an associate professor at College of Mathematics and Computer Science,Fuzhou University,and the member of CCF.His research interests include multi-criteria decision making under uncertainty,belief rule base inference and mobile internet applications,etc.
傅仰耿(1981—),男,福建泉州人,2013年于福州大学获得博士学位,现为福州大学数学与计算机科学学院副教授,CCF会员,主要研究领域为不确定多准则决策,置信规则库推理,移动互联网应用等。

SU Qun was born in 1991.He is an M.S.candidate at College of Mathematics and Computer Science,Fuzhou University.His research interests include intelligent decision making technology and belief rule base inference,etc.
苏群(1991—),男,福建宁德人,福州大学数学与计算机科学学院硕士研究生,主要研究领域为智能决策技术,置信规则库推理等。

WU Yingjie was born in 1979.He received the Ph.D.degree from Southeast University in 2012.Now he is a professor at College of Mathematics and Computer Science,Fuzhou University.His research interests include data mining, data security and privacy preservation,etc.
吴英杰(1979—),男,福建泉州人,2012年于东南大学获得博士学位,现为福州大学数学与计算机科学学院教授,主要研究领域为数据挖掘,数据安全与隐私保护等。

GONG Xiaoting was born in 1982.She received the M.S.degree from Fuzhou University in 2006.Now she is a lecturer at College of Economics and Management,Fuzhou University.Her research interests include multi-criteria decision making under uncertainty and information hiding technology,etc.
巩晓婷(1982—),女,河南漯河人,2006年于福州大学获得硕士学位,现为福州大学经济与管理学院讲师,主要研究领域为不确定多准则决策,信息隐藏技术等。
GDA Based Ensemble Learning Methods for Parameter Training in Belief Rule Base*
WU Weikun1,FU Yanggeng1,SU Qun1,WU Yingjie1,GONG Xiaoting2+
1.College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,China
2.College of Economics and Management,Fuzhou University,Fuzhou 350116,China
+Corresponding author:E-mail:xtgong@126.com
Current research on belief rule base(BRB)focuses on single BRB system,however,the reasoning performance of single BRB system is influenced by the values of parameters.And the uneven distribution or small amount of training data can lead to the incompleteness of training parameters,which makes the locality of information for decision provided by reasoning results.To solve these problems,this paper proposes BRB-ensemble system base in gradient descent algorithm(GDA)via combining the Bagging and AdaBoost with BRB respectively,and the BRB system is applied to the pipeline leak detection and multimodal function fitting.The performance of BRB system can be improved by the integration of multiple sub-BRB.In the case study,the convergence accuracy and fitting effect are used to analyze the performance of BRB-ensemble,and the proposed approach is compared with other single BRB system. The experimental results show that the BRB-ensemble method is reasonable and effective.
belief rule base(BRB);ensemble learning;gradient descent algorithm(GDA);Bagging;AdaBoost
10.3778/j.issn.1673-9418.1605043
A
TP18
*The National Natural Science Foundation of China under Grant Nos.61300026,71501047(国家自然科学基金);the Natural Science Foundation of Fujian Province under Grant No.2015J01248(福建省自然科学基金);the Science and Technology Development Foundation of Fuzhou University under Grant Nos.2014-XQ-26,14SKF16(福州大学科技发展基金).
Received 2016-05,Accepted 2016-07.
CNKI网络优先出版:2016-07-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160701.1646.004.html
摘 要:目前对置信规则库(belief rule base,BRB)的研究主要针对单个BRB系统,然而单个BRB系统的推理性能不仅受参数取值的影响,而且当训练集分布不均衡或数据量较少时,容易导致参数训练不全面,从而使得推理结果所提供的决策信息存在局部性。通过引入Bagging算法和AdaBoost算法,分别与BRB相结合提出了基于梯度下降法(gradient descent algorithm,GDA)的置信规则库系统的集成学习方法,并分别应用于输油管道检漏、多峰函数的置信规则库训练,将多个BRB子系统集成,提高系统的推理性能。在实验中,以收敛精度和曲线拟合效果作为衡量指标来分析集成系统的性能,并将集成系统与其他单个BRB系统进行比较,实验结果表明BRB集成学习方法合理有效。

