改进交互式蚁群算法及其应用*

黄永青，杨善林，梁昌勇

1.合肥工业大学 管理学院，合肥 230009

2.铜陵学院 信息技术与工程管理研究所，安徽 铜陵 244000

改进交互式蚁群算法及其应用*

黄永青1,2+，杨善林1，梁昌勇1

1.合肥工业大学 管理学院，合肥 230009

2.铜陵学院 信息技术与工程管理研究所，安徽 铜陵 244000

HUANG Yongqing,YANG Shanlin,LIANG Changyong.Improved interactive ant colony algorithm and its application.Journal of Frontiers of Computer Science and Technology,2016,10(12)：1720-1728.

交互式蚁群优化（interactive ant colony optimization，iACO）是一种利用人来评价解的优劣而进行系统优化的技术，可以求解性能指标不能或者难以数量化的优化问题。分析了交互式蚁群优化模型面临的研究困难。针对Tanabe等人提出的交互式蚂蚁算法性能不足的问题，提出利用全局历史最优解进行信息素的更新，并将信息素限定在一定区间内的改进交互式蚁群优化算法，从人机交互角度讨论了解的构造方法和人的评价策略。最后，利用函数优化和汽车造型设计进行了实验，运行结果表明算法具有较高优化性能。

交互式蚁群优化；蚁群优化；人机交互；汽车造型

1 引言

蚁群优化（ant colony optimization，ACO）自意大利学者Dorigo提出以来，已经应用于求解TSP（traveling salesman problem）等NP难问题[1]，并应用于二分社区网络挖掘[2]和记忆式图像检索[3]等领域。然而，这些传统的ACO算法需要建立显式的目标函数才能求解，当性能指标难以数量化时，算法应用受到限制。

交互式进化计算（interactive evolutionary computation，IEC）通过人来评价解对应的系统输出以确定解的优劣，而以进化算法在参数空间中搜索更好的解，已经成功应用于汽车造型设计[4]、基于搜索的软件工程[5]、产品形态设计[6]、图书商品个性化搜索[7]、协同产品定制[8]等方面。但IEC需要人不断参与进化过程进行解的评价，一般要求种群规模和进化代数处在一个较小水平；由于人评价具有不确定性，且其偏好会随着评价过程的进行而调整改变，这些因素制约了人机系统的求解性能。因此，IEC的改进、用户疲劳问题和用户评价的不确定性等成为研究热点。巩敦卫等人[9]根据组成个体各基因意义单元值出现的频率定义个体的相似度，可以在提高种群规模情况下适当减轻用户疲劳感，从而使得算法具有较高的搜索性能。另外，还可通过使用符合用户认知规律的区间数评价进化个体适应值[10]和代理模型等[11-12]方式，来解决以上问题。但是，目前IEC的搜索算法部分大多集中在遗传算法。

近几年来，交互式蚁群优化（interactive ant colony optimization，iACO）的研究为拓展IEC和传统ACO研究提供了新的思路[13-15]。iACO是一种进化个体适应值由人来评价的蚁群优化方法，由于利用蚂蚁进行解的构造和其独特的信息素更新方式，从而可获得满意的求解性能。

在IEC领域，对iACO的研究才刚刚起步，文献[13]研究了一种交互式蚂蚁算法模型，利用每一代中较好的2～3个解进行信息素的更新，并应用于成套服装的选择。作为一种实用的IEC技术，Tanabe等人是国外IEC领域最早[13]研究iACO模型的作者。文献[14]则针对软件工程中早期设计问题，提出一种构造“属性、方法和类”的iACO方法，可以对信息系统中的类及其含有哪些属性和方法进行设计。文献[15]也提出一种iACO模型，并应用于汽车造型设计。

由于iACO是近几年发展的模型，有必要分析iACO模型研究面临的挑战问题，并针对文献[13]中的iACO算法存在着易陷入局部优化、性能偏低的问题，给出本文的改进iACO模型。

2 iACO模型研究的挑战

在传统ACO模型中，蚂蚁群体的规模大，迭代步数多，其求解性能较优。而在iACO模型中，受到人的评价能力（人容易疲劳）、显示器展示个体表现型数目或系统输出的特殊性（如音频个体）等因素的影响，蚂蚁数目一般只有几个至20个个体，迭代步数也只有十多步或几十步，因此在这种苛刻条件下，使得iACO模型具有满意的求解性能是研究者面临的巨大挑战。一些提高iACO模型的策略被采用，如要求当前代构造的解均不同[15]，或者新构造的解与之前构造的所有解均不同[13]。另外，一些传统ACO算法的各种改进策略对iACO模型性能的提高有正面的作用，如将信息素限制在适当的区间内[14]。

类似于IEC，iACO用户疲劳问题也是广大研究者面临的核心问题。在IEC中，用户不断地打分和比较分值相近（如70分与71分）个体之间的差异，会使用户容易疲劳。显然，IEC克服用户疲劳问题的相关研究，会对iACO模型研究有着很好的借鉴意义。其实，由于iACO模型自身的特点，使得用户有时不必给出进化个体具体的评价值，而只需指出用户满意的解或判定当前最好解即可[13,15]，这大大减小了用户的评价疲劳。

iACO模型构造出来后，会利用某个应用领域的实际问题进行性能测试。但这些问题常常有较强的实践背景，因此在IEC领域还缺乏基准的测试问题或案例，来评估这些交互式算法的性能。例如，在基于搜索的软件工程领域，由于缺乏基准的软件设计问题，Smith等人[14]利用自己设计的3个不同规模问题进行算法性能的测试。文献[15]通过构造一个标准测试函数来评估算法性能，为设计标准测试案例提供了思路。另外，通过问卷，与以往算法结果进行比较，也可以测试和了解算法的性能与有效性。

最优参数选择是智能算法研究的难点，iACO模型也存在同样的问题。目前，文献中大多通过实验试探，得到算法的最优参数。但iACO用户评价值具有不确定性，用户偏好会调整改变，如何寻找鲁棒性的参数是值得研究的问题。

3 改进的交互式蚁群算法设计

3.1 交互式蚂蚁算法模型

文献[13]提出了一种交互式蚂蚁算法（interactive ant system，iAS）模型，并应用于成套服装（分为夹克、T恤、裤子和鞋子4部分）的选择。因为在该问题中没有启发式信息，所以第k只蚂蚁选择一套服装第i个部分的第 j个款式的概率和信息素更新公式分别如下[13]：

类似于遗传算法的处理，为保留全局历史最优解，该iAS模型使用精英保留策略，即用户选择的若干满意解（2至3个），直接保留到下一代。

3.2 改进的iACO模型

在文献[13]中，对问题的一般性描述和蚂蚁构筑解方式的介绍不够，本文将给予补充，并在此基础上给出相应的改进措施。

在iACO模型中，设潜在解为x=(x1,x2,…,xp),其中变量x（ii=1,2,…,p）有ni种取值。本文考虑一类无约束的隐性目标优化问题：

max f(x)

因为被优化系统目标函数与决策变量间的数量关系难以建立，所以利用人来评价问题解对应的系统输出，并将其评价值作为目标函数值。

将信息素直接放置在各决策变量上，把变量xij上的信息素水平记为τij(i=1,2,…,p，j=1,2,…,ni）。蚂蚁在第i维决策变量上选择第 j个取值的选择概率如下：

蚂蚁在参数空间中的行走路线如图1所示。

Fig.1 Trails of ants in pheromone space图1 蚂蚁在信息素空间中的行走路线

各点上的信息素初始值可设置为：

其中，τ0是初始信息素水平。

m只蚂蚁在一次迭代中构造m个解，为了提高算法搜索效率，每构造一个新解，要求其与之前所有代构造的所有解均不一样。然后将当前代构造的m-1个解与上一代用户选择的最好解一并输出，交给用户评价，以确定当前全局历史最优解Sgb，并进行信息素更新操作，更新公式如下：

其中,i=1,2,…,p,j=1,2,…,ni,ρ是信息素残留系数，Q是Sgb所在最优路径上的信息素增量。为了防止某些路径上的信息素过高或过低造成的蚂蚁过度偏向选择某些路径，将信息素限制在适当区间内，即：

3.3 用户评价方式

在IEC中，用户评价方式有全体评价和部分评价两种。全体评价就是要求用户评价每一代所有进化个体的适应值；部分评价只需要用户评价部分其感兴趣个体的具体适应值，而未评价个体的适应值则根据距离或代理模型等进行适应值估计。因此，IEC用户的评价任务是非常繁重的。

相比较而言，本文iACO用户的评价则简易许多，这主要是由iACO模型的特点决定的。因为模型中只根据迄今历史最优解Sgb进行信息素的更新，并且更新时不需要具体的用户评价值，所以用户不必评价每一代中进化个体的具体优劣值，而只要指出哪一个个体是迄今历史最优解Sgb就可以了。同时，在后面实际实验系统中，将上一代用户选择的Sgb放在界面的第一位，让用户方便和其他新构造的m－1个解进行比较。经过这样处理后，用户评价简单而又轻松，大大降低了用户的评价疲劳。

3.4 算法参数的讨论

对iACO模型，其中相关参数具有如下性质：

定理 iACO算法迭代到第n代时，任意一条路径上的信息素大小为：

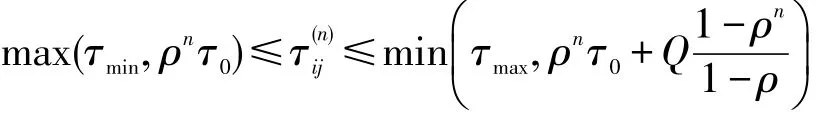
证明 先不考虑最大最小信息素约束，若信息素τij所在的路径(i,j)始终为最优路径，则由式（5）～（7）可知：

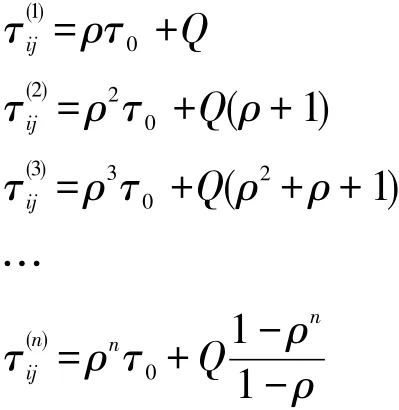
若信息素τij所在的路径(i,j)始终为非优路径，易知：

而一般路径(i,j)上的信息素在第n代时处于以上两种情况之间，同时又满足最大最小信息素的限制，从而可得定理结论。 □

证明 显然始终没有选中成为优化路径上的信息素最快取到最小信息素值，即有：

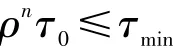
推论2若取τ0=τmax，则当Q≤(1-ρ)τmax时，最优路径上的信息素不会超过τmax。

证明 由假设知Q≤(1-ρ)τmax=(1-ρ)τ0从而有

即最优路径上的信息素不会超过τmax。 □

本文iACO模型一共涉及5个参数，以上定理和推论为设置算法参数提供了理论指导，同时通过多次实验获得优化参数。

对于初始信息素水平τ0，其值越大，则会在算法运行的初始若干代内保证各条路径上的信息素具有一个较高的水平，但随着信息素的挥发，其作用逐渐减弱。在式（6）中，其右边第1项与第2项分别表示信息素挥发和强化过程，参数ρ与Q的作用与传统ACO类似。

由推论1可知，残留系数ρ的取值不易过小，否则信息素挥发过快，非优路径上信息素会很快取到最小信息素值τmin。经过实验，残留系数ρ最优取值区间为[0.10,0.74]，实验中取ρ=0.50。

由推论2可知，当取τ0=τmax时，参数Q值越大，使得优化路径上信息素水平很快累积到最大信息素取值τmax，从而会弱化初始信息素水平τ0的作用，使算法易陷入局部优化。经过实验发现，τ0与Q配合起来设置较好，其优化值较容易获得，实验中取τ0= τmax=26,Q=1。

最小信息素水平τmin的取值不能过大，这样会使各路径上的信息素水平过于平均，不利于搜索。经过实验测试发现，τmin取值在区间[0.01,0.08]时，具有较好的综合性能。实验中，取τmin=0.022。

注意，以上定理和推论对参数设置具有一般性指导意义，其具体参数取值，是以4.1节函数优化实验得到的优化参数。实际上，在遇到不同类型或不同领域模型时，由于问题规模、全局最优解与局部最优解分布及参数空间形状等不同，搜索难度会不同，算法优化参数也会有所不同，需要根据实际问题进行测试以得到合适的参数。

3.5 算法步骤

iACO算法的具体实现过程如下：

步骤1初始化。设定算法参数,均匀放置初始信息素。

步骤2解的构建。先完成当前代一个解的构建：为保证一定的随机性，当生成的随机数rand＜P0（P0为一较小值）时，以随机方式构建直至找到一个与之前所有代解均不同的新解；否则(rand≥P0)，蚂蚁根据各条路径上的信息素水平，按选择概率公式（4）通过从图1所示的路径来完成一个解的构建（要求同前）。若是第一代，则一共构建m个解，输出到用户界面上；若代数大于1，则仅需要构建m－1个解，并与之前用户选择的全局历史最优解Sgb一起显示在用户界面上（Sgb的位置排在第一）。

步骤3用户评价。用户比较当前代解的优劣，重新确定迄今全局历史最优解Sgb。

步骤4终止判定。若满足终止条件，则输出结果，结束算法；否则按式（6）～（8）对信息素进行更新操作，转步骤2。

另外，在步骤2中设置算法停滞标志flag，即在构造当前解时，若与之前所构造的解重复5 000次，则认定算法陷入停滞，提前终止算法，并输出相关提示。实验中，P0取0.05。

4 仿真实验

4.1 函数优化实验

为了获得客观的比较结果,利用无约束的函数优化实验来模拟iACO模型的求解过程，即将iACO用户评价改为函数计算，本文用以下测试函数进行模拟实验。

为了说明方便，将文献[13]和文献[15]中两类交互式蚂蚁算法分别记为iAS1和iAS2。对以上函数实验数据，分别使用标准遗传算法GA、iAS1、iAS2和iACO算法进行求解，得到在不同种群规模情况下的优化结果如表1所示。在表1中，每个算法独立执行10 000次并统计结果；3类算法最大迭代代数均设定为100；iAS1和iACO算法在构造新解时，记录与之前构造解的重复次数，若重复次数达到5 000次，则判定算法陷入停滞，算法寻优失败；GA、iAS1和iACO算法均采用精英保留策略。iAS2对陷入停滞有相应的处理方法，其进化采用文献[15]的方式，为了比较的合理性，在统计信息时每一代以采用精英保留策略的种群作为统计对象。GA的交叉概率取0.8,变异概率取0.07；iAS1算法每一代选择3个最好解保留到下一代。

Table 1 Results of 4 algorithms for function optimization表1 4类算法对函数的优化结果

从表1中可以看出，在不同种群规模情况下，GA搜索平均收敛代数接近60代，搜索到最优解的成功率在52%以内，性能较低。iAS1算法收敛代数令人满意，但成功率偏低，整体性能较低。iAS2算法在种群规模12以上时，成功率接近或达到100%，收敛代数较iAS1算法偏大。本文的改进算法iACO在10 000次搜索均找到最优解，成功率为100%；在使用相同规模的种群情况下，其收敛代数介于iAS1和iAS2算法之间，在20代左右，综合性能表现良好。

为了进一步了解以上4类算法的进化收敛情况，分别运行算法统计每代的最好解适应值和种群平均适应值，得到结果分别如图2和图3所示。由图可以看出，3类蚁群算法的收敛速度均比GA快，适合精细化搜索；GA算法运行代数长，收敛慢，性能偏低；iAS1算法表现出较好的收敛性能，但由表1知该算法易陷入停滞；iACO则表现出较好的综合性能。

为了测试以上4类算法对一般函数的优化性能，下面使用文献[16]的基于网格划分策略的连续域蚁群优化方法进行测试，并将文献[16]中的蚁群优化策略分别改为本文的iAS1、iAS2和iACO算法的优化策略即可。所测试的函数优化问题如下：

Fig.2 Evolution of the best fitness value of 4 algorithms to optimizef1function图2 4类算法优化 f1函数时最好解进化情况

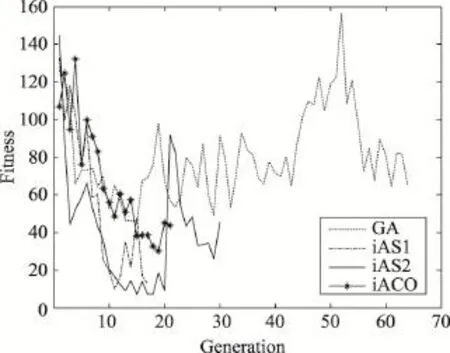
Fig.3 Evolution of average fitness value of 4 algorithms to optimizef1function图3 4类算法优化 f1函数时平均适应值进化情况

例2 min f2(X)=-[x1sin(9πx2)-x2cos(25πx1)+20]，其中x1,x2∈[-10,10]。

例4 min f4(X)=-[21.5+x1sin(4πx1)+x2sin(20πx2)，其中x1∈[-3.0,12.1],x2∈[4.1,5.8]。

在优化时涉及到的蚂蚁数目等算法参数请参考文献[16]的设置，其余涉及本文算法的参数使用本文设置。其中有变动的参数包括：GA的交叉与变异概率分别取0.9和1/Li，Li表示函数 fi(i=2,3,4)中个体的二进制编码长度，GA种群规模取30，进化最大代数为1 000代；函数 f2的等分数N=33。记录4类算法分别优化以上3个函数时每代最好解，并将前300代的结果分别展示在图4～图6中。鉴于300代以后的优化结果在图中基本是重叠的，故未画出。

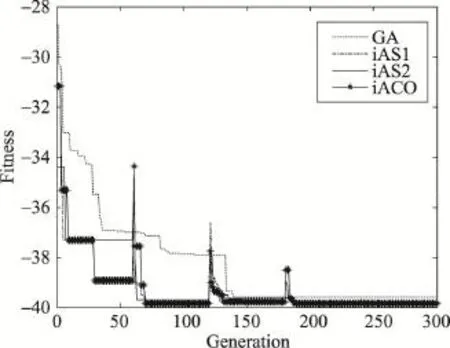
Fig.4 Evolution of the best fitness value of 4 algorithms to optimizef2function图4 4类算法优化 f2函数时最好解进化情况

Fig.5 Evolution of the best fitness value of 4 algorithms to optimizef3function图5 4类算法优化 f3函数时最好解进化情况

Fig.6 Evolution of the best fitness value of 4 algorithms to optimizef4function图6 4类算法优化 f4函数时最好解进化情况

由于文献[16]的求解思想是先在参数空间内打网格，使用ACO算法求解当前的最好解；然后以当前最好解为中心进行网格划分，再使用ACO算法求解，如此往复直到求解到合适的精度停止。每做一次网格划分，即为一个周期；并且随着周期的增长，变量x的取值范围会越来越小，因此iAS1、iAS2和iACO算法统计的当前代最好解在图中表现出阶跃性和周期性。

从图4～图6中可以看出，GA在优化函数 f4时，初始收敛性能好于其他3类算法，但在中后期收敛性能不及iACO算法。iACO算法在优化函数f2和 f3时的收敛性能要好于GA、iAS1和iAS2算法，综合优化性能最优。

4.2 汽车造型设计实验

为验证算法的实用性和运行性能，使用汽车造型设计系统[4,15]进行测试。iACO的系统进化界面如图7所示。其中，用户若在上一代选择了nb个满意解，则在进化界面上的前nb个系统输出即为其上一代选择的满意解，本文算法nb=1；文献[13]算法使用精英保留策略，nb=3。

Fig.7 System interface of iACO图7 iACO系统进化界面

3类算法分别独立运行10次进行比较，结果如表2所示。其中，3类算法的种群规模均取12，最大进化代数为30代，其他参数设置同4.1节。标准iGA算法的平均比较次数中，每一代中的相同个体不记入评价次数。

Table 2 Results of 3 algorithms for car styling design表2 3类算法对汽车造型设计的优化结果

从表2中可以看出，iGA用户平均评价次数约230次，远高于其他3类算法；iGA的平均收敛代数比iAS1和iACO算法高出近10代，比iAS2算法也要高出近6代。同时，iGA用户必需给出每一个个体的具体适应值，因此用户评价的负担是非常繁重的，故iGA的整体性能低。iAS1与iACO算法平均进化代数相近，但iAS1用户要求每一代选定3个最为满意的解，因此其评价次数要比iACO多出近2.8倍；由于iAS2算法要比较全局历史最优解、当前代最优解和上一次信息素重新初始化后的最优解之间的优劣，故其用户评价次数与iAS1算法相近。总体来看，基于蚁群搜索的iAS1、iAS2与iACO用户每一代只需要选择其满意的1至3个解，而不必给出选定解的具体评价值，因此操作简单而又轻松，极大地降低了用户疲劳。不难看出，4类算法中iACO具有最好的运行性能。

需要指出的是，和传统智能算法一样，本文算法也会有陷入局部优化的可能，若陷入局部优化，则判定算法寻优失败，需要重新运行算法。

5 结束语

本文深入分析了iACO模型的研究难点，并讨论解决思路。针对Tanabe等人提出的交互式蚂蚁算法模型的不足，提出了一个改进iACO模型，给出其求解问题的一般性描述、蚂蚁构造解的方式、转移概率的计算与信息素的更新方法；模型运用全局历史最优解进行信息素更新，并将信息素限定在适当区间内；对模型参数进行了理论分析；从人机交互的特点出发，设计了合理的用户评价策略；最后，利用函数优化和汽车造型设计进行了实验比较，结果表明本文算法具有较高的运行性能，有着良好的应用前景。

iACO算法进一步研究的问题有：提高算法的性能；用户疲劳问题处理；将算法应用到其他相关实践领域。

[1]Marco D,Thomas S.Ant colony optimization[M].Cambridge,USA:MIT Press,2004.

[2]Xu Yongcheng,Chen Ling.Community detection on bipartite networks based on ant colony optimization[J].Journal of Frontiers of Computer Science and Technology,2014,8 (3):296-304.

[3]Chen Guangpeng,Yang Yubin.Memory-type image retrieval method based on ant colony algorithm[J].Journal of Frontiers of Computer Science and Technology,2011,5(1):32-37.

[4]Meng Weidong,Huang Yongqing,Lu Qing,et al.Adaptive interactive genetic algorithm oriented to car styling design[J]. Computer Engineering and Applications,2012,48(21):240-243.

[5]Simons C L,Parmee I C.Elegant,object-oriented software design via interactive evolutionary computation[J].IEEE Transactions on Systems,Man,and Cybernetics:Part C, 2012,42(6):1779-1805.

[6]Yang Yanpu,Liu Qiong.Product form design method driven by design intent[J].Computer Integrated Manufacturing Systems,2015,21(4):867-874.

[7]Sun Xiaoyan,Lu Yina,Gong Dunwei,et al.Interactive genetic algorithm with CP-nets preference surrogate and application in personalized search[J].Control and Decision, 2015,30(7):1153-1161.

[8]Dou Runliang,Zong Chao,Nan Guofang.Multi-stage interactive genetic algorithm for collaborative product customization[J].Knowledge-Based Systems,2016,92:43-54.

[9]Gong Dunwei,Chen Jian,Sun Xiaoyan.Novel interactive genetic algorithm for estimating individual fitness based on similarity[J].Control Theory&Applications,2013,30(5): 558-566.

[10]Gong Dunwei,Guo Guangsong,Lu Li,et al.Adaptive inter-active genetic algorithms with interval fitness of evolutionary individuals[J].Progress in Natural Science,2008,18(3): 359-365.

[11]Sun Xiaoyan,Chen Shanshan,Gong Dunwei,et al.Weighted multi-output Gaussian process-based surrogate of interactive genetic algorithm with individuals interval fitness[J]. ActaAutomatica Sinica,2014,40(2):172-184.

[12]Sun Xiaoyan,Gong Dunwei,Jin Yaochu,et al.A new surrogate-assisted interactive genetic algorithm with weighted semisupervised learning[J].IEEE Transactions on Cybernetics, 2013,43(2):685-698.

[13]Tanabe R,Gonsalves T,Itoh K.Interactive ACO algorithm toward practical IEC application fields[C]//Advanced Methods,Techniques,and Applications in Modeling and Simulation:Proceedings in Information and Communications Technology,2011 Asia Simulation Conference,Seoul,Nov 2011:308-315.

[14]Simons C L,Smith J,White P.Interactive ant colony optimization(iACO)for early liftcycle software design[J]. Swarm Intelligence,2014,8(2):139-157.

[15]Huang Yongqing,Zhang Xiangde,Li Xudong.Interacitve ant system[J].Control and Decision,2012,27(4):609-612.

[16]Huang Yongqing,Hao Guosheng,Zhong Zhishui,et al.Improved ant colony algorithm based on grid strategy for continuous space optimization[J].Computer Engineering and Applications,2013,49(9):61-64.

附中文参考文献：

[2]徐永成,陈崚.基于蚁群优化的二分网络社区挖掘[J].计算机科学与探索,2014,8(3):296-304.

[3]陈光鹏,杨育彬.利用蚁群算法的记忆式图像检索方法[J].计算机科学与探索,2011,5(1):32-37.

[4]孟伟东,黄永青,陆青,等.面向汽车造型设计的自适应交互式遗传算法[J].计算机工程与应用,2012,48(21):240-243.

[6]杨延璞,刘琼.设计意图驱动的产品形态设计方法[J].计算机集成制造系统,2015,21(4):867-874.

[7]孙晓燕,陆宜娜,巩敦卫,等.基于CP-nets的偏好感知交互式遗传算法及其个性化搜索[J].控制与决策,2015,30 (7):1153-1161.

[9]巩敦卫,陈健,孙晓燕.新的基于相似度估计个体适应值的交互式遗传算法[J].控制理论与应用,2013,30(5):558-566.

[11]孙晓燕,陈姗姗,巩敦卫,等.基于区间适应值交互式遗传算法的加权多输出高斯过程代理模型[J].自动化学报, 2014,40(2):172-184.

[15]黄永青,张祥德,李旭东.交互式蚂蚁算法[J].控制与决策,2012,27(4):609-612.

[16]黄永青,郝国生,钟志水,等.基于网格划分策略的连续域改进蚁群算法[J].计算机工程与应用,2013,49(9):61-64.

HUANG Yongqing was born in 1974.He received the Ph.D.degree in management science and engineering from Hefei University of Technology in 2007.Now he is a professor at Tongling University.His research interests include evolutionary computing and ant colony optimization,etc.

黄永青（1974—），男，湖北黄梅人，2007年于合肥工业大学管理科学与工程专业获得博士学位，合肥工业大学博士后，现为铜陵学院计算机系教授，主要研究领域为进化计算,蚁群优化等。

YANG Shanlin was born in 1948.He is an academician of China Academy of Engineering,and professor and Ph.D.supervisor at Hefei University of Technology.His research interests include decision science and technology, data mining and artificial intelligence,etc.

杨善林（1948—），男，安徽安庆人，中国工程院院士，合肥工业大学教授、博士生导师，主要研究领域为决策科学与技术，数据挖掘，人工智能等。

LIANG Changyong was born in 1965.He is a professor and Ph.D.supervisor at Hefei University of Technology. His research interests include decision analysis,data mining and artificial intelligence,etc.

梁昌勇（1965—），男，安徽肥西人，博士，合肥工业大学教授、博士生导师，主要研究领域为决策分析，数据挖掘，人工智能等。

Improved InteractiveAnt ColonyAlgorithm and ItsApplication*

HUANG Yongqing1,2+,YANG Shanlin1,LIANG Changyong1
1.School of Management,Hefei University of Technology,Hefei 230009,China
2.Institute of Information Technology and Engineering Management,Tongling University,Tongling,Anhui 244000,China
+Corresponding author:E-mail:yongqinghuangbs@sina.com

Interactive ant colony optimization(iACO)is a technique that optimizes target systems based on human evaluation.It can be used to solve the systems whose optimization indices are unable or difficult to be quantificated. Firstly,this paper analyzes the difficulties faced by iACO model.Nextly,aiming at the low performance of interactive ant system that is put forward by Tanabe et al.,this paper proposes an improved iACO algorithm.The pheromone in the proposed model is updated with the best ant and limited to a certain range.The method of constructing solutions and evaluating strategies from the perspective of human-computer interaction are discussed.Finally,the results of the experiments of function optimization and car styling draft design show that the proposed algorithm has higher optimization performance.

10.3778/j.issn.1673-9418.1509093

A

TP18

*The National Natural Science Foundation of China under Grant Nos.71271072,71331002(国家自然科学基金);the Postdoctoral Science Foundation of China under Grant No.2014M560508(中国博士后科学基金);the Fundamental Research Funds for the Central Universities of China under Grant No.2013HGBH0029(中央高校基本科研业务费专项资金);the Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No.20110111110006(高等学校博士学科点专项科研基金);the Natural Science Foundation of Anhui Province under Grant No.1208085MG121(安徽省自然科学基金);the Research Foundation of Educational Commission ofAnhui Province under Grant Nos.KJ2012A269,SK2015A537(安徽省教育厅重点项目);the Scientific Research Foundation of Tongling University under Grant No.2014tlxyxs31(铜陵学院科研项目).

Received 2015-09,Accepted 2016-01.

CNKI网络优先出版:2016-01-04,http://www.cnki.net/kcms/detail/11.5602.TP.20160104.0953.002.html

Key words:interactive ant colony optimization;ant colony optimization;human-computer interaction;car styling