太阳影子定位的数学模型构建
王 丹,刘 凯,闫 东,李 新
(1.吉林建筑大学城建学院 基础部;2.吉林建筑大学城建学院 管理工程系,吉林 长春 130114)
太阳影子定位的数学模型构建
王 丹1,刘 凯2,闫 东2,李 新2
(1.吉林建筑大学城建学院 基础部;2.吉林建筑大学城建学院 管理工程系,吉林 长春 130114)
根据直杆在太阳下影子的长度及方位角,建立视频拍摄地点和日期的最小二乘法模型,利用PREWITT算子对直杆顶部进行边缘检测求得直杆影子的顶点坐标,运用MATLAB求解,从而得到视频拍摄地的经纬度和日期.
最小二乘法;MATLAB;边缘检测算法
1 问题的提出及假设
在当今数码科技高速发展的时代,对视频数据分析已成为一项重要的研究课题,在反恐及刑事侦查等方面有着重要应用.本文通过对视频中物体影子在不同地点、不同日期和不同时间长度和角度的变化规律的分析建立数学模型,确定视频拍摄的地点和日期.问题数据来自于2015年全国大学生数学建模竞赛A题[1].
根据模型简化求解的需求,本文提出以下假设:
⑴假设地球南北极对称;
⑵假设杆竖直向上;
⑶假设附件提供的数据全部准确可靠.
2 太阳影子长度的数学模型
太阳影子长度与赤纬角、时角及太阳高度角等因素有关.
一年中第d天,太阳直射地球的纬度(即赤纬角)如图2所示
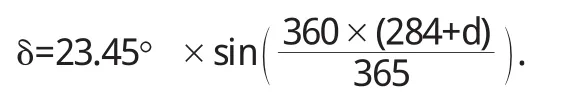
对于任意时刻t0,对应的时角为

某地太阳光线与该地作垂直于地心的地表切线的夹角θ(称为太阳高度角)可以通过如下公式求得:

以直杆及其太阳影子为两直角边,太阳高度角为一角可构造一个直角三角形,根据三角函数可得如下关系式:
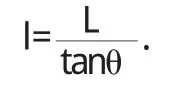
l为影子长度;L为已知直杆杆长.
公式⑴中所用时间为钟表时间,即平太阳时,指的是地球绕太阳的旋转轨迹是标准的圆形.若考虑地球绕太阳的轨迹为椭圆,地球对太阳的自转不是均匀的,得到的时间为真太阳时.因此,在公式⑴中应考虑真平太阳时差(Wb为经度差).
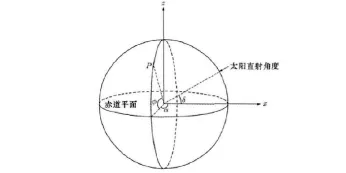
图1 太阳照射地球示意图
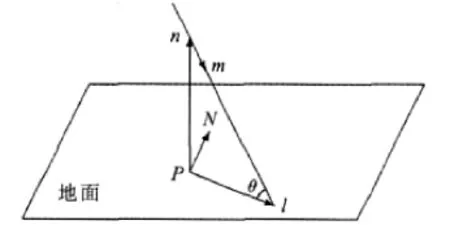
图2 太阳高度角示意图
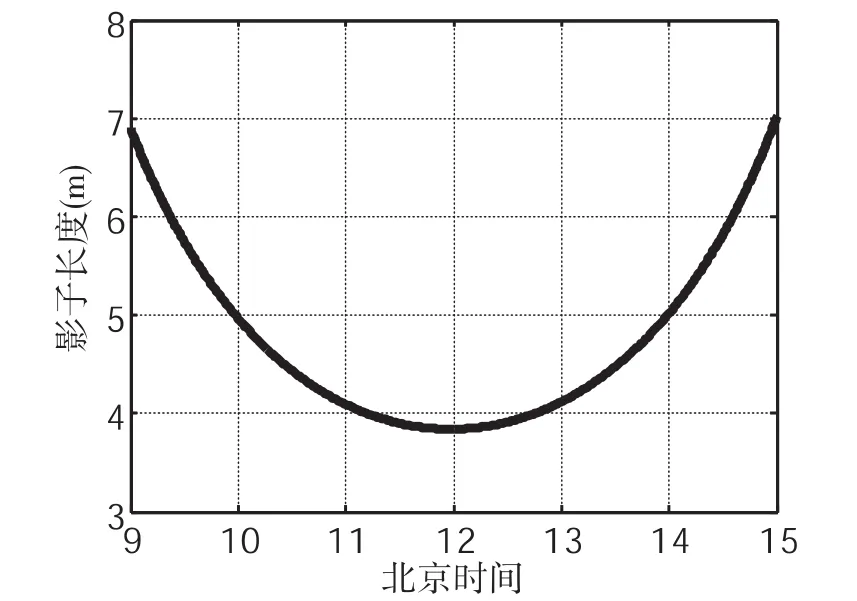
图3 太阳影子长度的变化曲线
利用MATLAB软件求解上述模型[2],得出2015年10月22日北京时间9:00-15:00之间,天安门广场3m高的直杆的太阳影子长度的变化曲线如图3所示:
3 确定地点的模型
记l(t0)为t0时刻直杆影子的理论长度,则
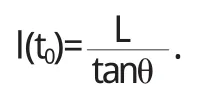
其中,θ为t0时刻的太阳高度角,计算公式为:

记lR(t0)为t0时刻直杆影子的实际测量出的长度:
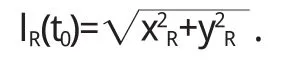
其中,(x2R,y2R)为t0时刻测量直杆影子端点坐标的测量值.
根据最小二乘法构建模型

考虑约束条件:

通过附件1所给数据,利用MATLAB计算得到经纬度[4],并利用绝对误差分析影长的误差,绝对误差公式如下:

计算所得误差结果如表1所示.
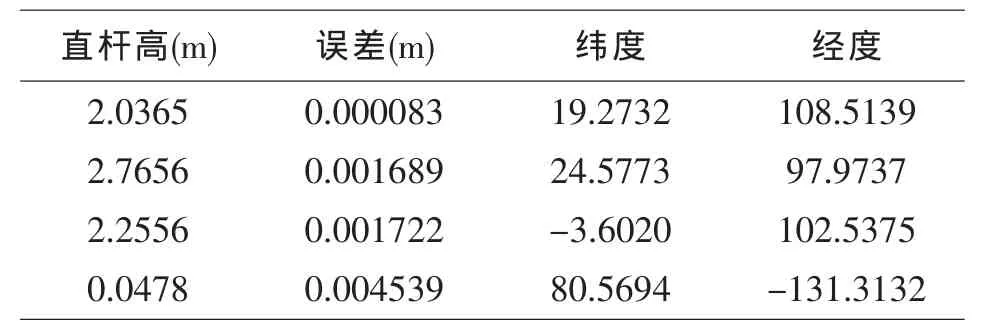
表1 经纬度及误差计算结果
根据计算结果,可确定所有可能的拍摄地点为海南、云南德宏傣族景颇族自治州、印度尼西亚和加拿大.
4 视频数据确定地点的模型

图4 不同时刻影子顶点坐标
利用'prewitt'算子进行边缘检测,得出直杆影子顶点的位置,测得不同时刻影子顶点的坐标,如图4所示.
由函数

其中2为杆长,905为杆顶端的像素坐标,226为原点像素坐标,X,Y为影子顶点像素坐标值.可计算出杆影子顶点准确坐标.
采用3中模型⑵⑶⑷
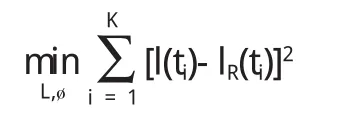
且满足约束条件
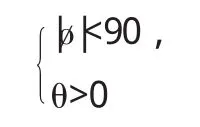
利用MATLAB计算得到经纬度,并利用绝对误差分析影长的误差,绝对误差公式如下:
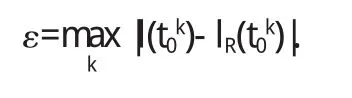
计算所得误差结果如表2所示:

表2 视频经纬度及误差计算结果
由计算结果可知视频拍摄地点为山西大同或印度尼西亚.
5 模型的应用
本文建立的太阳影子定位模型,给出了不同日期、不同时间以及不同影长条件下如何确定地点(经纬度)的算法,对解决无测量工具并处在手机信号较差的偏远山区无法确定方向的问题有较大的帮助.
〔1〕2015年高教杯全国大学生数学建模竞赛A题.http:// www.mcm.edu.cn.
〔2〕Akram Abdulameer Abood,A comprehensive solar angles simulation and calculation using matlab,INTERNATIONALJOURNALOFENERGYANDENVIRONMENT,Volume 6,Issue4,2015 pp.367-376.
〔3〕邱国全.太阳时的计算[J].太阳能,1998(01):7.
〔4〕王志新.MATLAB程序设计及其数学建模应用[M].北京:科学出版社,2013(6):34-37.
〔5〕司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2012(5):318-324.
P128
A
1673-260X(2016)11-0008-02
2016-08-12

