300M钢耳片孔挤压强化全过程有限元模拟
何志明, 张晓晶, 刘天琦, 杨树勋
(1.上海交通大学 航空航天学院,上海 200240;2.中航工业北京航空材料研究院,北京 100095)
300M钢耳片孔挤压强化全过程有限元模拟
何志明1, 张晓晶1, 刘天琦2, 杨树勋1
(1.上海交通大学 航空航天学院,上海 200240;2.中航工业北京航空材料研究院,北京 100095)
采用三维非线性有限元方法模拟300M钢耳片开缝衬套冷挤压的完整过程.分析开缝衬套挤压、铰孔及孔边挤压三道工序对孔边残余应力场的影响,与试验测量结果进行比较,表明模拟过程是可行、有效的.开展铰削量及孔边挤压预制倒圆角半径的参数化分析,给出铰削量对残余应力场的影响规律及最佳的预制倒圆角半径,通过疲劳试验及断口分析验证模拟结果的合理性.疲劳试验结果表明,经过开缝衬套挤压及铰孔工艺之后,疲劳寿命提高近137%,进行孔边挤压强化会将疲劳寿命提高183%.
孔挤压;残余应力;有限元模拟;疲劳寿命
在现代航空工业中,孔挤压工艺被广泛用于提高带孔飞行元件的疲劳寿命,带孔元件会产生应力集中,容易产生疲劳裂纹[1-2].孔挤压强化工艺是指用具有一定过盈量的挤压棒连续、均匀地挤压孔,使孔周围产生一个弹塑性变形层,即残余压应力层[3].孔挤压产生的残余压应力会显著降低疲劳过程中外界交变载荷的平均应力,从而提高疲劳寿命,这已经被许多研究所证实[4-7].孔挤压过程主要包括挤压孔内壁和铰孔两道工序,为了防止孔边出现裂纹,可以进行孔边挤压.
针对孔挤压残余应力场的模拟,国内外不少学者都进行了相关的研究.Nigrelli等[4]采用完整模型模拟开缝衬套挤压过程,考虑衬套开缝位置以及板厚对残余应力场的影响.Karabin等[8]采用三维模型模拟材料在不同厚度上性能变化对孔挤压塑性应变的影响,并且利用二维模型模拟新的衬套开口形状对塑性应变的影响.刘晓龙等[9]使用ANSYS模拟7050-T7451板的三维孔挤压过程,研究板厚对残余应力场的影响.欧阳小穗等[10]采用Marc模拟7075铝合金板开缝衬套挤压和芯棒挤压的残余应力场,并进行后续的寿命预测.Yuan等[11]采用ABAQUS模拟TC4板开缝衬套挤压过程,分析摩擦系数对残余应力场的影响,进行多轴应力状态下的疲劳寿命预测.Mahendra等[12]采用新的简化模拟方法,能够模拟残余应力沿板厚方向的变化,避免了接触分析所需要花费的巨大资源.Liu等[13]采用芯棒加载及孔边位移加载的方式模拟孔挤压过程,比较挤压量、摩擦系数及两种加载方式对残余应力场的影响,通过疲劳试验及SEM断口分析比较不同挤压量下LY12-CZ的疲劳增益效果和裂纹起源位置.以上模型均能够有效模拟孔挤压过程产生的残余应力场,但忽视了孔内壁挤压之后的铰孔过程.另外,由于孔边挤压的引入,残余应力场会发生进一步变化,因此,需要作进一步的探讨.
本文采用ABAQUS有限元分析软件模拟300M钢耳片孔挤压的完整过程,包括开缝衬套挤压、铰孔和孔边挤压,所得的残余应力场与试验结果吻合较好.通过参数分析模拟铰削量及预制倒圆角半径对孔边残余应力的影响,给出铰削量对残余应力场的影响规律,确定最佳的预制倒圆角半径,通过疲劳试验给出孔边挤压对疲劳寿命的增益效果.
1 有限元模型
孔挤压工艺过程的顺序如下:首先为开缝衬套挤压,其次是铰孔及倒圆过程,最后是孔边挤压的过程.模拟时,先进行单纯的开缝衬套挤压过程模拟,确定挤压后孔径初始变形量,根据终孔直径确定后续铰孔及倒圆过程中需要去掉的材料量.经过这个过程,可以提前规划好需要铰削的位置,分别将铰削部分和未铰削的基体进行单元划分,保证后续残余应力场的叠加和孔边挤压过程有相对独立的单元.重新完成孔挤压全过程的有限元模拟,即开缝衬套挤压、铰孔和孔边挤压.
耳片的几何尺寸如图1所示,材料为300M钢,有限元模型取试样的1/4,耳片初孔直径为19.75 mm,终孔直径为20 mm,挤压量为0.8%~1%.采用FTI衬套,材料为不锈钢1Cr17Ni7,厚度为0.457 mm.芯棒采用V2合金钢,工作段直径为19.016 mm,可由挤压量推算出来.模拟时衬套开缝处朝耳片的加载方向(见图2(b)),防止在孔边应力集中最严重处造成损伤.
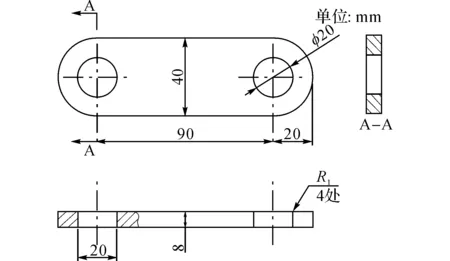
图1 耳片的几何尺寸Fig.1 Geometry of 300M steel lug

图2 开缝衬套挤压有限元模型Fig.2 FEM model of split-sleeve expansion
采用ABAQUS有限元软件对耳片、芯棒和衬套进行有限元建模.开缝衬套挤压的有限元模型如图2所示,耳片和衬套均采用8节点六面体减缩积分单元(C3D8R),其中耳片单元数为185 700(在远离孔边的地方网格划分较粗,粗细网格邻接区采用ABAQUS中的Tie约束绑定在一起,避免单元数过大同时保证孔边单元数量足够),衬套单元数为12 350,芯棒采用离散刚体进行模拟.耳片孔边单元尺寸最小,为0.100 mm×0.517 mm×0.160 mm.在衬套开缝处,网格加密,尺寸为0.100 mm×0.104 mm×0.160 mm.
假设开缝衬套为线弹性,耳片为弹塑性材料,屈服强度为1 695 MPa.耳片与衬套、衬套与芯棒之间通过接触相互作用,各部件类型及材料属性如表1所示.表中,E为弹性模量,μ为泊松比.

表1 各部件定义及材料属性
使用弹塑性本构关系描述300M钢耳片在孔挤压过程中的响应,有限元模型中采用的300M钢的真实应力σ-应变ε曲线如图3所示.

图3 300M钢真实应力-应变关系Fig.3 300M steel true stress-strain curve
分析孔挤压的实际约束情况,图2(a)中模型左边界施加Y方向对称约束,模型右前边界约束X方向位移,在模型挤出面的节点(内径为25.75 mm和外径为35.75 mm的垫片内的节点)上约束Z方向位移.如图2(b)所示为模型局部示意图,给出挤入端、中部、挤出端及衬套开缝处位置(衬套开缝处经过倒圆角处理,防止出现耳片变形过大导致模型不收敛的情况).芯棒约束为刚体,通过控制芯棒的Z向位移来实现孔挤压的过程,Z向位移由0 mm变为-20 mm,即表示芯棒由工件的挤入端挤入,从挤出端挤出.

图4 铰削部分及孔边挤压模型Fig.4 Reaming part and model of hole edge expansion
经过开缝衬套挤压,耳片孔边径向平均位移约为0.025 mm,耳片孔径由19.75 mm增大到19.80 mm(取挤入端、中部和挤出端平均值),因此需要沿径向铰削0.1 mm才能达到终孔直径20 mm.由此可以确定铰削部分的几何尺寸,如图4(a)所示.将铰削部分作为一个单独部件与耳片基体通过Tie约束连接在一起.重新进行开缝挤压过程,此时,耳片单元数略有变化,耳片基体为177 072个单元,耳片铰削及倒圆角去除部分为6 596个单元.之后通过单元删除模拟铰削部分材料约束的释放.如图4(b)所示为孔边挤压模型.模拟时,通过上下倒角器的移动对耳片孔边进行挤压,挤压力主要来自设计倒圆角与预制倒圆角半径之差.本文中耳片设计倒圆角半径1 mm,预制倒圆角半径0.9 mm.耳片边界条件与开缝衬套挤压过程基本一致,在孔边挤压之前,将铰孔之后得到的残余应力场赋给耳片基体,然后进行孔边挤压的过程.
以上的有限元过程涉及到材料非线性及几何非线性,同时需要考虑接触问题,耗时长,收敛困难,需要消耗较大的资源.需要注意的地方如下.1)接触分析过程的要求比较苛刻,需要准确的主从面关系,主面刚度较大,单元可以划分较粗,从面刚度较小,单元划分相对较细.2)要求选取合适的初始增量步,过大则会导致接触过程难以顺利建立,分析过程难以完成,过小则会需要消耗过大的计算量.
2 模拟结果及与试验结果对比
由于孔边周向应力对疲劳裂纹的扩展至关重要[14-15],只给出周向残余应力s结果.所给结果除特殊说明外,均选取危险截面(图1中A-A截面)上应力:1)残余应力随距孔边距离d1的变化趋势均以图5的虚线路径为起点,往材料内部延伸,挤入端、中部及挤出端即为耳片基体的上表面、中间厚度和下表面;2)表面残余应力随距挤入端距离d2的变化趋势所取路径为图5的虚线路径.
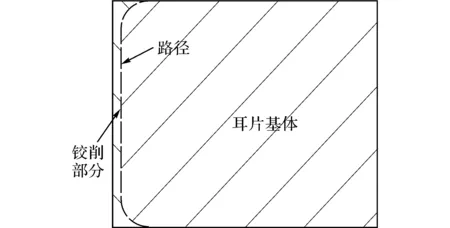
图5 危险截面示意图Fig.5 Diagram of dangerous section
2.1 铰孔前、后残余应力对比
开缝衬套挤压之后会进行一个铰孔(含预制倒圆角)过程,在耳片最危险截面,残余应力s随d1及d2的变化规律如图6所示.

图6 铰孔前、后的残余应力变化Fig.6 Residual stress variation before and after reaming
由模拟结果可知,开缝衬套挤压后,周向残余应力在挤出端最大,其中中部表面残余压应力最小.铰孔会对残余应力分布产生一定的影响,但影响很小.1)在相同物理位置,总趋势为残余压应力增大.2)铰孔之后新的孔表面与铰孔之前旧的孔表面的残余应力变化在2.4节给出.由于在靠近孔边的位置,残余压应力较大,铰孔去除一部分带残余压应力的材料,导致耳片后续部分的残余应力重新分布.由内力平衡可知,在同一位置铰孔之后残余压应力应增大,模拟结果合理.
2.2 孔边挤压前、后残余应力变化
孔边挤压会对孔的上、下边缘(即孔的挤入端和挤出端)残余应力产生较大的影响,模拟时比较了孔边挤压前、后残余应力随距挤入端距离的变化规律,由于变化不大,趋势与图6(b)类似,这里不再给出.如图7所示为耳片危险截面挤入、挤出端在孔边挤压前、后的应力分布.由于倒圆的存在,耳片危险截面挤入、挤出端几何形状为一个1/4圆.

图7 孔边挤压前后挤入、挤出端残余应力变化Fig.7 Residual stress variation in entrance and exit face before and after hole edge expansion
模拟结果表明,孔边挤压过程对孔的表面残余应力影响不大,但是在孔边(即挤入、挤出端),会明显改变残余应力分布.在挤入端,最大残余压应力增大,增幅约为120 MPa,同时位置由表面移到耳片内部,应力梯度增大;在挤出端,最大残余压应力略有增大,高压应力区域(-1 142~-944.5 MPa)明显增大,后续应力梯度也有一定程度的提高.
2.3 模拟结果与试验结果对比
残余应力的测量采用X射线衍射技术,设备为高功率X射线残余应力分析仪.测试时采用Cr靶,衍射晶面为(211),光斑间距为0.1 mm,所测位置位于图1的危险截面.沿深度方向应力分布测定采用剥层法.图8(a)给出未经过任何强化工艺的耳片表层残余应力场,说明原始的机械加工会在耳片表层产生残余应力.由拟合公式可以看出,在孔边残余压应力较大,随着距孔边距离的增大,表层残余应力呈现一个无规律的波动变化.经过完整的孔挤压过程的耳片残余应力场的试验结果如图8(b)所示,试验所测数据为挤入端残余应力与中部残余应力的平均值.
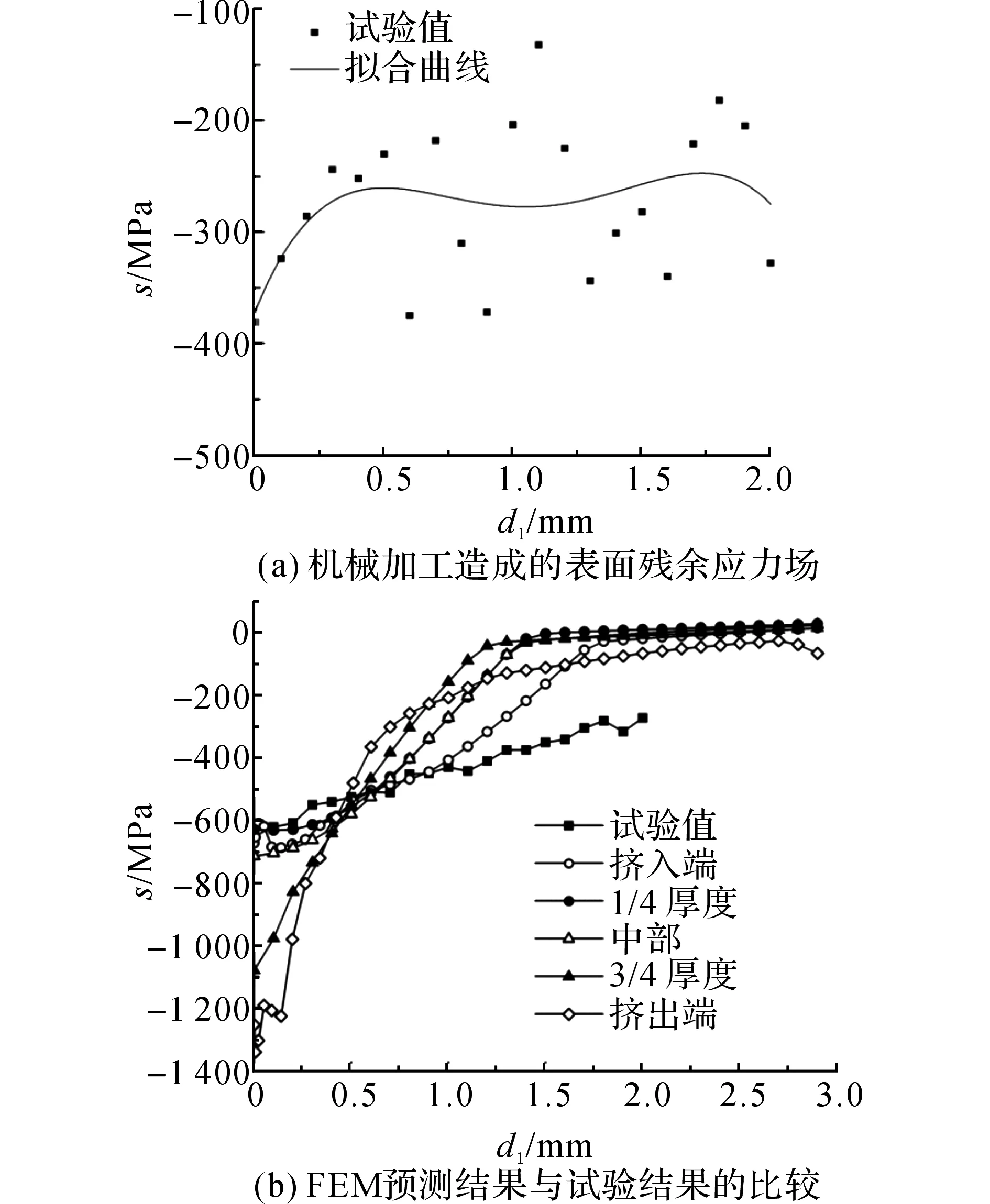
图8 残余应力测试结果与FEM预测结果的比较Fig.8 Residual stress comparison between experimental results and FEM results
由对比结果可以看出,在靠近孔边时,模拟结果与试验结果吻合较好,尤其是1/4厚度处的结果.当深度较深时,通过试验测得的残余压应力较模拟结果偏大,原因主要如下.1)机械加工过程在材料表层产生的残余应力难以模拟,原始的试验结果表明材料表面存在较大的机械加工残余压应力,即使在距孔边距离较大的地方,残余压应力为100~200 MPa.2)残余应力的测量采用逐渐剥层的方法进行,随着测量深度的增加,去掉含残余压应力的材料越来越多,残余应力重新分布,残余压应力及压应力区深度均有一定程度的提高,后续的模拟结果能够说明该趋势.3)在模拟过程中采用一些简化方法,如芯棒简化为刚体,衬套为弹性体,均可能产生一定的误差.
2.4 铰削量对残余应力场的影响
经过开缝衬套挤压之后,由于塑性变形的存在,孔的半径会增大,工艺上通常通过进一步的铰孔将孔的半径增大到最终的设计半径.由于本文中铰削量很小,残余应力场的变化也很小,可以假设残余应力场的变化与铰削量是相关的.通过参数分析的方法,模拟在开缝衬套挤压基础上的铰孔过程.铰削量Δ为半径方向的去除量,模拟Δ从0 mm增大到1 mm过程中残余应力场的变化.在考虑铰削量的变化过程中,不考虑耳片倒圆的影响.
模拟结果如图9所示.如图9(a)所示为挤入端残余应力随距孔边距离的变化趋势,距孔边距离为0 mm表示未铰孔时的孔表面,选择挤入端是因为挤入端残余压应力较小,裂纹容易从该处萌生.如图9(b)所示为残余应力随距挤入端距离的变化规律.

图9 铰削量对残余应力的影响Fig.9 Effect of reaming cuttings weight on residual stress field
模拟结果表明,铰削量越大,在相同的物理位置,残余压应力增大越明显,同理残余压应力的深度相应增大;随着铰削量的增大,材料表面残余压应力逐渐减小,其中挤出端变化最明显,主要是因为铰削过程将表层大的残余压应力区去除了.由此可以对工艺过程提出一定的改进建议,在孔挤压的过程中,铰削量只能作为一道工序来提高材料的表面质量,铰削量过大将会显著降低材料表面的残余压应力,大大降低孔挤压的强化效果,因此铰削量应尽可能小.
2.5 预制倒圆角半径对残余应力场的影响

图10 孔边挤压示意图Fig.10 Diagram of hole edge expansion
在孔边挤压过程中,设计倒圆角与预制倒圆角半径之差(以下简称半径差)是形成孔边挤压效果的主要原因,示意图如图10所示.孔边挤压时,外载作用于倒角器上端,倒角器向下移动,耳片孔边发生变形,耳片孔边倒圆角半径被压制成与倒角器孔边倒圆角半径一致,最后移除外载.目前,孔挤压工艺过程中给出的半径差为0.05~0.10 mm[3],本文通过参数分析给出半径差对残余应力场的影响规律,确定最适合本文300M钢耳片的半径差.模拟分析6种半径差下表面残余应力随距挤入端距离的变化规律,由于结果差别很小,分布规律与图6(b)类似,不再给出趋势图.如图11所示为6种半径差下的挤入端应力分布示意图.因为经过开缝衬套挤压之后,挤入端残余压应力较小,是危险位置,因此仅给出挤入端应力分布.

模拟结果表明,半径差越大,最大残余压应力越大(由-673.3 MPa增大到-821.8 MPa);最大残余压应力位置由表面往材料内部移动;残余应力梯度及高压应力区域明显增大.由此可以看出,半径差越大,孔边挤压效果越好,在保证回弹量满足耳片尺寸加工精度的前提下应选择大的半径差,因此耳片半径差选择0.1 mm,预制倒圆角半径为0.9 mm.
3 疲劳试验验证
为了验证孔挤压对疲劳寿命的增益效果,采用3组试样进行疲劳试验,分别是:未强化、开缝衬套挤压强化(0.9%~1%挤压量)和开缝衬套挤压强化(0.9%~1%挤压量)与孔边挤压强化结合.试验采用MTS-Landmark370.50疲劳试验机加载,试验环境为试验室空气环境,试验施加的载荷水平为490 MPa,试验结果如表2所示.表中,N50为中值疲劳寿命,n为样本数,p为置信度.
结果表明,经过强化之后,耳片疲劳寿命得到大幅提高.相对于未强化的试样,经过开缝衬套挤压之后,耳片疲劳寿命提高近137%,经过开缝衬套挤压与孔边挤压之后,寿命提高近183%.寿命提高的主要原因如下.1)残余压应力的引入抵消了一部分外加应力,降低了有效外载,提高了疲劳寿命.2)在开缝衬套挤压的基础上,孔边挤压的引入会提高孔边残余压应力及增大高压应力区区域,疲劳裂纹从挤入端萌生的情况比较少,且扩展速率变慢.如图12所示为3种情况下的典型断口照片.可以看出,孔边挤压的引入使容易从孔边萌生的小角裂纹变成了从接近耳片厚度一半处萌生的小表面裂纹,说明孔边挤压的引入能够有效防止裂纹从孔边萌生,提高疲劳寿命.
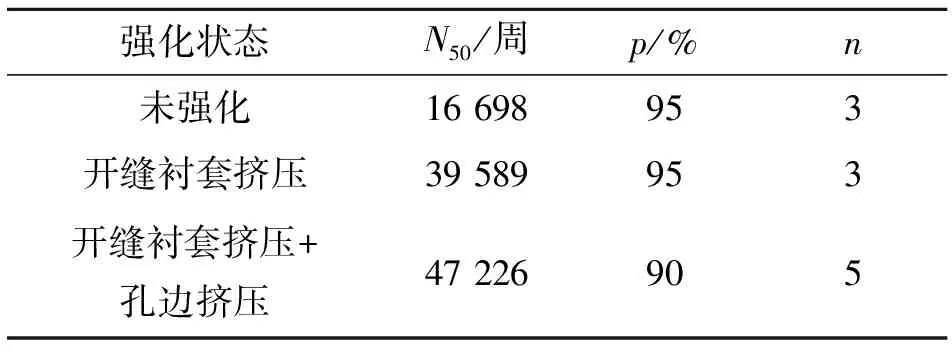
表2 疲劳试验结果
4 结 论
(1)铰孔之后,残余应力重新分布,在有限范围内,铰削量越大,在相同物理位置残余压应力增大越明显,但是减小表面残余压应力会降低材料的疲劳性能.

图12 耳片疲劳试验断口照片Fig.12 Fracture surfaces of lug specimens
(2)在开缝衬套挤压的基础上,进行孔边挤压会提高孔边残余压应力及增大高压应力区区域,提高疲劳性能.半径差越大,孔边挤压效果越好,在保证材料回弹量能够满足设计尺寸精度的条件下,应尽量取较大的半径差.
(3)疲劳试验结果表明,经过开缝衬套挤压强化及开缝衬套挤压与孔边挤压强化之后,耳片疲劳寿命得到显著提高.结合开缝衬套挤压与孔边挤压后,寿命提高更明显.
[1] GOPALAKRISHNA H D, NARASIMHA MURTHY H N, KRISHNA M, et al. Cold expansion of holes and resulting fatigue life enhancement and residual stresses in Al 2024 T3 alloy-an experimental study [J]. Engineering Fail Analysis, 2010, 17(2): 361-368.
[2] CHAKHERLOU T N, SHAKOURI M, AGHDAM A B, et al. Effect of cold expansion on the fatigue life of Al 2024-T3 in double shear lap joints: experimental and numerical investigations [J]. Materials and Design, 2012, 33: 185-196.
[3] HB/Z 170-2005.航空金属零件孔挤压强化工艺[S].北京:中国航空综合技术研究所, 2005.
[4] NIGRELLI V, PASTA S. Finite-element simulation of residual stress induced by split-sleeve cold-expansion process of holes [J]. Journal of Materials Processing Technology, 2008, 205(1-3): 290-296.
[5] WU H. On the prediction of initiation life for fatigue crack emanating from small cold expanded holes [J]. Journal of Materials Processing Technology, 2012, 212(9): 1819-1824.
[6] WEN S Z, LIU C Y, WU R L, MA C L. Effect of cold expansion on high cycle fatigue of aluminum alloy straight lugs [J]. Rare Metal Materials and Engineering, 2015, 44(10): 2358-2362.
[7] YAN W Z, WANG X S, GAO H S, et al. Effect of split sleeve cold expansion on cracking behaviors of titanium alloy TC4 holes [J]. Engineering Fracture Mechanics, 2012, 88: 79-89.
[8] KARABIN M E, BARLAT F, SCHULTZ R W. Numerical and experimental study of the cold expansion process in 7085 plate using a modified split sleeve [J]. Journal of Materials Processing Technology, 2007, 189(1-3): 45-47.
[9] 刘晓龙,高玉魁,刘蕴韬,等.孔挤压强化残余应力场的三维有限元模拟和试验研究[J].航空材料学报,2011, 31(2): 24-27. LIU Xiao-long, GAO Yu-kui, LIU Yun-tao, et al. 3D finite element simulation and experimental test on residual stress field by hole cold expansion [J]. Journal of Aeronautical Materials, 2011, 31(2): 24-27.
[10] 欧阳小穗,张晓晶,杨树勋.孔挤压强化有限元分析及疲劳寿命估算[J].科学技术与工程,2011, 11(12): 2787-2790. OUYANG Xiao-sui, ZHANG Xiao-jing, YANG Shu-xun. Finite element analysis and fatigue life prediction of cold expansion [J]. Science Technology and Engineering, 2011, 11(12): 2787-2790.
[11] YUAN X, YUE Z F, WEN S F, et al. Numerical and experimental investigation of the cold expansion process with split sleeve in titanium alloy TC4 [J]. International Journal of Fatigue, 2015, 77: 78-85.
[12] MAHENDRA BABU N C, JAGADISH T, RAMACHANDRA K, et al. A simplified 3-D finite element simulation of cold expansion of a circular hole to capture through thickness variation of residual stresses [J]. Engineering Failure Analysis, 2008, 15(4):339-348.
[13] LIU Y S, SHAO X J, LIU J, et al. Finite element method and experimental investigation on the residual stress fields and fatigue performance of cold expansion hole [J]. Materials and Design, 2010, 31(3): 1208-1215.
[14] PASTA S. Fatigue crack propagation from a cold-worked hole [J]. Engineering Fracture Mechanics, 2007, 74(9): 1525-1538.
[15] WANG Z, ZHANG X. Predicting fatigue crack growth life for cold-worked holes based on existing closed-form residual stress models [J]. International Journal ofFatigue, 2003, 25(9-11): 1285-1291.
Numerical simulation of whole process of cold expansion in 300M steel lug
HE Zhi-ming1, ZHANG Xiao-jing1, LIU Tian-qi2, YANG Shu-xun1
(1.SchoolofAeronauticsandAstronautics,ShanghaiJiaotongUniversity,Shanghai200240,China;2.AVICBeijingInstituteofAeronauticalMaterials,Beijing100095,China)
A developed finite element model of 300M steel lug was used to analyze the effects of split-sleeve expansion, reaming and hole edge expansion on residual stress field based on three-dimensional nonlinear finite element method. The predicted stress fields accorded with the experimental results. The simulation method was verified feasible. The simulation had highlighted the effects of the reserved round radius and the reaming cuttings weight on the residual stress field. The simulation results were verified by the fatigue tests and the fracture surfaces. Fatigue test results show that the fatigue life increases by 137% after split-sleeve cold expansion and reaming process and the hole edge expansion will improve fatigue life by 183%.
cold expansion; residual stress; finite element analysis; fatigue life
2015-09-08. 浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng
何志明(1991—),男,硕士生,从事结构疲劳与断裂的研究.ORCID: 0000-0002-3442-2821. E-mail: hzm093518@163.com 通信联系人:张晓晶,女,副教授. ORCID: 0000-0003-0958-472X. E-mail: zhangxj76@sjtu.edu.cn
10.3785/j.issn.1008-973X.2016.04.025
TG 376
A
1008-973X(2016)04-0783-09

