杯形柔轮谐波传动三维双圆弧齿廓设计

王家序, 周祥祥, 李俊阳, 肖 科, 周广武

(1. 重庆大学 机电传动与运载装备研究所,重庆 400044; 2. 四川大学 空天科学与工程学院,四川 成都 610065)



杯形柔轮谐波传动三维双圆弧齿廓设计

王家序1,2, 周祥祥1, 李俊阳1, 肖 科1, 周广武2

(1. 重庆大学 机电传动与运载装备研究所,重庆 400044; 2. 四川大学 空天科学与工程学院,四川 成都 610065)

为了提高装置的啮合性能,以公切线式双圆弧齿廓作为研究对象,基于柔轮装配变形及改进运动学理论获得单截面内的谐波传动精确共轭理论,建立共轭齿廓优化设计模型.考虑柔轮变形倾角的影响,采用合理调整柔轮轮齿径向位置的方法设计满足空间啮合要求的三维双圆弧齿廓谐波传动装置,开展计算机仿真分析及实验观察研究.结果表明,双圆弧齿廓谐波传动存在有效的共轭区域及有效的共轭齿廓.为了满足空间啮合要求,柔轮轮齿各截面所需调整的径向位置量与该截面至主截面间的距离成线性关系变化.设计的齿廓在主截面完全啮合,沿轴向其余截面部分啮合,仿真结果与实验观察结果基本吻合,说明了该设计的合理性.

谐波传动；变形倾角；双圆弧齿廓；空间啮合

由于谐波传动[1]具有体积较小、传动精度较高、重合度较大等优点,已被广泛应用于金属机床、半导体制造设备、通信设备等诸多领域,尤其在要求减速器具有小体积、质量轻等特点的机器人及航空航天领域中,谐波传动尤其重要.与传统齿轮传动相区别[2-3],谐波传动中柔轮与刚轮齿数相差2n(n为整数),波发生器迫使柔轮产生周期性可控弹性变形,从而实现柔轮与刚轮的啮合传动.由于选用杯形柔轮,当波发生器装入柔轮后,柔轮会产生一个变形倾角,致使沿轮齿轴向的各截面具有不同的变形量[4],因此,柔轮与刚轮在某一截面虽然保持了良好的啮合状态,但沿轴向其余截面会产生啮合干涉或没有啮合等现象.柔轮倾角随着柔轮轴向尺寸的减小而增大,导致柔轮轮齿与刚轮轮齿之间的接触面积减小,同时柔轮应力急剧增大.在齿廓研究方面,辛洪兵[5]提出基于改进运动学的谐波传动双圆弧齿廓设计方法.Chen等[6]研究分析谐波传动单截面内双圆弧齿廓参数的影响规律；于鹏飞等[7-8]采用有限元方法提出一种刚轮采用斜齿的双圆弧齿廓谐波传动,虽然在一定程度上避免了谐波传动的齿廓啮合干涉,但对于理论分析方法的研究不完善；张勇[9]采用拼接而成的分段不规则的共轭曲线作为刚轮齿廓,刚轮齿廓加工难度较大且各截面啮合区域较小；多数研究集中于解决柔轮轮齿与刚轮轮齿在单截面内的啮合问题,对于考虑柔轮倾角影响的三维齿廓设计研究较少[10-11].对于高刚度、高精度、高承载能力的谐波传动需求十分迫切,为了实现上述需求,本文以公切线双圆弧齿廓作为谐波传动齿廓,基于柔轮装配变形[12]与改进运动学理论[13]提出谐波传动共轭齿廓设计方法.在不采用轮齿磨削、切削、修形等方法的前提下,考虑柔轮变形倾角的影响,设计一种在主截面完全啮合,同时沿轴向其余截面部分啮合的三维双圆弧齿廓.为了验证设计合理性,采用MATLAB仿真分析[14-16]及实验观察等方法对所设计的三维双圆弧齿廓谐波传动的轮齿啮合情况进行分析研究.

1 共轭齿廓求解

1.1 共轭齿廓设计

图1 柔轮齿廓坐标系Fig.1 Coordinate of tooth profile of flexspline

1.1.1 单截面齿廓参数方程 如图1所示,在柔轮轮齿的每一个轴向截面内,建立动坐标系{X1,O1,Y1},其中Y1为柔轮轮齿对称轴,原点O1为Y1轴与中性层曲线的交点,各参数如表1所示.根据双圆弧齿廓的分段特征,以齿廓弧长s为参数对双圆弧齿廓函数进行分段描述如下.

表1 柔轮齿廓参数

Tab.1 Parameter definition of tooth profile of flexspline

符号意义ha齿顶高h全齿高ρa凸齿齿廓圆弧半径ρf凹齿齿廓圆弧半径hl公切线长度ds齿根圆与中性层距离δL齿形工艺角(公切线倾角)αa齿顶压力角

右侧AB段凸齿廓的表达式为

(1)

式中：αa=arcsin ((ha+Ya)/ρa),

xoa=-la,yoa=h-ha+ds-Ya.

右侧BC段切线齿廓的表达式为

(2)

右侧CD段凹齿廓的表达式为

(3)

式中：xof=πm/2+lf,yof=h-ha+ds+Yf.

1.1.2 基于改进运动学的单截面啮合理论 以竖直方向为Y2轴,以刚轮回转中心O2为原点建立刚轮固定坐标系{O2,X2,Y2}.以波发生器长轴为Y轴,以波发生器回转中心O为原点,建立波发生器动坐标系{O,X,Y}.谐波传动中,单截面内波发生器、柔轮、刚轮的运动关系如图2所示,各参数如表2所示.

图2 谐波传动坐标系Fig.2 Coordinate of harmonic drive

符号意义ωH波发生器角速度φH波发生器转角φ1柔轮啮合轮齿矢径与波发生器长轴夹角φ波发生器长轴相对于柔轮未变形端转过的角度ω径向位移ν切向位移μ法向转角ρ柔轮中性层曲线变形后矢径Δφ柔轮啮合轮齿与竖直方向夹角βΔφ-μ

杯形柔轮在单截面内的啮合情况与环形柔轮的啮合情况相似,因而基于改进运动学的谐波啮合理论适用.按照基于改进运动学的谐波啮合理论[13]可知,谐波传动满足的基本啮合方程为

(4)

求解式(4)时需要先解出φ1的表达式,根据中性层曲线不伸长的条件[12],φ1由下面积分关系确定：

(5)

式(5)中求解φ1关于φ的表达式需要求解积分方程,无法给出解析表达式,因而式(4)的求解只能得出近似的数值解.

由于柔轮的装配变形使得谐波传动中两齿廓的实际共轭位置在φ1处,在基于改进运动学谐波啮合理论的基础上,采用参数变换的方法.以φ1为自变量,求解φ1位置上的共轭齿廓,所有参数均表示为φ1的函数.φ关于φ1的导数关系为

(6)

式(4)可以表示为

(7)

φ与φH的函数关系为

φ=φF+φH=(z2/z1)φH.

(8)

式中：z2为刚轮齿数,z1为柔轮齿数.

将式(8)代入式(7),可得

(9)

式(9)是基于柔轮装配变形与改进运动学的谐波啮合理论精确计算方程.将柔轮齿廓的函数表达式(1)～(3)及相应截面在波发生器作用下的变形量代入式(9),可以求出柔轮齿廓与刚轮齿廓共轭时φ1的精确解,满足式(9)的φ1所组成的区域称为共轭区域,与共轭区域对应的齿廓称为共轭齿廓.

1.2 空间啮合三维双圆弧齿廓设计

考虑到谐波齿轮传动的实际工作特性,对设计模型作出如下基本假设[17].

1) 在传动工作过程中,柔轮的中性层曲线长度不变.

2) 柔轮在工作过程中,轮齿形状不变,只有齿槽中部发生变形.

3) 柔轮所有特征圆都是柔轮中性层曲线的等距曲线.

柔轮在装入波发生器前、后的变形状态如图3所示.如图3(a)所示为柔轮未变形时的状态,如图3(b)、(c)所示分别为柔轮装入波发生器后柔轮长轴、短轴处的变形状态.由图3可知,柔轮在装入波发生器后在长轴附近产生外张倾角,在短轴附近产生内张倾角,因此,柔轮在变形后沿轴向各截面(如图3的截面1～5)具有不同的变形量.

为了避免刚轮与柔轮在轴向不同变形量作用下导致的啮合干涉,选取任意一垂直于轴向的截面为设计截面(主截面).基于上述单截面啮合理论设计主截面轮齿齿廓,通过合理调整各截面柔轮齿廓的径向位置,设计满足空间啮合要求的三维双圆弧齿廓.以模数0.5、柔轮齿数200、刚轮齿数202的单级100型谐波传动为例,设计工况为刚轮固定,柔轮输出,波发生器输入,据该设计满足该谐波传动的空间啮合三维双圆弧齿廓.

选用标准椭圆凸轮波发生器,极坐标方程为

(10)

式中：ρ为椭圆矢径,a、b分别为椭圆的长半轴与短半轴,φ为椭圆矢径与长轴的夹角.

柔轮中性层曲线在椭圆凸轮波发生器作用下的径向位移w、切向位移v和法向转角μ分别为

w=ρ-rb,

(11)

v=-∫wdφ,

(12)

μ=-arctan(ρ′/ρ).

(13)

式中：rb为柔轮中性层曲线未变形时的等效圆半径.

求解式(9)所需的参数全部已知,代入相应参数可以求出对应的共轭区域及共轭齿廓.

图3 柔轮变形状态图Fig.3 Deformation state of flexspline

1.2.1 主截面齿廓设计 选取图3中的截面3为设计主截面,该截面的径向变形量为0.537 5 mm,柔轮壁厚为1.25 mm,中性层曲线半径为48.875 mm.柔轮主截面双圆弧齿廓廓形如图1所示,影响双圆弧齿廓廓形的基本参数如表3所示.基于上述共轭齿廓设计方法求解共轭区域及共轭齿廓,如图4、5所示.

表3 柔轮基本齿廓参数

图4 共轭区域Fig.4 Conjugate existent domain

图5 共轭齿廓Fig.5 Conjugate tooth profile

由图4可知,公切线双圆弧齿廓存在2个共轭区域,沿横坐标方向,每个共轭区域从左到右均由3部分组成,依次与柔轮凸齿廓、切线齿廓、凹齿廓对应.沿纵坐标方向,共轭角度较小的区域称为共轭区域1(如曲线1、2、3),共轭角度较大的区域称为共轭区域2(如曲线1″、2″、3″).过横轴上一点作垂线,与共轭区域存在2个交点(如点A、B),即柔轮齿廓上同一点在2个角度均可以产生共轭啮合；过纵轴上一点作水平线,与共轭区域存在2个交点(如点C、D),即柔轮齿廓上存在两点在同一角度均产生共轭啮合,上述现象称为双圆弧齿廓谐波传动的“双共轭”现象.

图4中共轭区域曲线1、1″、2、2″、3、3″依次与图5中共轭齿廓曲线TP1、TP1″、TP2、TP2″、TP3、TP3″对应.如图5所示,为了避免齿廓啮合干涉,只能选取共轭齿廓曲线TP1、TP2、TP3作为刚轮齿廓数值解,称为有效共轭齿廓.此时,对应于图4中只有共轭区域曲线1、2、3为有效共轭区域,因此该双圆弧齿廓谐波传动共轭区域范围很小.若可使得共轭齿廓TP3与TP1″重合,则对应图4中共轭区域为1、1″、2、3,可以显著地提高啮合区域范围,同时保证双共轭现象存在,有效地提高谐波传动重合度.

以共轭齿廓TP3与TP1″重合为优化设计目标,通过对双圆弧齿廓参数(ρa、ρf、hl、δL)的影响规律分析[6]可知,在保证轮齿不产生啮合干涉的条件下,尽可能增大共轭区域,从而优化柔轮双圆弧齿廓参数.优化设计后的柔轮齿廓齿形的基本参数如表4所示,对应的效共轭齿廓如图6所示,其中共轭齿廓TP3与TP1″的重合最大误差为0.002 mm.选取图6中的共轭齿廓作为设计刚轮齿廓所需的数值解.

表4 优化后柔轮基本齿廓参数

图6 优化齿廓有效共轭齿廓Fig.6 Effective conjugate tooth profile with optimizedparameters

1.2.2 其余截面齿廓设计 各截面均采用主截面齿廓,为了避免其余截面产生啮合干涉,须保证其余各截面共轭齿廓均位于主截面共轭齿廓区域以内(见图6的阴影部分),称为条件1.为了避免其余截面没有齿廓啮合的现象,须保证各截面共轭齿廓中至少有一段与主截面共轭齿廓重合(即产生部分啮合),称为条件2.以同时满足条件1、2为优化设计目标,设计满足空间啮合的三维双圆弧齿廓.

1)主截面位置为齿宽中间.

取图3(a)中轮齿截面1、2、3(主截面)、4、5作为研究对象,基于MATLAB参数化编程计算后得到各截面齿廓须调整的径向位置调整量H1及对应的各截面距柔轮底端距离S1、截面柔轮壁厚D1、中性层曲线半径R1,如表5所示.各截面共轭齿廓曲线在主截面上的投影如图7所示,对应的共轭区域如图8所示.

表5 调整量(截面3为主截面)

由表5可知,研究截面1、2、4、5对应的柔轮轮齿所需调整的径向位置量(受D1、R1控制)分别与截面1、2、4、5至主截面间的距离成线性关系变化.根据该线性关系可以求出柔轮轮齿沿轴向任意截面所需调整的径向位移量,设计出如图9所示满足空间啮合要求的三维双圆弧齿廓,此时轮齿呈现中间高、两端低的形式.

图7 共轭齿廓投影图(截面3)Fig.7 Projection of conjugate tooth profile on section 3

图8 共轭区域投影图(截面3)Fig.8 Projection of conjugate existent domain on section

图9 轮齿调整图(截面3为主截面)Fig.9 Tooth of flexspline after adjustment (section 3 is main section)

由图7可知,截面1只存在2条共轭齿廓(TPH1、TPH1″),且均位于主截面齿廓区域内,从而避免了截面1齿廓啮合干涉.两条共轭齿廓分别对应于柔轮凸齿廓在共轭区域1、共轭区域2的共轭曲线H1及H1″(见图8),其中共轭齿廓TPH1″与主截面齿廓基本重合,最大重合误差为0.003 mm,保证了截面1轮齿具有部分啮合的特点,共轭齿廓TPH1″称为该截面的有效共轭齿廓.截面5存在6条共轭齿廓,只有共轭齿廓TPQ1、TPQ2、TPQ3为有效共轭齿廓,分别对应于柔轮凸齿廓、切线齿廓、凹齿廓在共轭区域1的共轭曲线Q1、Q2、Q3.同理得出,截面2、4的共轭齿廓特性与截面1、5相似.

2)主截面位置为齿宽前端.

取截面5(主截面)、4、3、2、1作为研究对象,同理,得到各截面齿廓须合理调整的H1及对应的S1、D1、R1,如表6所示.各截面共轭齿廓曲线在主截面上的投影如图10所示,对应的共轭区域如图11所示.

图10 共轭齿廓投影图(截面5)Fig.10 Projection of conjugate tooth profile on section 5

图11 共轭区域投影图(截面5)Fig.11 Projection of conjugate existent domain onsection 5

截面位置S1/mmH1/mmD1/mmR1/mm主截面810．001．2548．875中前端4760．031．2248．860中间截面3710．061．1948．845中后端2660．091．1648．830后端截面1610．121．1348．815

由表6可知,研究截面1、2、3、4对应的柔轮轮齿所需调整的径向位置量分别与截面1、2、3、4至主截面之间的距离成线性关系变化.同理设计出满足空间啮合的三维双圆弧齿廓,如图12所示,此时轮齿呈现前端高、后端低的锥齿轮形式.

3)主截面位置为齿宽后端.

截面1为主截面可以得到与上述结论相似的结果,则研究截面5与3的齿廓须合理调整的H1及对应的S1、D1、R1,如表7所示.截面5、3、1的共轭齿廓曲线在主截面1上的投影如图13所示,对应的共轭区域如图14所示,设计出满足空间啮合的三维双圆弧齿廓如图15所示,此时轮齿呈现后端高、前端低的锥齿轮形式.

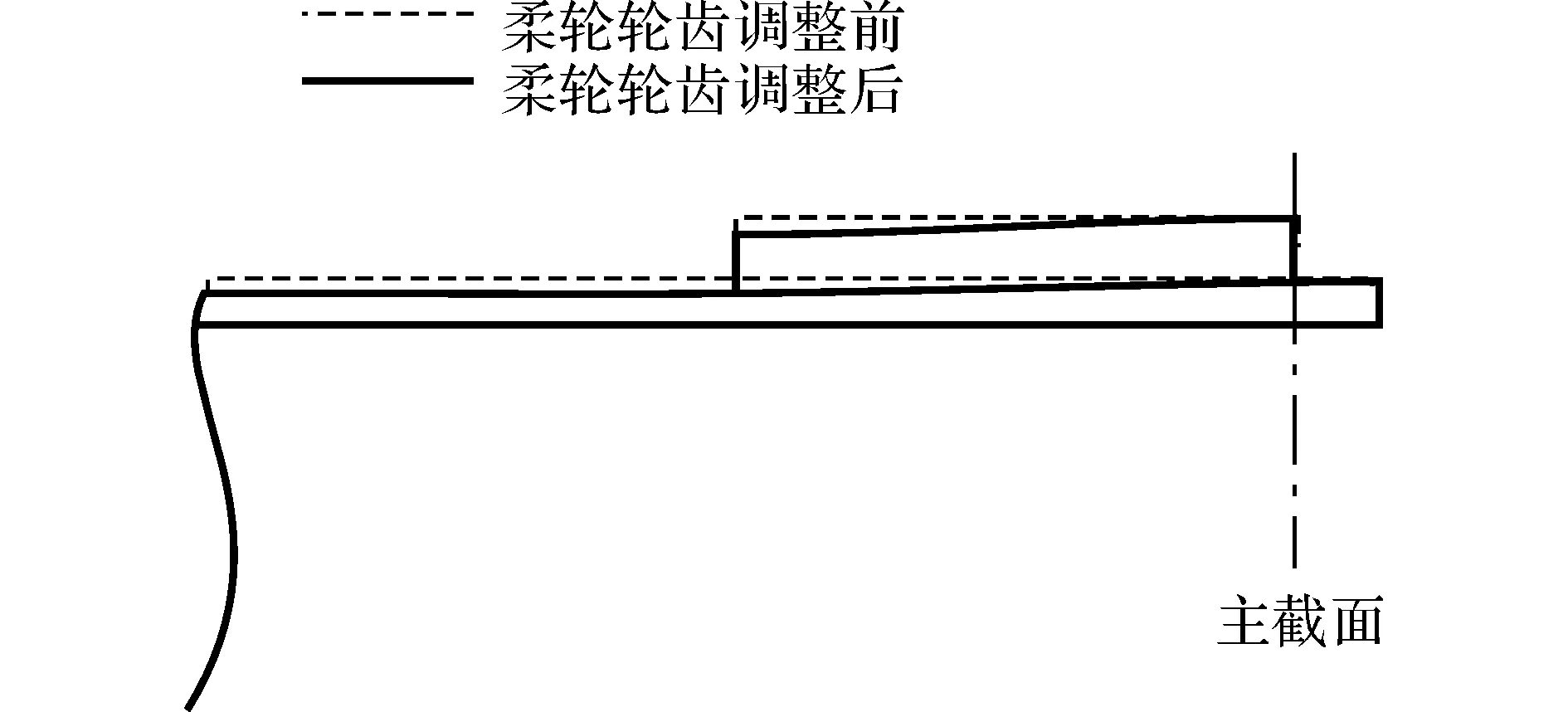
图12 轮齿调整图(截面5为主截面)Fig.12 Tooth of flexspline after adjustment (section 5 is main section)

截面位置S1/mmH1/mmD1/mmR1/mm前端截面5810．251．0048．7500中间截面3710．1251．12548．8125主截面610．001．2548．8750

图13 共轭齿廓投影图(截面1)Fig.13 Projection of conjugate tooth profile on section 1

图14 共轭区域投影图(截面1)Fig.14 Projection of conjugate existent domain on section 1

图15 轮齿调整图(截面1为主截面)Fig.15 Tooth of flexspline after adjustment (section 1 is main section)

综上所述,柔轮轮齿任意截面所需调整的径向位置量、柔轮壁厚、中性层曲线半径均与该截面至主截面间的距离成线性关系变化；当主截面为轮齿中间截面时有效共轭齿廓、有效共轭区域较大,主截面为前端时次之,主截面为后端时较小.

2 啮合分析

以柔轮轮齿中间截面为主截面进行齿廓设计,设计的柔轮齿廓参数如表4所示,柔轮轮齿沿轴向各截面的径向修形量如表5所示,求解共轭齿廓并进行圆弧拟合后得到对应的刚轮齿廓如图16所示,齿廓参数如表8所示.

图16 刚轮齿形Fig.16 Tooth profile circular spline

变量变量值/mm变量变量值/mmha0．400ρa0．80hf0．565hl0．06ρf0．700δL6．55°

2.1 运动轨迹分析

为了验证上述分析的合理性,对具有上述双圆弧齿廓的柔轮及刚轮啮合情况基于MATLAB进行仿真分析,得到柔轮轮齿相对于刚轮齿槽的运动轨迹,如图17所示.如图18所示为相同参数柔轮轮齿未采用径向位置调整时前端截面及后端截面的运动轨迹图.

图17 各截面运动轨迹图(调整后)Fig.17 Relative movement trail (after adjustment)

图18 各截面运动轨迹图(未调整)Fig.18 Relative movement trail (before adjustment)

由图17可知,各截面轮齿均无啮合干涉.在轮齿前端截面,柔轮轮齿与刚轮凹齿廓产生部分啮合；在轮齿后端截面,柔轮轮齿与刚轮凸齿廓始终保持连续啮合,在轮齿主截面,柔轮轮齿与刚轮轮齿始终保持连续啮合.所设计的三维双圆弧齿廓具有在主截面保持完全啮合、同时沿轴向其余任意截面均保持部分啮合的特点,有效避免了谐波传动的齿廓啮合干涉.

由图18可知,若仅进行主截面齿廓设计,则除主截面齿廓连续啮合且不产生干涉外,其余截面齿廓均会产生大小不一的干涉量.

2.2 装配状态分析

设定与波发生器长轴对应的柔轮轮齿为1号轮齿,往右依次为2, 3, …,N号轮齿,如图19所示为本文所设计柔轮轮齿在前端截面5、中间截面3、后端截面1与刚轮轮齿的相对位置图.由图19可知,各截面均无啮合干涉且啮合状态良好,且各截面轮齿状态与图17所示的运动轨迹状态基本吻合,说明了设计分析的正确性及合理性.

图19 各截面仿真装配啮合图Fig.19 Assemble engagement condition of simulation on different section

3 实验观察

为了从实验角度进一步验证上述理论分析的合理性,将中间截面为主截面的设计实例进行实体加工,得到谐波减速器装配实体.利用显微镜对谐波传动轮齿前端截面5的啮合情况进行观察后,得到该截面的轮齿啮合状态,如图20所示.

图20 实验啮合状态图(截面5) Fig.20 Assemble engagement condition of experiment on section 5

对比图20的实验观察结果与图17(a)、19的理论仿真结果可知,在轮齿前端截面,柔轮轮齿进入刚轮齿槽的初始阶段,柔轮轮齿与刚轮齿槽均有较大的侧隙；在中间阶段,侧隙减小；在完成阶段,柔轮轮齿与刚轮齿槽完全啮合,实验观察结果与仿真结果基本吻合,说明了该设计的有效性.

4 结 论

(1) 基于柔轮装配变形与改进运动学理论,获得了一种谐波传动的精确啮合分析方法,发现双圆弧齿廓的有效共轭区域及有效共轭齿廓.

(2) 通过改变柔轮轮齿径向位置可以有效地避免齿廓啮合干涉并提高谐波传动重合度,且所需调整的径向位置量与研究截面至主截面间的距离成线性关系变化.

(3) 主截面为轮齿中间截面时有效共轭齿廓、有效共轭区域较大,主截面为前端时次之,主截面为后端时较小.

(4) 采用中间截面为主截面,设计了主截面完全啮合、轴向其余截面部分啮合的三维双圆弧齿廓.仿真结果与实验观察结果基本吻合,说明了本文设计的合理性.

[1] MUSSER C. Strain wave gearing: US, 2,906,143 [P]. 1959-09-29.

[2] 王建,罗善明,苏德瑜.基于压力角的高重合度齿轮主动设计及特性分析[J]. 中南大学学报：自然科学版,2014,45(11): 3792-3799. WANG Jian,LUO Shan-ming,SU De-yu. Active design and characteristics analysis of high contact ratio gears based on pressure angle [J]. Journal of Central SouthUniversity: Science and Technology,2014,45(11):3792-3799.

[3] 杨富春,周晓军,胡宏伟. 两级齿轮减速器非线性振动特性研究[J]. 浙江大学学报：工学版,2009,43(7):1243-1248. YANG Fu-chun,ZHOU Xiao-jun,HU Hong-wei. Nonlinear vibration characteristics of two-stage gear reducer [J]. Journal of Zhejiang University: Engineering Science,2009,43(7): 1243-1248.

[4] ISHIKAWA S. Wave gear device: US, 8,215,205B2 [P]. 2012-07-10.

[5] 辛洪兵. 双圆弧谐波齿轮传动基本齿廓设计[J]. 中国机械工程, 2011, 22(6): 656-662. XIN Hong-bing. Design for basic rack of harmonic drive with double-circular-arc tooth profile [J]. ChinaMechanical Engineering, 2011, 22(6): 656-662.

[6] CHEN Xiao-xia, LIU Yu-sheng, XING Jing-zhong, et al. The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive [J]. Mechanism and Machine Theory, 2014, 73 (3): 1-24.

[7] 吴伟国, 于鹏飞, 侯月阳. 短筒柔轮谐波齿轮传动新设计新工艺与实验[J]. 哈尔滨工业大学学报, 2014,46(1): 40-46. WU Wei-guo,YU Peng-fei,HOU Yue-yang. New design, new process of harmonic drive with short flexspline and its experiment [J]. Journal of Harbin Institute of Technology, 2014,46(1): 40-46.

[8] 于鹏飞.机器人用短筒柔轮谐波减速器研制与性能测试[D].哈尔滨: 哈尔滨工业大学,2012: 16-18. YU Peng-fei. Research on harmonic drive with short flexspline for robot and its experiment studies [D]. Harbin: Harbin Institute of Technology,2012: 16-18.

[9] 张勇. 仿人机器人用1/4比例柔轮谐波传动啮合理论与分析[D]. 哈尔滨: 哈尔滨工业大学,2011: 17-19. ZHANG Yong. Meshing theory and analysis of harmonic transmission with 1/4 short flexspline for humanoid robot [D]. Harbin: Harbin Institute of Technology,2011: 17-19.

[10] 范元勋, 王华坤, 宋德锋. 谐波齿轮传动共轭齿廓的计算机数值模拟研究[J]. 南京理工大学学报, 2002, 26 (4): 389-392. FAN Yuan-xun, WANG Hua-kun, SONG De-feng. Research on computer simulation for conjugate tooth profiles of the harmonic drive [J]. Journal of Nanjing University of Science and Technology, 2002, 26(4):389-392.

[11] OGUZ K, FEHMI E. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modeling [J]. Materials and Design, 2007, 28(2): 441-447.

[12] 陈晓霞, 林树忠, 邢静忠, 等. 基于挠性构件变形的谐波齿轮装配模型[J]. 计算机集成制造系统, 2011,17(2): 338-343. CHEN Xiao-xia, LIN Shu-zhong, XING Jing-zhong, et al. Assembly model of harmonic gear based on elastic component deformation [J]. Computer Integrated Manufacturing Systems, 2011,17(2): 338-343.

[13] 辛洪兵. 研究谐波齿轮传动啮合原理的一种新方法 [J]. 中国机械工程, 2002, 13(3): 181-183. XIN Hong-bing. A new method for research onengagement algorithm of harmonic drive [J]. China Mechanical Engineering, 2002, 13(3): 181-183.

[14] 陈晓霞, 林树忠, 邢静忠, 等. 圆弧齿廓谐波齿轮侧隙及干涉检查仿真[J].计算机集成制造系统, 2011,17(3): 643-648. CHEN Xiao-xia, LIN Shu-zhong, XING Jing-zhong, et al. Simulation on gear backlash and interference check of harmonic drive with circular-arc teeth profile [J]. Computer Integrated Manufacturing Systems, 2011, 17(3): 643-648.

[15] DONG Hui-ming. Kinematic effect of the compliant cup in harmonic drives [J]. Journal of MechanicalDesign, 2011, 133(1): 051004.

[16] DONG Hui-ming. Kinematic fundamentals of planar harmonic drives [J]. Journal of Mechanical Design, 2011, 133(1): 011007.

[17] 沈允文,叶庆泰. 谐波齿轮传动的理论和设计[M]. 北京：机械工业出版社, 1985: 53-55.

Three dimensional profile design of cup harmonic drive with double-circular-arc common-tangent tooth profile

WANG Jia-xu1,2,ZHOU Xiang-xiang1, LI Jun-yang1, XIAO Ke1, ZHOU Guang-wu2

(1.InstituteofElectromechanicalTransmissionandDeliveryEquipment,ChongqingUniversity,Chongqing400044,China;2.SchoolofAeronauticsandAstronautics,SichuanUniversity,Chengdu610065,China)

Double-circular-arc common-tangent tooth profile (DCTP) was introduced for the tooth profile of harmonic drive (HD) in order to improve the engagement quality of HD. An exact method and model for effectively designing conjugate tooth profile in a single section based on modified kinematic method and the elastic deformation of flexspline (FS) were presented. A reasonable tooth profile design method was proposed considering the influence of axial inclination angle. The method can maintain the three-dimensional teeth meshing engagement of HD over a wide range by correctly shifting the tooth profile portions of FS. The relative meshing engagement of the HD with three-dimensional DCTP was analyzed by computer simulation and experimental observation methods. Results showed that the effective conjugate existent domain (CED) and conjugate tooth profile (CTP) were found. The amount of shifting in any other section perpendicular to the axis of FS increases in proportion to the distance from the research section to the main section in order to satisfy the three-dimensional engagement requirements. The designed DCTP can maintain the teeth meshing engagement over a wide range in main section and keep a partial meshing engagement in other sections along the axis of FS. The simulation results accorded with the experimental results. The correctness of the design models was effectively proved.

harmonic drive; inclination angle; double-circular-arc tooth profile; dimensional engagement

2015-03-25. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

国家自然科学基金资助项目(51435001, 51375506); 国家“863”高技术研究发展计划资助项目(2015AA043001)；高等学校博士学科点专项科研基金优先发展领域课题资助项目(20120181130012); 重庆市“两江学者”计划专项经费资助项目.

王家序(1954—), 男, 教授, 博导, 从事齿轮传动、机器人驱动机构、机电传动与智能控制等研究. ORCID: 0000-0003-0808-6569. E-mail: jxwang@cqu.edu.cn

10.3785/j.issn.1008-973X.2016.04.004

TH 132

A

1008-973X(2016)04-0616-09