箔条云建模与极化特性仿真技术研究

李尚生,付哲泉,陈佳林

(1 海军航空工程学院电子信息工程系,山东烟台 264001;2 海军装备研究院,上海 200400)



箔条云建模与极化特性仿真技术研究

李尚生1,付哲泉1,陈佳林2

(1 海军航空工程学院电子信息工程系,山东烟台 264001;2 海军装备研究院,上海 200400)

为分析箔条干扰极化特性以及提高制导雷达基于极化特性差别的抗箔条干扰能力,建立不同密度、形状、分布的箔条云空间模型,将电磁场数值计算方法引入到箔条云极化散射特性的计算,计算结果表明箔条云雷达截面积大小与密度成正比,且满足全极化大于同极化、同极化大于交叉极化的规律,同时计算得到了极化散射矩阵各元素数值。研究结论对于建立真实的模拟战场环境、开展雷达的抗极化干扰实验、改善雷达性能具有重要意义。

箔条云;同极化;交叉极化;极化矩阵

0 引言

近代战争中,箔条在掩护飞机编队和保护水面舰艇方面取得了很好的效果,研究箔条干扰回波信号特征显得格外重要。关于箔条干扰雷达回波特性的研究在时域[1-3]和频域[4-6]方面起步早、成效显著,相关研究结论已经得到应用,而回波极化特性研究起步较晚。一般而言,获取箔条云雷达回波极化特性的途径有两个:一是通过试验的方法;二是通过理论分析和仿真的方法。由于现有雷达极化体制的限制,以及外场测试箔条回波信号特征周期长、花费高的原因,通过试验手段获取箔条云团雷达回波信号的极化特性很困难,箔条干扰极化域特性[7-13]的研究主要为对不同状态箔条云散射矩阵统计特征的理论推导计算,不能真实体现箔条干扰的极化信息。针对以上问题,建立箔条云空间分布模型,将电磁场数值计算方法引入到箔条云极化散射特性的计算。

1 箔条云模型的建立

分析箔条云的极化特性,首先要建立合理的箔条云模型。箔条在空中散开时,由于空气流动、箔条间相互碰撞等因素,导致各箔条之间运动状态相差很大。理论和实际测量结果表明,箔条云团在空中炸开后,其形状逐渐由球体变为扁长椭球体,且箔条丝在空中服从均匀或正态分布。

1.1 单根箔条模型的建立

当箔条被电磁波照射时,其表面会产生感应电流,感应电流在箔条的周围产生交变的电磁场,电磁场以波动的形式向外传播,箔条因此往外散射能量,研究表明长度为雷达发射信号波长一半的谐振散射箔条具有最大的散射截面积,但是谐振散射箔条的频带很窄。为了使箔条覆盖较宽的频带,具备同时干扰多频段雷达的能力,一般将不同频率对应的半波长箔条混合包装以满足要求。综合考虑箔条散射截面、频带宽度以及导电性能等因素,选择长度为半波长,长宽比为30,厚度忽略不计的理想金属导体作为箔条。

首先,由ANSYS软件建立单根箔条的模型并进行平面三角形剖分,以频率10GHz对应的半波长箔条为例,剖分结果如图1所示。

图1 频率10 GHz对应的半波长箔条剖分结果图

图1中箔条长度为1.5

cm

,宽度为0.05

cm

,同理可以得到不同频率对应的不同长度箔条剖分模型。

1.2 箔条云模型的建立

实际使用时,箔条弹中箔条数量巨大,逐一对箔条建模的方法将花费很长时间。为了高效的建立箔条云模型,采用先建立不同尺寸单根箔条模型,然后对单根箔条根据空间分布的要求进行旋转、平移的方法提高效率。下面详细叙述箔条云模型建立过程。

对单根箔条而言,箔条模型由长为半波长,长宽比为30的矩形近似,因而箔条的空间位置可以由矩形的4个顶点唯一确定。若箔条云中箔条个数为N,则只需确定对应的4N个顶点坐标,就可以得到所需箔条云模型。若箔条模型的一个顶点坐标为r0=(x0,y0,z0),则第i根箔条对应的顶点可以由r0依次绕x、y、z轴旋转αi、βi、γi角度,然后坐标平移(xi,yi,zi)得到。旋转后的坐标(xsi,ysi,zsi)可以表示为:

(1)

若箔条云在空间服从半径为R的球体均匀分布,则平移坐标(xi,yi,zi)可以表示为:

(2)

式中：r、θi、φi分别服从(0,R)、(0,π)、(0,2π)的均匀分布,因此对应的变换后顶点坐标为:

(x,y,z)=(xsi+xi,ysi+yi,zsi+zi)

(3)

同理可以得到第i根箔条的其他3个顶点坐标,确定第i根箔条的位置。

由于箔条云在空间分布时不会出现两根箔条相交的情况,在建立箔条云模型的过程中需要判断箔条之间是否相交,并舍去相交的箔条。箔条云模型生成之后,就可以导入到ANSYS软件中进行剖分处理。图2和图3分别给出了4 000根箔条在空间服从球体均匀分布和椭球正态分布的模型。其中,4 000根箔条由10GHz和15GHz对应的半波长、全波长箔条各占四分之一组成。图2中箔条云服从半径为1m的球体均匀分布,图3中箔条云服从半径比为1∶1∶2的椭球正态分布。

图2 球体均匀分布箔条云模型

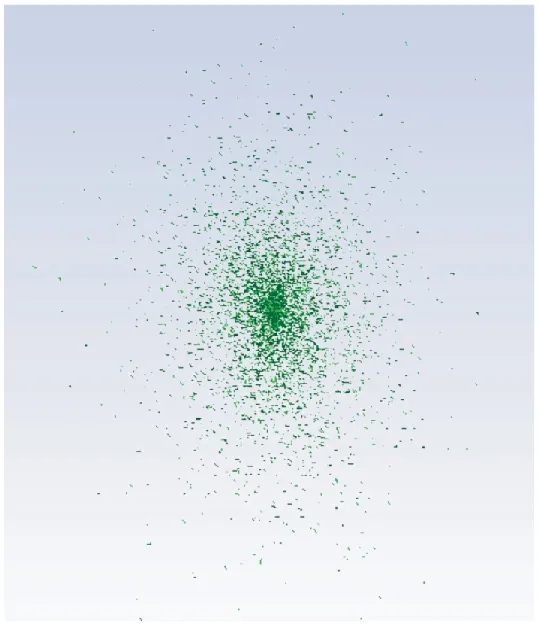
图3 椭球正态分布箔条云模型

2 箔条云回波信号计算与分析

FEKO软件是基于矩量法,对目标三维全波电磁仿真的软件,同时集成多种算法,对计算电大尺寸模型的电磁特性有很大优势。对金属导体(如箔条),FEKO可以计算导体表面的面电流分布,然后计算近场、远场、RCS等参数。将建立好的箔条云模型导入FEKO软件,结合矩量法和快速多极子算法分析箔条云单站远场回波特性。设定入射电磁波为线极化平面波,频率为10GHz,幅度为1V,初相为0°,极化方式为垂直极化,入射角θ=90°(平视)、φ=0°～180°,其中φ间隔角度为5°。分别对4 000根和12 000根在空间服从半径为1m的球体均匀分布箔条云进行计算,结果如图4、图5所示。

图4 箔条云(4 000根)单站远场计算结果

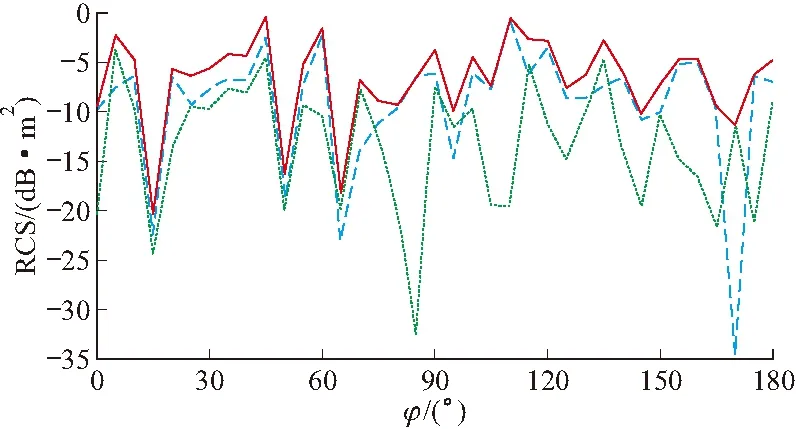
图5 箔条云(12 000根)单站远场计算结果

图中横轴为电磁波入射角,单位为(°);纵轴为雷达截面积(RCS),单位为dBm2。红色实线、蓝色虚线、绿色点状线分别表示全极化、同极化、交叉极化接收时的雷达截面积。对箔条云同一接收极化方式下,不同观察角度得到的雷达散射截面求平均,不同接收极化方式计算结果见表1。

从图表中可以看出不同极化接收时,雷达截面积由大到小依次为全极化、同极化、交叉极化,不同极化方式之间相差2倍左右。对比不同密度箔条云可以看出,随着箔条云密度的变大,雷达截面积也增大。同一极化方式下,两种密度箔条云的雷达截面积相差3倍左右,说明在以上密度范围内箔条云雷达截面积与箔条云密度成正比。

表1 不同接收极化方式时箔条云计算结果

(4)

式中:上标s表示散射电磁波;aHH表示水平极化入射产生水平极化散射场的散射系数;aHV表示水平极化入射产生垂直极化散射场的散射系数。同理,垂直极化照射下目标散射场也可以表示为两部分。四种散射成分分别被水平和垂直极化天线接收,所以有:

(5)

式中:上标r表示天线接收。散射矩阵S可以表示为:

(6)

为全面分析箔条云雷达回波信号极化域特性,得到箔条云的极化散射矩阵。对4 000根箔条构成的箔条云模型,将入射波极化方向改为水平极化,计算结果如图6所示。

图6 水平极化波入射时的箔条云单站远场计算结果

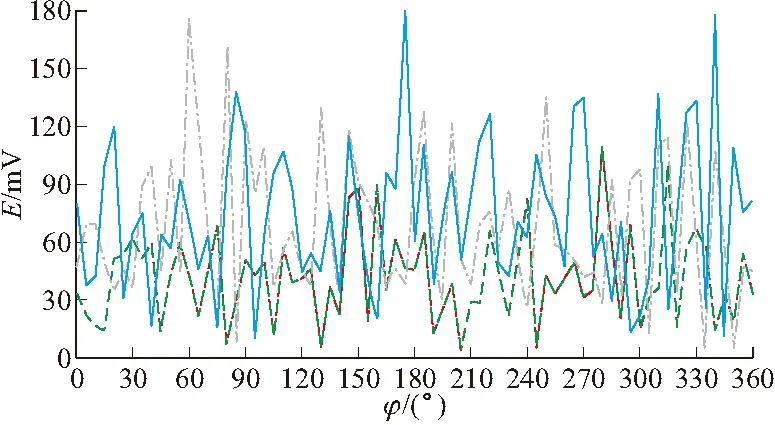
图7 箔条云(4 000根)极化散射矩阵各元素变化图

图6中红色实线、绿色点状线、蓝色虚线分别表示全极化、同极化、交叉极化接收时的雷达截面积。可以看出水平极化入射时,全极化、同极化、交叉极化雷达截面积大小的相对关系与垂直极化入射时一致。垂直和水平极化入射时箔条云的同极化、交叉极化电场幅度值如图7所示,计算结果平均值如表2所示,其中箔条云为4 000根服从半径为0.2m的球均匀分布。

表2 极化矩阵各元素计算结果

由图7可以看出,对同一个箔条云模型而言,不同观察角度得到的交叉极化回波数据完全吻合,与表2计算的平均结果一致,二者相对误差小于0.05%。同时,由图7和表2可以知道,不同观察角度得到的同极化结果不尽相同,但是二者平均值相近,而且同极化回波雷达截面积均在交叉极化回波雷达截面积的4dB以上。

3 结论

文中将电磁场数值计算方法引入到箔条云极化散射特性的计算,建立不同密度、不同形状、不同分布的箔条云空间模型,利用FEKO软件对不同入射角度的箔条云单站远场回波进行计算,分析得到箔条云极化散射特性,结果表明不同接收极化方式箔条云回波雷达截面积各不相同,但满足全极化大于同极化、同极化大于交叉极化的规律,而且在文中箔条云模型密度范围内,雷达截面积大小与箔条云密度成正比。对同一箔条云模型分别改变发射和接收极化方式来分析其极化散射矩阵规律,结果显示同一箔条云模型交叉极化(垂直极化发射水平接收和水平极化发射垂直接收)的雷达截面积完全相同,同时,同极化对应雷达截面积相比于交叉极化要大4dB以上。以上结论可以促进对回波极化域信息的利用,有助于在实验室条件下建立不同状态的箔条云干扰环境,开展雷达的极化抗干扰试验。

[1] 曲长文, 李亚南. 箔条云雷达回波的仿真研究 [J]. 火力指挥与控制, 2012, 37(7): 47-49.

[2] 孙华东. 箔条云团RCS模拟仿真方法研究 [D]. 西安: 西安电子科技大学, 2009.

[3] 李亚飞, 潘莉莉. 基于散射特性的混装箔条云RCS计算与仿真 [J]. 舰船电子工程, 2015, 35(1): 84-87.

[4] 尚炜, 陈伯孝, 蒋丽凤. 基于频谱展宽效应的一种抗箔条方法 [J]. 制导与引信, 2006, 27(3): 5-9.

[5] 陈宁. 箔条云对脉冲多普勒探测系统的干扰机理 [D]. 南京: 南京理工大学, 2013.

[6] 舒欣, 沈福民. 时频分析技术在抑制箔条干扰中的应用 [J]. 西安电子科技大学学报(自然科学版), 2001, 28(5): 676-680.

[7] 李金梁, 王雪松, 李永祯. 正态空间取向箔条云的极化特性 [J]. 电波科学学报, 2008, 23(3): 389-395.

[8] 李永祯, 王雪松, 肖顺平, 等. 自由空间中箔条云团极化散射统计特性的研究 [J]. 电波科学学报, 2004, 19(6): 649-653.

[9] 王雪松, 赫晓峰, 周颖, 等. 自由空间中偶极子云团极化散射特性研究: 相干散射模型 [J]. 电波科学学报, 2001, 16(1): 66-71.

[10] 来庆福, 李金梁, 冯德军, 等. 舰船与箔条的双极化统计特性研究 [J]. 电波科学学报, 2010, 25(6): 1079-1084.

[11] 李金梁, 王雪松, 李永祯. 箔条云散射的极化统计特性 [J]. 电子学报, 2010, 38(3): 714-719.

[12] 章力强, 李相平, 陈信. 箔条假目标干扰极化识别与抑制技术 [J]. 制导与引信, 2012, 33(1): 19-23.

[13] 党晓江, 李政杰, 李欣, 等. 极化捷变末制导雷达抗机载箔条质心干扰研究 [J]. 系统仿真学报, 2014, 26(8): 1807-1813.

Chaff Cloud Modeling and Research on Technology of Polarization Characteristic Simulation

LIShangsheng1,FUZhequan1,CHENJialin2

(1DepartmentofElectronicsandInformationEngineering,NavalAeronauticalandAstronauticalUniversity,ShandongYantai264001,China; 2NavyAcademyofArmament,Shanghai200400,China)

Inordertoanalyzepolarizationcharacteristicsofchaffjammingandimprovecapabilityofanti-chaffjammingofguidanceradarbasedonpolarizationcharacteristicsdifference,chaffcloudmodelofdifferentdensity,shapeanddistributionwasestablished,andthen,electromagneticfieldnumericalcalculationmethodwasintroducedincalculationofchaffcloudpolarizationscatteringcharacteristics.ThecalculationresultsshowthatthechaffcloudRCSisproportionaltodensity,andsatisfyingthelawthatfull-polarizationisgreaterthanco-polarizationandco-polarizationisgreaterthancross-polarization.Atthesametime,fourelementsofthepolarizedscatteringmatrixaregot.Theresearchconclusionsareofgreatsignificanceforbuildingofrealsimulationbattlefieldenvironment,conductingofradarpolarizationinterferenceexperimentandimprovementofradarperformance.

chaffcloud;co-polarization;cross-polarization;polarizationmatrix

2015-07-27

李尚生(1965-),男,山东平阴人,教授,硕士,研究方向:制导雷达技术研究。

TN

A