基于模糊规则的直接力引入时机设计方法

宋广润

(71315部队,河南商丘 476000)



基于模糊规则的直接力引入时机设计方法

宋广润

(71315部队,河南商丘 476000)

为解决在末制导阶段引入直接力控制的时机问题,提出了一种基于模糊规则的设计方法。文中以应用广泛的比例导引律为基础,将剩余时间、目标机动、导弹需用过载、导弹速度这四个影响直接力引入时间的因素综合考虑,对直接力引入时机进行分析,利用模糊规则将四者综合,得到直接力引入时机。通过数字仿真,验证了该设计方法能够有效解决在末制导阶段直接力引入时机问题。

直接力控制;引入时机;模糊规则

0 引言

现阶段精确制导导弹趋于向高速、高机动方向发展,因此导弹的拦截也必须考虑实现对高速、高机动目标的有效打击。由于气动力在响应时间和最大过载方面的限制,出现了利用直接力弥补气动力的不足,提高导弹机动能力的方法。引入直接力需要面对一个很关键的问题,就是直接力何时引入才能够有效的提高机动能力,减小脱靶量。直接力引入过早或过晚都会降低导弹的制导精度[1]。有相关文献提出,可以根据剩余时间、相对距离、导弹需求过载占气动力所能提供最大过载的比例等因素来确定直接力引入时机,而且都具有各自的优势和特点,同时这几种方法也都存在着各种限制[1]。从目前的研究现状来看上述各种因素对于直接力引入时机到底有怎样的影响,对最终的脱靶量有什么影响,现在研究的还比较少,尚没发现精确的模型。所以,考虑一种综合的方法将各种影响到直接力引入时机的因素综合在一起来进行设计并且采用模糊规则的方法来规避没有精确模型的问题是文中的主要思想。

1 直接力引入时机设计方法分析

1.1 常见的设计方法

在引入时机的设计方法上最常见的有根据剩余时间tgo、相对距离和导弹需用过载这3种方法[1-2]。剩余时间由式(1)计算得出:

(1)

式中r为相对距离。

一般情况下都是选用剩余时间为0.5 s附近[2]时引入直接力。

用相对距离选择引入时机时需要考虑导弹的速度,甚至是目标的速度。文中选择相对距离为500 m时启动直接力。

利用导弹需用过载方法一般是通过导弹需用过载占气动力能够提供的最大过载的比例L(见式(2))来选择引入时机。设导弹气动力可提供的最大过载为nmax,导弹需用过载为n,则:

L=n/nmax

(2)

对于L(0≤L≤1)的选取,在其它仿真条件相同的条件下,选取不同的L,得到导弹的脱靶量。根据不同的L对脱靶量的影响,选取脱靶量最小时对应的

L[1],文中L选取0.9。

1.2 综合设计方法

前述3种方法有着各自的特点,仿真结果如表1所示,仿真条件见仿真验证所述。3种方法中以由需用过载设计引入时机效果比较稳定,在目标大机动情况下以剩余时间设计引入时机较好,但是在导弹速度较大时脱靶量比较大。基于此文中在综合设计方法中考虑以剩余时间方法为基础,利用模糊规则来综合导弹需用过载、导弹速度和目标过载因素对引入时机的影响。

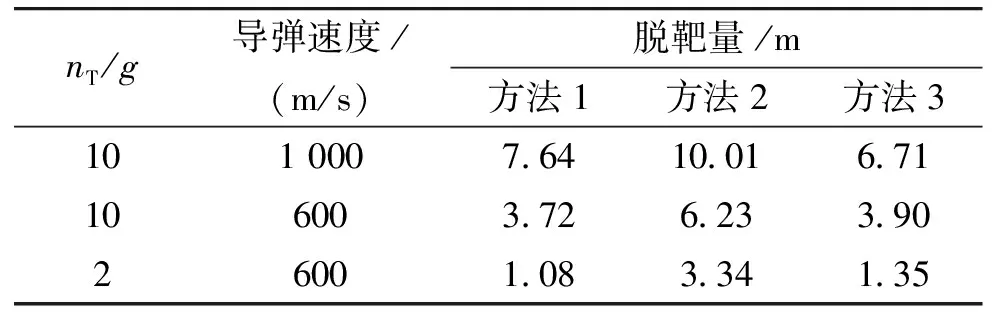
表1 常见的3种设计方法比较

因为剩余飞行时间的选取一般是选择在tgo=0.5 s附近,所以综合设计选用式(3)得到最终直接力引入时间。

tstart=0.5(1-β)+β·tL

(3)

式中:tL为需用过载比例L≥0.9时得到的剩余飞行时间;tstart为直接力启动时剩余飞行时间;β为综合设计系数。

在制导过程中,把得到的tstart与tgo相比较,如果tstart≥tgo,启动直接力,反之按导引律导引飞行。

由式(3)可知综合设计最终变为对于综合设计系数β的选择上。

导弹的速度和目标的机动对于拦截的最终效果有着重要的影响,因而在综合设计中必须考虑导弹的速度和目标机动。两者的影响将利用模糊规则[3-6]体现在β的选择上。

2 构建模糊规则表

模糊规则将导弹的速度和目标的过载作为输入量,β作为输出量。导弹速度V的模糊集为VS(非常小),S(小),M(中),B(大),VB(非常大),隶属函数采用对称的三角函数(见图1)。目标过载nT的模糊集为NB(负大),NM(负中),NS(负小),ZE(零),PS(正小),PM(正中),PB(正大),隶属函数采用对称的三角形函数(见图2)。

输出β的模糊集为Z(零),VS(极小),MS(中小),S(小),SM(小中),M(中),BM(大中),B(大),MB(中大),VB(极大),E(1),其隶属函数见图3。文中模糊蕴含运算采用最小运算规则,清晰化计算使用加权平均法。

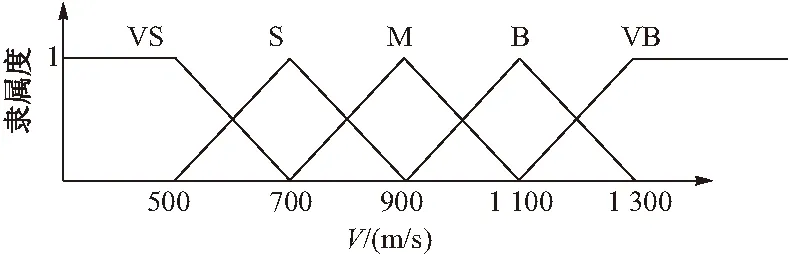
图1 导弹速度隶属度

图2 目标过载隶属度

图3 β隶属度

导弹速度、目标过载、β3者对应进行数字仿真,选择最终使得脱靶量最小的β作为一组导弹速度和目标过载的输出,构成模糊规则表,如表2所示。

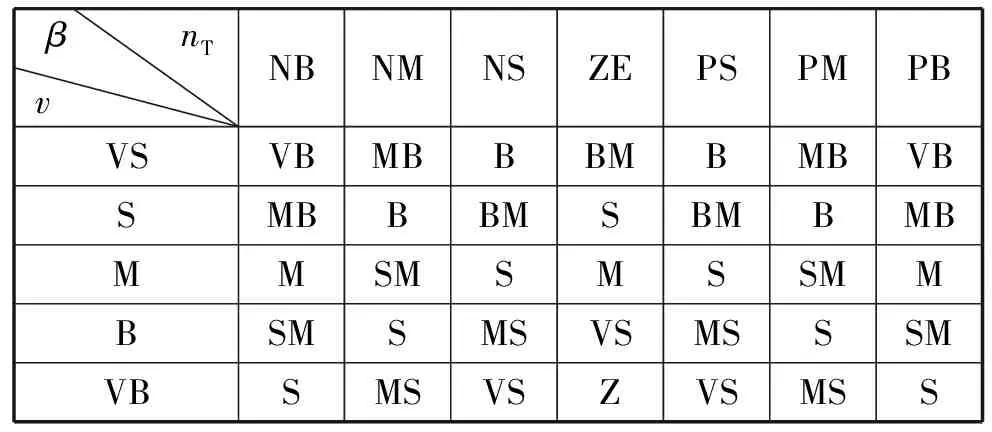
表2 nT、v以及相对应的β模糊规则表

3 仿真验证

仿真以应用广泛的比例导引律为基础,形式如下:

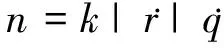
(4)

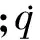
由式(4)可以看出,根据导弹需求过载得到的tL是与视线转率相关联的。

仿真条件假设:目标的速度为400 m/s,末制导开始距离为3 000 m,气动力提供最大过载为3g,直接力为导弹提供气动力无法达到的附加过载,持续时间一定。假设导弹为一阶环节,时间常数为0.2 s,目标在相对距离小于1 000 m时进行连续机动,过载为nT。脱靶量的计算采用零效脱靶量,在相对距离为100 m时,导弹放弃制导,进行匀速飞行。仿真结果与采用剩余时间和需用过载方法相比较见表3。其中导弹速度为1 000 m/s,目标过载变化及相应的脱靶量如表3所示。可以看到使用模糊规则方法在高速、高机动情况下能够有效的确定直接力引入时机并使得脱靶量减小。本方法是一个在线计算方法,但是在离线确定好模糊规则后,在线进行计算的只有β的清晰化计算,所以总的在线计算量是比较小的,不会增加运算时间。

表3 采用模糊规则方法与常用方法比较

4 结论

文中以应用广泛的比例导引律为基础,针对直接力引入时机问题,提出了一种基于模糊规则的综合设计方法。仿真结果验证了针对不同的导弹速度和目标机动过载情况下,该方法能够有效的确定直接力引入的时机,使得导弹的脱靶量减小。

[1] 闫斌斌, 闫杰. 一种气动力/直接力复合控制导弹的直接力引入时机设计方法 [J]. 弹箭与制导学报, 2007, 27(5): 11-12.

[2] CHADWICK W R. Augmetation of high-altitude maneuver performance of a tail-controlled missile using lateral thrust: ADA 328973 [R]. Virginia: Naval Surface warfare Center, 1995.

[3] 张卫洪, 王青. 基于直接侧向力控制的智能末导引律的设计与仿真 [J]. 战术导弹技术, 2005(4): 36-39.

[4] 王立新. 模糊控制与模糊控制教程 [M]. 王迎军, 译. 北京: 清华大学出版社, 2003: 135-157.

[5] 李志强, 李郝林, 包园园. 一种自适应模糊控制算法 [J]. 精密制造与自动化, 2008(4): 22-23.

[6] 师五喜. 未知多变量非线性系统自适应模糊预测控制 [J]. 控制理论与应用, 2011, 28(10): 1399-1404.

A Design Method of Direct Jet Beginning Time Based on Fuzzy Rules

SONG Guangrun

(No.71315 Unit, Henan Shangqiu 476000, China)

A design method based on fuzzy rules was proposed for solving the problem of searching the beginning time of direct jet in terminal guidance phase. In order to getting the beginning time of direct jet, based on proportional navigation, fuzzy rules were used to synthesize four factors:left time, target maneuver, commanded lateral acceleration and speed of missile. The computer simulation results prove that the method is efficient.

direct jet control; beginning time; fuzzy rules

2016-04-22

宋广润(1985-),男,山东聊城人,硕士,研究方向:精确制导与控制。

TJ765.2

A