任意载弹模式俯仰系统重力矩算法研究

方 航,黄朝学,王敏毅

(中国船舶重工集团公司第710研究所,湖北宜昌 443003)



任意载弹模式俯仰系统重力矩算法研究

方 航,黄朝学,王敏毅

(中国船舶重工集团公司第710研究所,湖北宜昌 443003)

为实时解算某型火箭发射装置俯仰系统重力矩,基于质点系等效质心原理推导出任意载弹模式下重力矩算法模型,采用Matlab编程实现算法并同Pro/E测量计算实际值对比分析。仿真结果表明,该算法满足任意载弹模式下重力矩实时解算要求并达到较高精度,有效解决当前采用Pro/E软件测量并计算重力矩方法工作量大且通用性差等缺点,极大的提高研究效率。

任意载弹模式;火箭发射装置;重力矩;软件算法

0 引言

俯仰系统重力矩大小与载弹模式参数相关,包括高低射角、剩余载弹量、弹种及弹位。当前重力矩主要由平衡机[1]平衡,为设计其结构[2-3]参数,需要获取重力矩负载值作为设计目标,采用Pro/E软件测量俯仰系统重心位置并计算重力矩负载值不仅工作量大且载弹模式改变时需要重新测量计算。

为实时自动解算重力矩负载,必须建立俯仰系统在任意载弹模式下的重力矩算法模型。同当前使用Pro/E软件测量计算固定载弹模式下重力矩方法相比,本算法根据相关传感器采样获取的参数实时解算俯仰系统在任意载弹模式下的重力矩负载,允许工程技术人员实时简便获取俯仰系统的重力矩大小值,极大的减少工作量。

1 重力矩模型算法原理

基于引言分析,假设高低角为θ、剩余载弹量为n、火箭弹种类为s、剩余载弹量分布位置编号为p,重力矩为MG,则必然存在以下函数关系:

MG=f(θ,n,s,p)

(1)

如图1所示俯仰系统由多个质量体组成,包括发射架、火箭弹及附属组部件,各质量体自身质心位置已知。假设系统中有N个质量体,质量均集中于质心处,第i个质量体在全局坐标系中的质心坐标为(xi,yi,zi),其质量为mi,该系统的等效质心记作(xe,ye,ze),根据文献[4]可知系统等效质心满足以下约束条件:

(2)

(3)

(4)

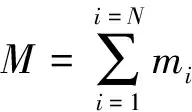
暂且忽略不计。

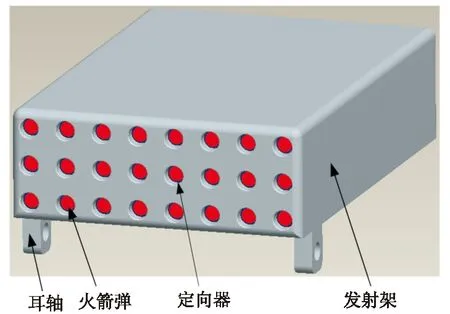
图1 俯仰系统基本组成

2 重力矩模型函数建立

2.1 火箭弹等效质心向量模型

假设以发射架左下角端点建立全局坐标系O0(x0,y0,z0),第i根发射管内火箭弹尾部端面中心建立局部坐标系Oi(xi,yi,zi)并以平行于炮管z0方向为zi轴、平行于x0方向为xi轴、平行于y0方向为yi轴,详见图2、图3所示。在局部坐标系Oi下火箭弹质心记作Gi(xGi,yGi,zGi),x0方向相邻两发射管中心间距为W,y0方向相邻发射管中心间距为H,根据文献[5]求O0坐标系下第i根发射管火箭弹质心向量满足:

O0Gi=(x1+nW+xGi)i+

(y1-mH+yGi)j+(z1+zGi)k

(5)

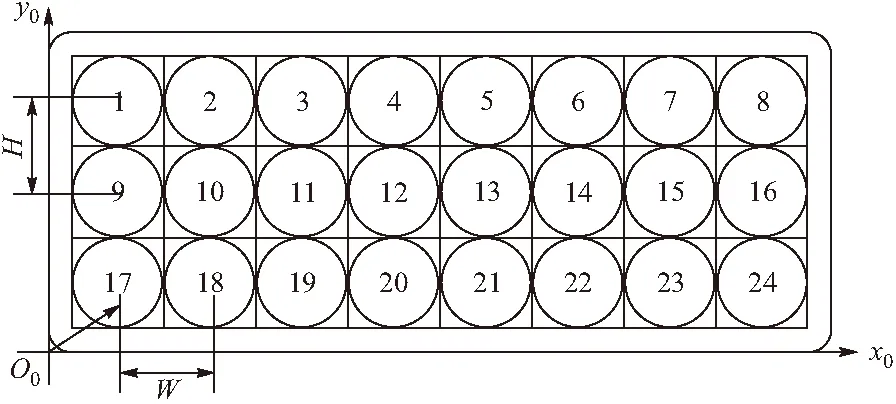
图2 俯仰系统发射管位置编号及全局坐标系

图3 火箭弹1质心及其局部坐标系

假设24根发射管位置视作3行8列矩阵,起始下标均记0,以此类推任意炮管位置编号i记作pi[m][n],建立位置编号pi和对应的数组元素行坐标m、列坐标n之间的函数关系,方便编程及软件实时解算。经理论分析并归纳函数关系如下:

pi=8m+n+1

(6)

定义取整符号[A],表示对数据A舍去小数部分取整数部分,将取整符号用于本模型得:

(7)

(8)

推导出火箭弹全局质心计算公式为:

(9)

2.2 俯仰系统重心坐标计算

假设该火箭发射装置配装弹药为A、B型弹，质量记作mA、mB,某次作战剩余A、B型弹数量为NA、NB枚,第i枚A型弹位置编号为pAi、A型弹在O0坐标系下的质心等效坐标为(XGAi,YGAi,ZGAi),第j枚B型弹位置编号为pBj、B型弹在O0坐标系下的质心坐标为(XGBj,YGBj,ZGBj),A型弹局部质心坐标为(aA,bA,cA),B型弹局部质心坐标为(aB,bB,cB),发射架质量为mf、质心全局坐标为(Xf,Yf,Zf),俯仰系统等效重心坐标记作Oe(Xe,Ye,Ze),i、j为下标索引。依据文献[5],发射装置俯仰系统等效重心坐标计算公式推导如下:

(10)

(11)

(12)

(13)

(14)

(15)

(16)

ZGAi=z1+cA

(17)

ZGBj=z1+cB

(18)

式中0≤NA+NB≤N且为正整数。

2.3 俯仰系统重力矩模型函数

据文献[4],为求解模型函数方便,以两耳轴端面中心点连线中点为原点建立坐标系Or,以耳轴中心线为x轴,平行发射管轴向方向为z轴,垂直x轴、z轴的第三方向为y轴。

OrOe=OrO0+O0Oe

(19)

式中O0Oe为俯仰系统等效质心向量,假设OrO0=-d1i-d2j-d3k,综合式(10)～式(19)可得:

OrOe=(Xe-d1)i+(Ye-d2)j+(Ze-d3)k

(20)

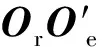
(21)

MG=(mf+NAmA+NBmB)·

(22)

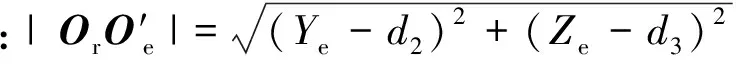
图4 俯仰系统重力矩参数示意图

3 算法实现及仿真计算

3.1 Matlab算法实现

根据重力矩算法编制用户界面GUI如图5所示,算法的Matlab实现代码作为GUI中的控件回调函数。为确保输入A和B两种弹药的位置编号出现重复,软件特设计弹位免重报警功能,如果软件检测到手动输入位置编号重复,则弹位免重报警灯亮(红色),提示用户查检。确认参数无误,单击计算按钮,则该载弹模式下重力矩大小值将显示在结果栏。

3.2 算法仿真计算

为检验该算法正确性及实用性,使用Pro/E软件测量俯仰系统在不同载弹模式下的重心位置,将计算的实际重力矩值同本算法计算的理论结果对比分析。由于俯仰系统载弹模式种类众多,不可能验证所有的工况,特任意选择两种工况作为评估该算法正确性的依据。

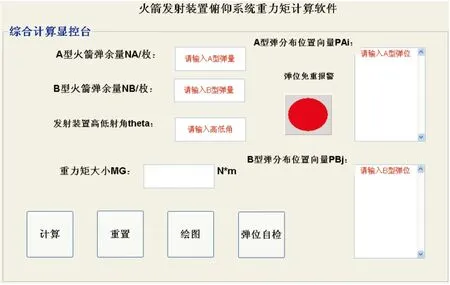
图5 俯仰系统重力矩计算软件GUI

工况1:假定发射管初始配装A型弹24管,高低角θ=0°,每次发射一枚,发射顺序为1,2,3,…,24,理论重力矩记作MGL、实际重力矩记作MGS,工况1的仿真结果如图6～图7所示。

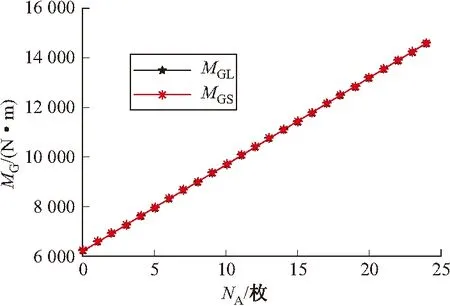
图6 理论与实际重力矩结果对比

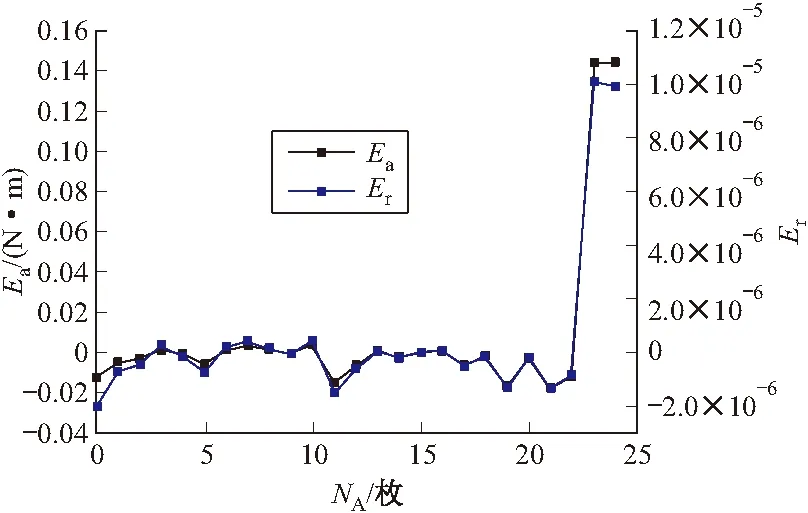
图7 重力矩绝对误差Ea与相对误差Er

结果分析:曲线表明,实际重力矩结果与理论重力矩结果基本吻合(见图6),最大绝对误差Ea,max=0.144 4N·m、最大相对误差Er,max=9.89×10-6<0.1%,工况1下该算法计算结果正确且精度较高,存在极小的误差原因在于载弹模式参数获取存在误差,对理论结果有直接影响。

工况2:假设发射装置初始配装24枚弹药,见表1。

因战术需要发射装置在θ=18°时发射B1、B2、B3共3枚B型弹;

θ=20°时发射B4、B5、B6、B7、 B8共5

枚B型弹;θ=22°时发射B9、B10、B11、B12共4枚B型弹;θ=25°时发射A1、A2、A3、A4、A5、A6共6枚A型弹;θ=35°时发射A7、A8、A9、A10、A11、A12共6枚A型弹,工况2的仿真结果如图8～图9所示。

图8 理论与实际结果对比

图9 重力矩绝对误差Ea与相对误差Er

结果分析:曲线表明,在不同发射角下俯仰系统载弹模式改变时实际重力矩和理论重力矩大小基本一致,最大绝对误差Ea,max=2.228 2N·m、最大相对误差Er,max=0.12%<0.5%,满足精度要求。

4 结论

文中以多管火箭炮武器系统为研究对象,为实时解算俯仰系统重力矩负载值,首先基于质点系等效质心原理推导出任意载弹模式下重力矩算法并采用Matlab编程实现,仿真结果表明:该算法精度高通用性好,解决了传统研究中,使用Pro/E软件测量俯仰系统装配体重心位置,再计算重力矩中工作量大且通用性简便性实时性差等不足。该算法可用于自适应重力矩平衡装置控制系统负载解算单元,对后续俯仰系统自适应平衡装置的研制有积极辅助意义。

[1] 原星武. 某自行导弹防空系统炮塔重力矩平衡技术 [C]∥第九届全国雷达学术年会论文集, 2003: 976-978.

[2] 张鹏, 范树迁, 石明全. 某扭杆式双向平衡机设计及试验分析 [J]. 机械设计与制造, 2011(2): 11-13.

[3] 黄朝学. 某扭杆式双向平衡机的设计及疲劳寿命分析 [J]. 机械设计, 2010, 27(9): 72-75.

[4] 哈尔滨工业大学理论力学教研室. 理论力学 [M]. 7版. 北京: 高等教育出版社, 2009: 28-58.

[5] 同济大学数学系. 高等数学 [M]. 6版. 北京: 高等教育出版社, 2007: 272-282.

[6] 郑文纬, 吴克坚. 机械原理 [M]. 7版. 北京: 高等教育出版社, 1997: 69-76.

[7] 程永强, 韩勇. 某型导弹发射装置平衡机的改装设计 [J]. 军事装备测控技术, 2014, 22(5): 1469-1471.

[8] 方航, 王敏毅, 黄朝学. 某火箭弹发射装置自适应平衡机原理方案研究 [J]. 舰船电子工程, 2015, 35(9): 51-55.

版 权 声 明

凡稿件被本刊录用，即视为作者同意将该论文的复制权、发行权、信息网络传播权、翻译权、汇编权等权利在全世界范围内转让给本刊。本刊已许可中文科技期刊数据库(维普)、万方数据数字化期刊群和中国知网(中国学术期刊(光盘版)电子杂志社)在其各自的系列数据库产品中以数字化方式复制、汇编、发行及在信息网络传播本刊全文。作者著作权使用费和稿酬一并支付(即包括印刷版、光盘版和网络版各种使用方式的报酬)。如作者对本声明持有异议，请在投稿时说明。

本刊编辑部

Study on Gravity Moment Algorithm of Pitch System in Any Loading Mode

FANGHang,HUANGChaoxue,WANGMinyi

(No.710ResearchInstitute,CSIC,HubeiYichang443003,China)

Inordertocalculateloadofgravitymomentofacertaintypeofrocketlauncherinrealtime,basedontheprincipleofequivalentmasscenterofmassofaparticlesystem,themodelfunctionofgravitymomentinanyloadmodewasdeducedandprogrammedwithMatlab,andcomparedwithactualresultsmeasuredandcalculatedbyPro/Esoftware.Simulationresultsshowthatthiskindofalgorithmcansatisfyreal-timesolutionofgravitymomentinanyloadmode,settleseffectivelycurrentuseofPro/Esoftwaretomeasureandcalculategravitymomentmethodwhichhasseriesofshortcomingslikealargeamountofworkandpoorgenerality,whichcangreatlyimproveresearchefficiency.

arbitraryloadingpattern;rocketlauncher;gravitymoment;softwarealgorithm

2015-11-16

方航(1991-),男,湖北黄冈人,硕士研究生,主要研究:动力学与控制、嵌入式系统软硬件设计。

TJ

A