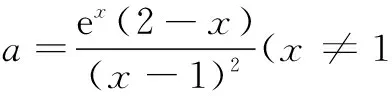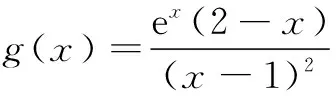例谈参变量的处理方法
孙 浩
(江苏省徐州高级中学,221000)
○学习指导○
例谈参变量的处理方法
孙 浩
(江苏省徐州高级中学,221000)
求参变量取值范围是数学学习过程中常见的一类问题,也一直是高考考查的重点,同时也是教学中的一个难点.下面,举例谈谈笔者对解此类题的方法、思想的归纳.
一、参变量的引入
例1 (2016年江苏高考题)在锐角∆ABC中,若sin A=2sin Bsin C,则tan A·tan Btan C的最小值是______.
分析 本题与苏教版课本必修4第116页例4结论有联系,可用该结论解决问题,也可以引入参变量解决.
解 sin A=sin(B+C)=sin Bcos C+cos Bsin C=2sin Bsin C,两边同除cos B·cos C,得
tan B+tan C=2tan Btan C.
方法1 由课本必修4第116页例4结论有tan Atan Btan C=tan A+tan B+tan C=tan A+2tan Btan C.
在锐角∆ABC中,tan A>0,tan B>0,tan C>0,则
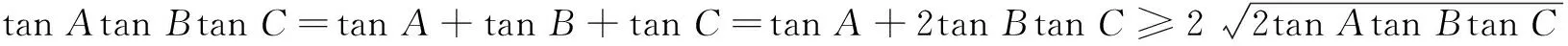
两边平方可求得tan Atan Btan C≥8.
当且仅当tan A=2tan Btan C时,等号成立,即tan Atan Btan C的最小值是8.
方法2 在锐角∆ABC中,由tan B+tan C=2tan Btan C及基本不等式,可证明tan Btan C>1,令tan Btan C=m>1,则
tan B+tan C=2m,
tan Atan Btan C=-tan(B+C)tan Btan C
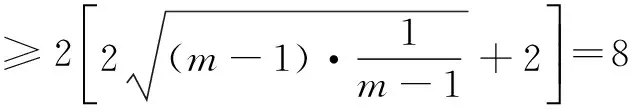
当且仅当m=2时取等号,故tan A·tan Btan C的最小值是8.
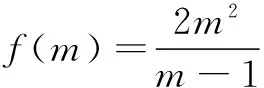
评注 本题少数同学能回归课本结论,用方法1解决,多数学生都是采用了方法2或方法3,引入参数,将三角问题转化为函数求最值问题.可见参数的引入是处理数学问题的常用方法,有助于数学问题的表述及本质的暴露,方便问题的转化.
又如,我们常见到的直线方程问题:在直角坐标系xOy中,过点P(1,2)的直线与x轴,y轴的正半轴分别交于点A、B,求∆ABO的面积最小值,以及此时所对应的直线方程.在解答时,可以设成点斜式,引入斜率参数;可以设成截距式,引入截距参数;可以利用三角函数解决,引入角度参数.通过引入参变量,将题目化归为熟悉的数学问题加以解决.
二、参变量的消去
消元法是解题的通法,代入消元,加减消元,都可以起到化多为少,化繁为简的作用.
例2 已知x,y>0,x+y=1,求证:

分析 可采用消元法构造函数,转化为求函数值域的问题.
解 依题意,y=1-x(0 ∴(x+1)2+(y+1)2=2x2-2x+5. 令f(x)=2x2-2x+5. 例3 已知2sin 2x=sin θ+cos θ,sin2x=sin θcos θ,求cos 2x的值. 分析 本题中出现两个变量,根据问题要求可以确定x为“主元”,通过三角函数恒等变形消去参数θ. 解 由2sin 2x=sin θ+cos θ两边平方,可得 4sin22x=1+2sin θcos θ=1+2sin2x, 即 4(1-cos22x)=2-cos 2x, 整理得4cos22x-cos 2x-2=0, 又cos 2x=1-2sin2x=1-2sin θcos θ=(sin θ-cos θ)2≥0,所以 例4 (2016年浙江高考题)已知平面向量a,b满足|a|=1,|b|=2,a·b=1,若e为平面单位向量,则|a·e|+|b·e|的最大值是______. 分析 设平面单位向量e=(cos θ,sin θ),这里隐含了消元的思想. 设e=(cos θ,sin θ),则 |a·e|+|b·e| 例5 (2012年江苏高考题)已知正数a,b,c,满足: 分析 由本题的结构看,容易联想到借助于线性规划知识来解决.但三个未知数又让我们很难入手解决,能不能简化为我们熟悉的两个未知数是解题关键. 评注 本题首先通过比值换元,把三元问题转化为二元问题,借助于导数、线性规划的知识来解决.本题对能力要求高,需要灵活运用导数、线性规划等数学知识. 在不等式证明中应用换元,能简化证明过程,尤其对含有若干个变元的齐次轮换式或轮换对称式,通过换元变换形式,往往能够事半功倍. 比如:已知a,b,c>0且互不相等,求证: 即只要证不等式 x2+y2+y2>xy+yz+zx. 由基本不等式易证此不等式成立. 例6 (2016年江苏高考题) (1)求方程f(x)=2的根; (2)若对于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值. f(x)=2x+2-x. (1)方程f(x)=2即2x+2-x=2,即(2x)2-2·2x+1=0,所以(2x-1)2=0,于是2x=1,解得x=0. (2)由条件,知 f(2x)=22x+2-2x=(2x+2-x)2-2 =(f(x))2-2. 因为f(2x)≥mf(x)-6对于x∈R恒成立,且f(x)≥2,所以 对于x∈R恒成立. =4. 当f(x)=2,即x=0时取等号,所以m≤4,故实数m的最大值为4. 评注 在高考考题中常常涉及求参变量取值范围问题,这类问题常采用参变量分离的方法来解决,先分离出参变量m,然后转化为求最值或值域. 例7 (2016年全国高考题) 已知函数f(x)=(x-2)ex+a(x-1)2有两个零点,求a的取值范围. 解 由f(x)=(x-2)ex+a(x-1)2=0,得 当x∈(-∞,1)时,g′(x)>0,g(x)在(-∞,1)内单调递增,当x→-∞时,g(x)→0;当x→1时,g(x)→+∞,故g(x)在(-∞,1)内的值域为(0,+∞). 当x∈(1,+∞)时,g′(x)<0,g(x)在(1,+∞)单调递减,当x→1时,g(x)→+∞;当x→+∞时,g(x)→-∞,故g(x)在(1,+∞)内的值域为(-∞,+∞). 所以f(x)有两个零点,即a=g(x)有两个实根,则a的取值范围为(0,+∞). 评注 参变量的分离免去了对参数的讨论,相比较分类讨论显得直截了当.对分离后的函数g(x)的研究用到了简单的极限分析,虽是高等数学所涉及的内容,但能帮助我们快速把握图象的变化趋势,对解题很有帮助. 对于参变量的处理方法,需要我们在分析问题和解决问题的过程中去思考、感悟、把握,不断反思参变量引入、消去、转换、分离的合理性、简洁性、有效性,体会“设元、消元、分离”的解题功能.

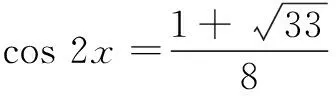

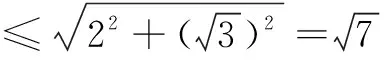
三、参变量的转换
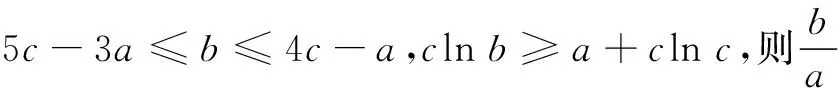




四、参变量的分离