直线与圆中两个关联问题的探究

金卫国

(江苏省海安高级中学，226600)



直线与圆中两个关联问题的探究

金卫国

(江苏省海安高级中学，226600)

事物是普遍联系的,数学知识、数学问题的关联性更能反映这一点.在苏教版数学必修2“直线与圆”的教学过程中,笔者发现有两个比较有趣的关联问题.现整理如下，以飨读者.

问题1 (1)已知点P(x0,y0)为圆C:(x-a)2+(y-b)2=r2(r>0)上一点,求过点P的圆C的切线方程;

(2)已知点P(x0,y0)为圆C:(x-a)2+(y-b)2=r2(r>0)外一点,过点P的圆C的两条切线,切点分别为A、B,求直线AB的方程(即“切点弦”方程).

上述两个小问题,条件和结论有明显的不同,但是通过求解会发现,两者的结果居然相同,都是(x0-a)(x-a)+(y0-b)(y-b)=r2,而且结构与“圆的标准方程”神似!这是偶然还是必然?它们两者之间有联系吗?如果有,有怎样的联系?我们不妨通过求解这两个问题的过程挖掘其中的关联性.

对于(1)，设点Q(x,y)为切线l上任意一点.

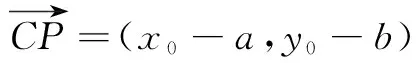
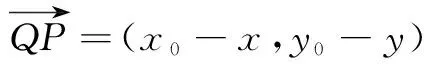
所以有

(x0-a)(x0-x)+(y0-b)(y0-y)

=0；

①

又 (x0-a)2+(y0-b)2=r2.

②

②-①，得

(x0-a)(x-a)+(y0-b)(y-b)=r2.

当点Q与点P重合时,则Q(x0,y0)代入上式,显然成立,

故所求的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.

对于(2)，解决此问题的方法较多,通常有如下三种方法：

方法1 可先求出以线段CP为直径的圆M的方程,与圆C的方程联立,相减即得;

方法2 也可先求出以P为圆心,线段PA为半径的圆N的方程, 与圆C的方程联立,相减即得;

方法3 分别求出切线AP、BP的方程,分别与圆C联立方程组之后求出切点A、B的坐标,进而求出直线AB的方程.

显然,上述方法3最容易想到,但运算量一般较大,方法1和方法2简便一些,但也有些繁琐.下面介绍第4种解法:

设切点A(x1,y1),B(x2,y2).由(1)的结论知,过点A的圆C的切线方程l1为

(x1-a)(x-a)+(y1-b)(y-b)=r2;

过点B的圆C的切线方程l2为

(x2-a)(x-a)+(y2-b)(y-b)=r2.

而直线l1,l2均过点P(x0,y0),所以有

(x1-a)(x0-a)+(y1-b)(y0-b)

=r2；

③

(x2-a)(x0-a)+(y2-b)(y0-b)

=r2.

④

由③ ④ 两式知A(x1,y1),B(x2,y2)均满足直线方程

(x-a)(x0-a)+(y-b)(y0-b)=r2.

由于过两点A、B的直线有且仅有一条,所以所求的直线方程即为

(x-a)(x0-a)+(y-b)(y0-b)=r2.

由上面的求解过程可以看出,(2)的解答过程用了(1)的结论,且(2)的解答过程中充分运用了③ ④ 两个方程结构上的对称性进行了巧妙的替换,使得问题(2)的解答既方便简捷又在整个过程中没有“破坏”方程的原始结构.

从“运动”、“极限”的角度可以把点P看作一个动点,当点P从圆C外向圆C逐渐靠拢时,两切点A,B也逐渐靠拢；当点P运动到圆C上时,两切点A,B就重合于点P.这时的直线AB就相当于过点P的圆C的切线了,从而问题(1)就相当于问题(2)的特殊情形.

综上所述,这两个看似不同问题而答案相同的疑惑也就解决了.

问题2 已知圆C1:x2+y2+D1x+E1y+F1=0;圆C2:x2+y2+D2x+E2y+F2=0.(注:两圆圆心不同)

(1)若两圆相交于A,B两点,求直线AB的方程(即公共弦方程);

(2)若两圆外切,(1)中求得的方程表示什么?外离、内切、内含呢?

这个关联问题中的(1)和(2)又有什么联系呢?

对于(1)，设交点A(x1,y1),B(x2,y2),则

两式相减，得

(D1-D2)x1+(E1-E2)y1+F1-F2

=0；

⑤

同理有

(D1-D2)x2+(E1-E2)y2+F1-F2

=0.

⑥

由⑤ ⑥ 两方程知，点A(x1,y1),B(x2,y2)同时满足方程

(D1-D2)x+(E1-E2)y+F1-F2

=0.

⑦

因为两圆的圆心不同,上式中的D1-D2与E1-E2不可能同时为0,所以方程⑦ 表示一条直线,从而直线AB的方程即为(D1-D2)x+(E1-E2)y+F1-F2=0.

对于(2)，若两圆外切或内切,我们可以运用探究上一个关联问题中的“运动”与“极限”观念：两圆的切点相当于两个交点A,B无限靠近而成的一个点,这时的直线AB就相当于过切点的两圆的内公切线了.但是,我们可以发现,当两圆外离或内含时,上面的方程⑦ 依然存在,显然不表示公共弦所在直线或公切线,这条方程所表示的直线此时似乎是“虚无”的,果真如此吗?

我们不妨从两圆外切的情况来探究.如图1,设直线l是经过点公切点A的一条公切线,点P是直线l上的任意一点(除点A外).过点P 作两圆的切线,切点分别为C,D,这时容易得到PC=PA=PD,从而我们有如下结论:

结论 在方程(D1-D2)x+(E1-E2)y+F1-F2=0所表示的直线l上任意取一点P(该点在两圆外).过点P作两圆的切线,则这些切线长相等.(这里的切线长相等也叫“幂相等”)

上述结论对于两圆内切的情形，同理可得.

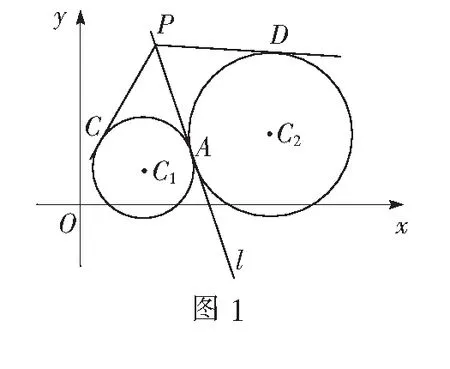
上述结论对于两圆外离和内含的情形也同样成立吗?探究如下:

设圆心C1(a,b),C2(m,n),直线l上一点P(x,y)(点P在两圆外),圆C1,圆C2的半径分别为r1,r2,则

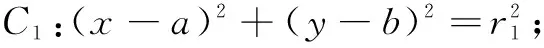
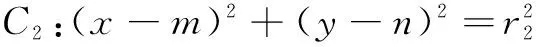
比较系数得

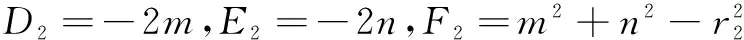
所以由

两式相减，得PC2-PD2=(D1-D2)x+(E1-E2)y+F1-F2.

因为点P(x,y)在直线l:(D1-D2)x+(E1-E2)y+F1-F2=0上,

所以PC2-PD2=0,即PC=PD，从而上述结论成立.

以上探究过程并没有限定两圆的位置关系,所以对于圆与圆的5种位置关系,上述结论都是成立的.方程⑦ 所表示的直线并不是“虚无的”、没有意义的；相反,这条直线是任意两个圆心不同的圆的共同性质,更具有普遍性,这条直线我们通常把它叫做“等轴线”.

通过以上一个关联问题的探究,可以看出诸多事物之间看似“矛盾”或“不相干”,但实际上又是普遍联系、和谐统一的.在探究这两个关联问题的过程中,笔者也注意了求解方法的简洁性、书写结构的对称性,这些都是数学中的美.在平时的数学学习中,我们只要细心留意,数学的美就会不断地被我们发现,并且能为我所用,让我们感觉到学好数学是一件轻松愉快的事!