一道课本习题的启发
翟爱国
(江苏省兴化市戴南高级中学,225721)
一道课本习题的启发
翟爱国
(江苏省兴化市戴南高级中学,225721)
课本习题 (《普通高中课程标准实验教科书》必修2第88页“探究·拓展”15)已知两条直线a1x+b1y+1=0和a2x+b2y+1=0都过点A(1,2),求过两点P1(a1,b1),P2(a2,b2)的直线的方程.
解 因为直线a1x+b1y+1=0,a2x+b2y+1=0都过点A(1,2),所以a1+2b1+1=0,a2+2b2+1=0.由于P1(a1,b1),P2(a2,b2)均适合方程x+2y+1=0,且两点确定一条直线,所以所求直线的方程为x+2y+1=0.
点评 等式a1+2b1+1=0和a2+2b2+1=0是直线a1x+b1y+1=0和a2x+b2y+1=0都过点A(1,2)的代数表示.由a1+2b1+1=0和a2+2b2+1=0得到过两点P1(a1,b1),P2(a2,b2)的直线的方程x+2y+1=0,此为上面两个代数表达式赋予点在直线上的几何意义.这种几何图形的运用在数学中所具有的最大优势就是直观易懂,能解决相关不易求解的代数问题.若本题把问题所求改成“求过两点P1(a1,2b1),P2(a2,2b2)的直线的方程”,学生很容易写出所求直线的方程为x+y+1=0.


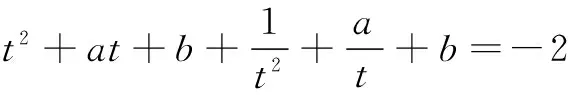

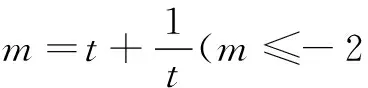
m2+am+2b=0.
设点P(a,2b),则点P(a,2b)在直线mx+y+m2=0上,a2+4b2为点P(a,2b)到定点O(0,0)的距离的平方.从而

等号当且仅当m=±2,即t=±1时成立.

比如,解方程组
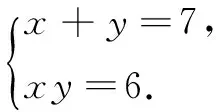
根据一元二次方程根与系数的关系,把x、y看成是方程z2-7z+6=0的两根,解方程得z=1或z=6.从而原方程组的解是
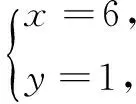
解 联立方程组
消去y,解得x=-4或x=0.
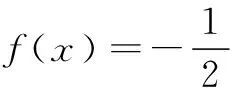

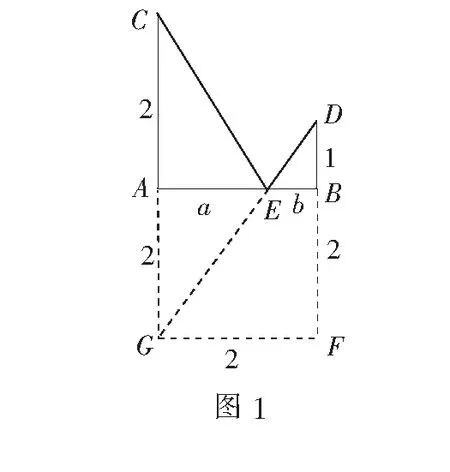
分析 由求解式子的特点可以联想到构造直角三角形利用勾股定理进行处理.
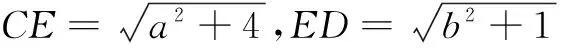
下面求解DG.延长DB至点F,使BF=AG,连结GF,此时构出一个Rt∆DGF,在这个直角三角形中,有

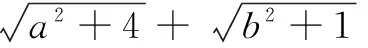
在代数问题中,直观运用几何图形常常体现在利用数轴及平面直角坐标系将一些代数表达式赋予几何意义,通过构造几何图形,进而帮助求解相关代数问题,或者简化相关代数运算.几何直观能力的培养有利于学生理解和解决数学问题,有助于学生发展思维能力和创新能力.随着新课程理念不断深入,几何直观能力的教育价值也日益提升,如何培养学生几何直观能力也成为数学教育中的一个热点问题.
综上所述,几何直观值得我们给予足够的重视,它有助于提高学生分析问题和解决问题的能力.在数学教学与学习中借助几何直观进行解题的例子不在少数,几何直观不仅仅是一种解题方法,几何直观更是一种能力或意识,它的培养是一个漫长的过程.教师要在平时教学过程中不断渗透和总结,让这种意识常伴学生左右,让学生在理解和运用中不断提升自身的几何直观能力,最终促进学生发展.

