浅议基础薄弱生数学素养的培养
——以一道高考题解法与引申为例
林廷胜
(福建省三明市大田县第五中学,366100)
浅议基础薄弱生数学素养的培养
——以一道高考题解法与引申为例
林廷胜
(福建省三明市大田县第五中学,366100)
高中数学基础薄弱生,顾名思义这类学生由于数学基础薄弱,以致在学习数学过程中会有种种学习的障碍.这就要求我们老师在教学过程中,应充分了解学生的学情,认真备课,准确预见学生学习过程的学习障碍,及时进行补缺补漏,扫清学生学习道路的障碍.重视数学基础薄弱生数学基础知识的同时,我们也要重视其数学素养的培养,其中,数学的解题是数学素养培养的重要途径.解题教学并非仅限于得到题目的答案,更重要的是通过解题培养学生提出问题、分析问题、解决问题的能力.本文对2016年高考理科数学北京卷第19题的解法作了探讨及引申,以企抛砖引玉.
(1)求椭圆C的方程;
(2)设P是椭圆C上一点,直线PA与y轴交于点M, 直线PB与x轴交于点N,求证:|AN||BM|为定值.
以下仅对第(2)问的解法进行探讨并对问题作进一步引申.
一、一题多解
一题多解有利于增强学生的分析问题、探索问题与解决问题的能力,有利于拓展学生思维的广度与培养学生思维的创造性.
本题中要证明|AN||BM|为定值,可以先从点P取特殊位置开始(如点P在下顶点或左顶点).了解了定值是4,接下来只要证明点P在一般位置时定值都为4即可.
分析1 讨论直线BP斜率不存在与存在.斜率存在可设直线BP方程为y=kx+1,|AN|与点P坐标由k的代数式表示,得到直线AP方程,|BM|由k的代数式表示,最后得到|AN||BM|=4.
解法1 当直线BP斜率不存在时,点N即为原点O(0,0),点M为椭圆的下顶点|AN|=|BM|=2,|AN||BM|=4.
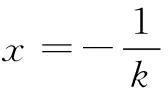
直线AP的方程为


分析2 可设直线AP方程为y=k(x-2),|BM|与点P坐标由k的代数式表示,得到直线BP方程,|AN|由k的代数式表示,最后得到|AN||BM|=4.
解法2 直线AP的斜率存在,设直线AP的方程为y=k(x-2),令x=0,则y=-2k,即M(0,-2k),|BM|=|2k+1|.
直线BP的方程为


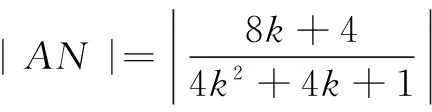
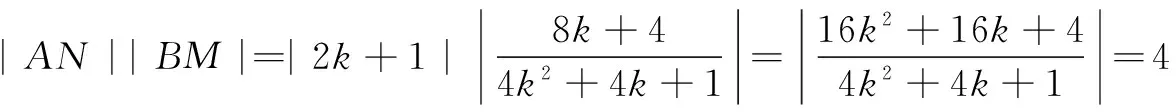
分析3 讨论直线AP斜率为0与不为0.斜率不为0时,可设直线BP方程为x=ty+2.
|BM|与点P坐标由t的代数式表示,得到直线BP方程,|AN|由t的代数式表示,最后得到|AN||BM|=4.
解法3 当直线AP斜率为0时,点N即左顶点(-2,0),点M为椭圆的为原点O(0,0),|AN|=4,|BM|=1,则|AN||BM|=4.


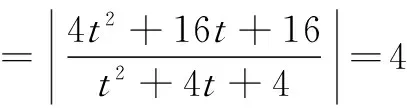
分析4 设P(x1,y1),则直线AP、BP方程由x1、y1表示,进而M、N坐标x1、y1表示,|AN|与|BM|由x1、y1表示,最后得到|AN||BM|=4.
解法4 设P(x1,y1),则直线AP方程为

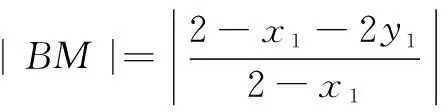

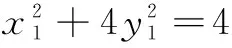
|AN||BM|
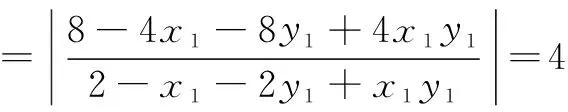
分析5 利用椭圆的参数方程可设P(2cos α,sin α),则直线AP、BP方程由2cos α、sin α表示,进而M、N坐标2cos α、sin α表示,|AN|与|BM|由2cos α、sin α表示,最后得到|AN||BM|=4.

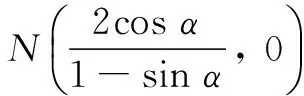
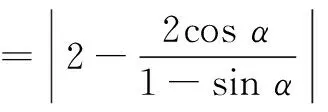

二、结论引申
引申是指根据题目的条件、结论,挖掘题目条件与结论内在的联系与规律,进而推广到具有一般性的结论.引申有利于培养学生探索精神,培养学生发现问题、解决问题的能力,有利于挖掘学生思维的深度与加强学生思维的深刻性.

证明 设P(x1,y1),则直线AP方程为


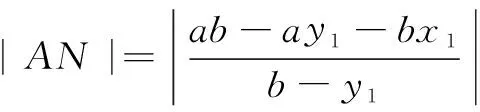
因为P(x1,y1)在椭圆上,则

|AN||BM|
=2ab(定值).
通过对高考题的解法探讨与引申有利于激发学生学习数学的兴趣,拓展学生思维的广度与培养学生思维的创造性,有利于挖掘学生思维的深度与加强学生思维的深刻性,充分体现《标准》的要求.在教学过程中注重培养学生数学地提出问题、分析问题和解决问题的能力,发展学生的创新意识和应用意识,提高学生数学探究能力、数学建模能力和数学交流能力.
(本文系福建省教育科学“十二五”规划2015年度立项课题(FJJK-550:农村高中数学基础薄弱生的课堂教学方法研究)研究成果)

