例说向量题的求解策略

陈建叶

(江苏省苏州市吴江中学,215200)



例说向量题的求解策略

陈建叶

(江苏省苏州市吴江中学,215200)

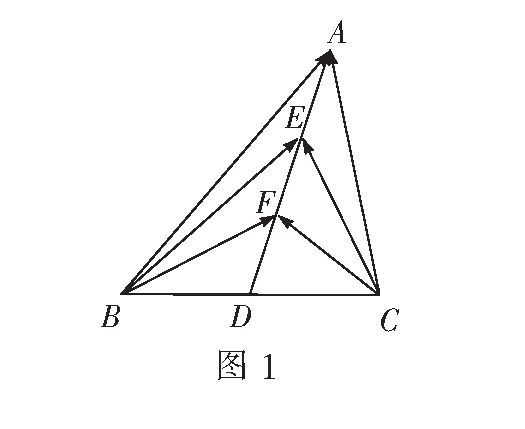
平面向量是数和形联系的纽带,它既有数的相关运算,又有形的结构特点,具有代数与几何的双重身份,在高考命题中受命题者青睐.这类问题往往条件不多,比较简练,注重对学生思维能力的考查,难度较大,学生对于它往往感到无从入手.本题是2016年江苏高考数学填空题第13题，该题以向量的数量积计算为命题背景,考查了三角形的中点性质、基底思想、坐标化思想等，这些经典的性质与思想方法充分反映了向量题的解题策略.本文就以该题为例,谈一谈平面向量问题解决的策略,供大家参考.

策略1 基底意识,转化与化归思想

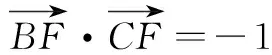
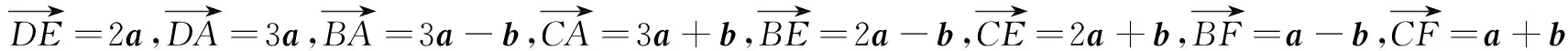
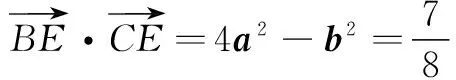
策略2 坐标意识,方程思想的运用

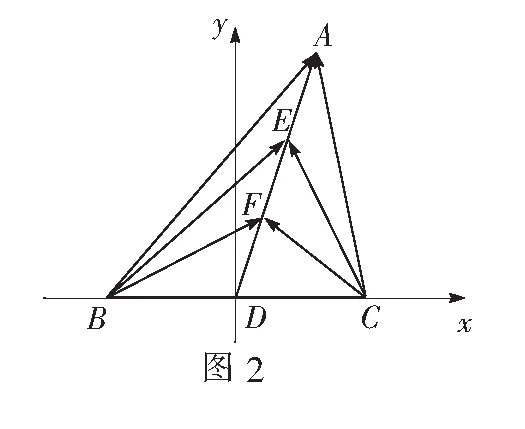
解法3 如图2,以BC为x轴,BC的中点D为坐标原点,建立直角坐标系,设B(-a,0),C(a,0),A(b,c),则

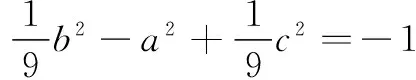
即 b2-9a2+c2=-9.

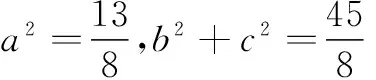
策略3 特殊化意识,一般到特殊思想

特殊化,即借助特殊情形获取结论,这是解决填空题的一种常用且简捷的方法,但前提是可以断定结论是确定的,力求小题小做.本题由题意,其结论为定值,可以用特殊模型来借助等腰三角形求解.

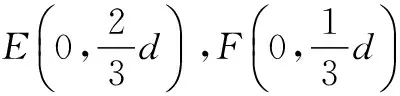
策略4 几何意识,中点向量性质的运用

向量具有明确的几何意义, 对于涉及中线的向量问题,一般利用向量加、减法的平行四边形法则进行求解,这也是解决向量问题的常用方法之一.

又E,F是AD上的两个三等分点,上式即

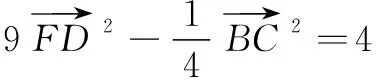
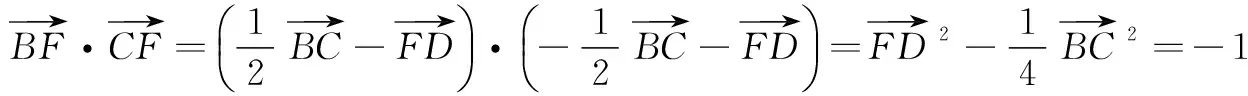
总之,向量数量关系的运算,已逐渐成为高考考查向量试题中的一个热点.它的考查方式多种多样,无论如何多变,我们应该抓住高考题中的一些典型题目进行研究、归纳，总结解题方法,归纳数学思想,跳出题海战术,真正减轻学生的负担,提高学生的解题能力.