破解数量积之四宝

浙江省诸暨市浬浦中学(311824)

王苏文●



破解数量积之四宝

浙江省诸暨市浬浦中学(311824)

王苏文●

平面向量既是代数的对象，又是几何的对象，作为代数对象，可以进行运算；作为几何对象，可以刻画线、面等几何对象.向量集数形于一身，是沟通代数与几何的天然桥梁.数量积不但有简单的代数运算，而且具有一定的几何意义，因此破解数量积问题主要从数、形两条主线展开.本文列举两条主线下的其中四宝，与大家一起商讨.

一宝：坐标法

当遇到所求向量难以看清，但与已知向量存在某种关系，加之已知向量的夹角与长度确定时，可借助坐标系进行坐标处理.

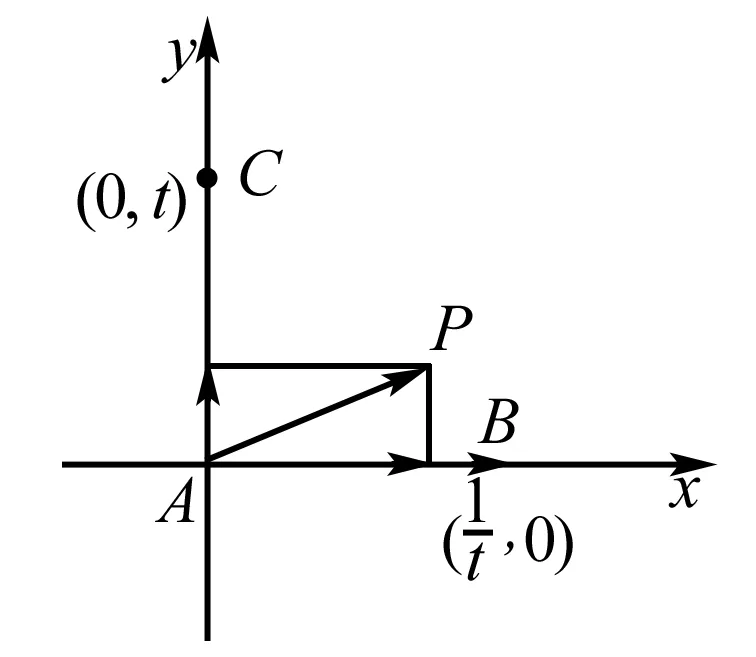
A．13 B．15 C．19 D．21

解析 根据题意，建立以A为坐标原点的平面直角

因为t∈[0,1],所以f(t)递减,

点评 通过建立坐标系，将向量数量积运算，转化为坐标运算，最终转化成函数问题.

二宝：基底法

当题中所有向量都与某两个向量有关，可利用这两个向量为基底，建立相关关系.

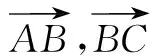
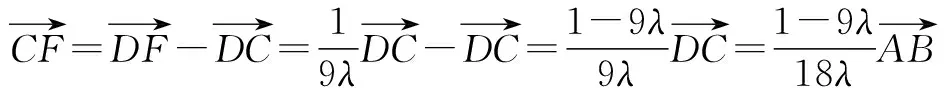
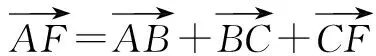
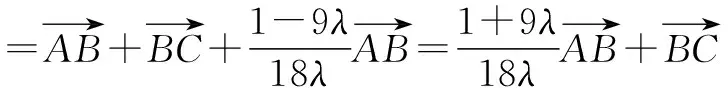
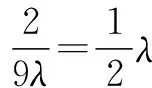
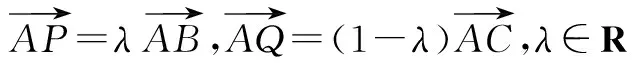
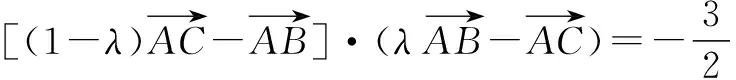
故4λ+2(λ2-λ-1)+4(1-λ)=3/2,解得λ=1/2.

点评 通过基底将所有向量转化为两个向量间的运算，实现统一性.

三宝：几何意义

遇到一些与垂直有关的数量积运算，可借助数量积的几何意义进行求解.

A.-8B.-1C.1D.8

分析 由于本题涉及到圆的问题，圆中的弦联想到垂径定理.

点评 充分利用数量积的几何意义将数量积运算表现得淋漓尽致.

四宝：向量恒等式

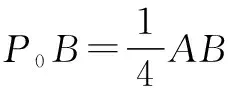
A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

分析 对于学生而言难度还是有的，很多学生认为此题是选择题中最难的一题，很多有关本题的相关解法都已发表在各种杂志上，但总的来看，用上述恒等式来处理本题还是显得更为巧妙.

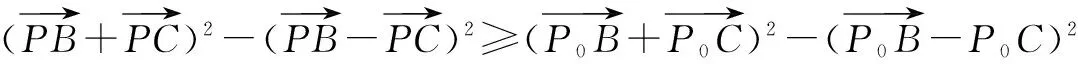
点评 本题应用定点E与线段AB上的动点P的最小值为P0E，即垂线段最短，因此P0E⊥AB，结合E,P0为BC,BF的中点，故FC⊥AB，从中将恒等式在本题中表现得更加淋漓尽致.

G632

B

1008-0333(2016)22-0018-02