用Mathematica分析电磁感应类问题的自洽性
陆天明
(南京师范大学附属中学江宁分校,江苏 南京 211102)
用Mathematica分析电磁感应类问题的自洽性
陆天明①
(南京师范大学附属中学江宁分校,江苏 南京 211102)
对电磁感应类问题的自洽性进行分析时,一般会碰到超越方程和微分方程,处理这些方程是一件费时耗力的事,如利用Mathematica软件,则分析过程会显得非常简单.Mathematica不仅可以进行符号运算,得到解析解,对于一些无法得到解析解的方程,也会给出令人满意的数值解.
Mathematica;电磁感应;自洽性
电磁感应类问题常常有着比较强的综合性,可以很好地考察学生的知识水平和分析解决问题的能力,一直受到命题者的青睐.但这类问题所涉及的运动过程一般较为复杂,对数学的要求常会超出学生的现有水平,命题者为了使题目能够被高中学生解决,一般会直接或间接给定物理量的数值,这很容易导致题目的科学性错误,造成不自洽的问题.所以,在日常教学过程中,常要考察这类题目的自洽性,这时就会碰到超越方程和微分方程,处理这些方程是一件十分费时耗力的事,若能借助Mathematica软件,则会使工作效率大大提高.Mathematica是美国物理学家Stephen Wolfram设计开发的一款优秀的科学计算软件,可以进行复杂的符号运算、数值运算和图像处理,功能非常强大.下面就用Mathematica来分析两道典型的电磁感应问题的自洽性.

图1
如图1所示,在粗糙绝缘水平面上有一正方形闭合金属线框abcd,其边长为l=1m、质量为m=2kg、电阻R=1Ω.金属线框与水平面的动摩擦因数μ=0.8.边界右侧有一足够大的匀强磁场区域,磁场方向竖直向下,磁感应强度B=2T.开始时金属线框的cd边与磁场的边重合,现使金属线框以初速度v0=10m/s沿水平面进入磁场区域,线框完全滑入磁场区域后又滑行l距离后停下,求金属线框进入匀强磁场所经历的时间t.

在图1中以边界上取一点为原点,垂直于边界建立x轴.


可以看到,用Mathematica求解微分方程显得很简洁,特别是在用Mathematica求解线框第1阶段运动的未速度的具体数值时,涉及的方程是超越方程,凭借纸笔运算是非常困难的,而这里用Mathematica来处理,显得非常简单.
再来研究一道更加复杂的自洽性问题,如图2所示,质量为m、电阻为R的单匝矩形线框置于光滑水平面上,线框边长ab=L、ad=2L.虚线MN过ad、bc边中点.一根能承受最大拉力F0的细线沿水平方向拴住ab边中点O.从某时刻起,在MN右侧加一方向竖直向下的匀强磁场,磁感应强度大小按B=kt的规律均匀变化.一段时间后,细线被拉断,线框向左运动,ab边穿出磁场时的速度为v.求:
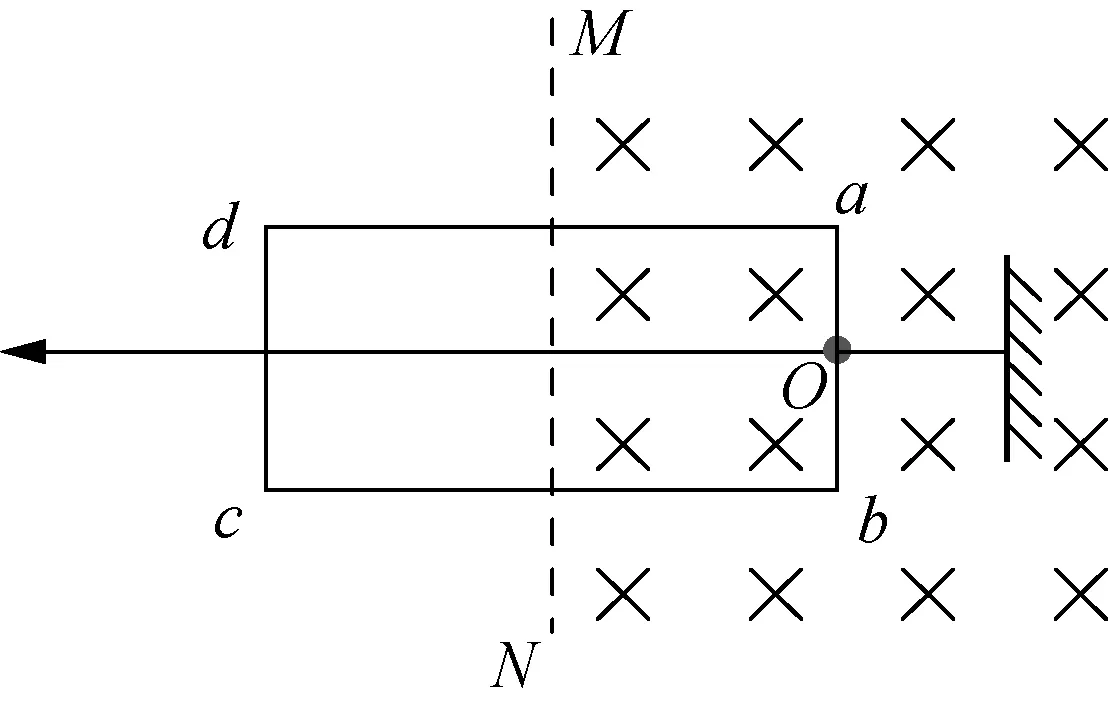
图2
(1) 细线断裂前线框中的电功率P;
(2) 细线断裂后瞬间线框的加速度大小a及线框离开磁场的过程中安培力所做的功W;
(3) 线框穿出磁场过程中通过导线截面的电量q.
命题者似乎已经感觉到了这类问题会出现自洽性问题,所以没有给出各物理量的具体数值,但仔细分后还是发现了存在自洽性问题.
在图2中建立坐标系,以O点为原点,水平向左为正方向.

Clear["Global`*"]
F0=10;L=1;k=1;m=0.2;R=1;t0=F0*R/(L^3*k^2);tt=100*t0;
a=L^2*k^2/(m*R);
ode1={x''[t]+a*t^2*x'[t]+a*t*x[t]-a*L*t==0,x'[t0]==0,x[t0]==0};
A1=NDSolve[ode1,x,{t,t0,tt}]
x=First[x/.A1](*得到插值函数*);
x[tt](*求末时刻线框的位置*)
x'[tt](*求时刻线框的速度*)
x''[t0](*求线框开始运动时的加速度*)
Plot[x[t],{t,t0,tt},Axes->True,PlotRange->{{t0,tt},{0,2}}](*作出位移-时间图像*)
Plot[x'[t],{t,t0,tt},Axes->True,PlotRange->{{t0,tt},{0,0.2}}](*作出速度-时间图像*)
运行上述程序可以得到:线框开始运动时的加速度为a=50m/s2,可以求出线框的末位置为:9.89999×10-1<1m,末速度为v=1.0005×10-5m/s.代入不同数值进行验证,均得到线框没有离开磁场区域,即原题不自洽,程序给出的位移-时间图像如图3,速度-时间图像如图4.

图3

图4
由以上两例可以看到,Mathematica在验证电磁感应类问题的自洽性时显得特别有力.实际上,中学物理中有很多问题都可以运用Mathematica来处理,不仅可以用来求解各种方程和绘制图像,还可以用来模拟物理过程,处理实验数据等.Mathematica功能非常强大,应用极其广泛,而且简单、易学、操作方便,是一款值得深入研究的软件.
褚小坤.电磁感应问题的自洽性探讨[J].物理之友,2016,32(7).
①名师简介:陆天明(1969— ),男,江苏南京人,南京师范大学附属中学江宁分校教研部副主任,《物理之友》编委,南京市物理学科带头人,南京物理学会理事,南京师范大学物理教育研究所兼职研究员,研究方向为物理课程与教学论.

