粗粒土静止侧压力系数试验

朱俊高,蒋明杰,沈靠山,褚福永

(1. 河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098; 2.河海大学岩土工程研究所,江苏 南京 210098;3. 浙江省钱塘江管理局勘测设计院,浙江 杭州 310016; 4. 丽水学院土木工程学系,浙江 丽水 323000)



粗粒土静止侧压力系数试验

朱俊高1,2,蒋明杰1,2,沈靠山3,褚福永4

(1. 河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098; 2.河海大学岩土工程研究所,江苏 南京 210098;3. 浙江省钱塘江管理局勘测设计院,浙江 杭州 310016; 4. 丽水学院土木工程学系,浙江 丽水 323000)

对某土石坝地基覆盖层2种级配的砂卵砾石料进行大型单向压缩试验,试验中,土压力盒基于标定方法提供的参数得到试样内的水平应力和垂直应力,进而计算其静止侧压力系数K0。研究水标法和砂标法对粗粒土的适用程度,探讨K0试验结果的可靠性;分别对2种级配土料进行中三轴CD试验,测定土料的有效内摩擦角,然后依据相关经验公式计算K0,验证经验公式的有效性。结果表明:砂标法对于粗粒土来说是一种较可靠的标定方法;在竖向应力足够大时,K0试验误差可以忽略不计,所测定的K0接近实际值；Federico基于Terzaghi的已激发有效摩擦角概念而推导出的有效内摩擦角与静止侧压力系数之间的关系式较适合粗粒土。

粗粒土;静止侧压力系数;大型单向压缩试验;土压力盒;有效内摩擦角;已激发有效摩擦角

土石坝具有对地质条件要求低、抗震性能强、经济效益好等优点,常常作为在深厚覆盖层上筑坝的优选坝型[1]。在土石坝数值计算中,要准确计算坝体和地基中防渗墙的应力变形,地基的初始状态比较重要,如果能准确评估,无疑会提高计算精度。在深厚覆盖层上筑坝,筑坝前覆盖层已处于固结稳定状态,后期的坝体填筑以及蓄水荷载可近似认为是静止侧压力系数K0固结条件下的加载,同时,山区河流的地基覆盖层常常是粗粒土,因此,合理确定粗粒土的K0比较重要,值得深入研究。

目前,K0的确定方法有直接和间接2种方式。所谓直接方式是指通过现场试验或者室内试验直接测量无侧向变形土体的竖向应力和侧向土压力,从而计算土体的K0。室内直接方式测K0比较常用的方法是压缩仪法和三轴仪法。另外,不少学者提出了一些新的试验方法,如Garga 等[2]提出了一种用应力路径三轴仪确定严重超固结黏土的静止侧压力系数的室内试验方法;Chen 等[3]研制了用于量测静止侧压力系数的大型土压力模型试验设备。间接方式通常是依据强度试验结果如土体有效内摩擦角,利用经验公式计算K0。当然,经验公式的提出要基于大量的试验资料。如Jaky[4]在1948年推导了有效内摩擦角(以下简称摩擦角)φ′和静止侧压力系数K0的关系式:

(1)

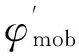
(2)

式(2)中已激发角虽然无法直接计算,但能由土体内摩擦角推导而得。关于已激发角与内摩擦角之间的关系,许多学者进行了研究,其中Abdelhamid等[6]基于Rowe的假设认为黏土适用于下式：

(3)

通过研究文献及相关试验结果,Hayat[7]得到黏土适用以下关系式:

(4)

Simpson[8]通过BRICK模型推得黏土适用于:

(5)

Federico等[9]对一系列实测静止侧压力进行统计分析,推得了压缩性黏土适用如下关系式：

(6)

虽然有不少学者对K0的试验和估算方法做过很多有价值的探索[10-13],但是他们绝大多数都是针对砂土或黏土的,较少涉及粗粒土。现有的试验方法中,常用的压缩仪法和三轴仪法均不能用于测定粗粒土的静止侧压力系数。这是因为这2种方法的静止侧压力都是通过水囊或橡皮膜来传递,在对粗粒土进行试验时,粗颗粒会引起橡胶囊产生嵌入作用,导致无法修正且不能忽视的误差。此外,现有的经验公式都是针对砂土或黏性土提出的,如利用它们推求粗粒土的K0,其准确性仍需进一步研究。

为得到较为可靠的粗粒土的K0,笔者对长河坝水库大坝地基覆盖层料进行大型单向压缩试验,利用土压力盒同时测定试样内部的水平应力和竖向应力,进而计算得到K0。比较分析了目前常用的计算K0的经验公式对粗粒土的适用性。

1 试验方案及方法

1.1 试验材料

试验所用材料是长河坝土石坝地基覆盖层砂卵砾石风干料。由于原级配最大粒径较大,因此,必须对原级配进行缩尺后才能用于试验,缩尺方法为等量代替法[14]。

经过等量代替法缩尺,得到最大粒径分别为20 mm和60 mm的替代料。2种土料分别编号为D20和D60。试样控制密度分别为2.22 g/cm3和2.30 g/cm3。原级配与试验级配见表1。

表1 砂卵砾石料颗粒级配

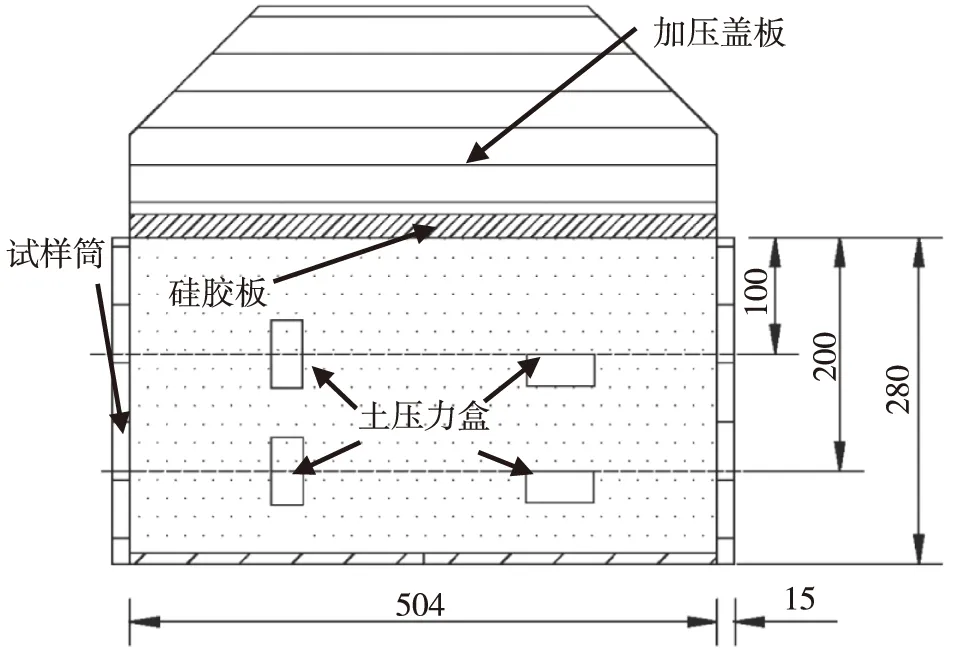
图1 试验仪器示意图(单位:mm)Fig. 1 Sketch of test equipment (units: mm)

1.2 试验仪器

试验所用大型单向压缩仪及土压力盒埋置位置如图1所示。大型压缩仪的直径504 mm,深度280 mm。

为保证土压力的测量精度,在一次试验中,各采用2只钢弦式土压力盒在不同深度处测量试样的水平、竖向应力。4个土压力盒的编号分别为1201、1202、2201、2202。由图1可知,同一高度处,竖向埋设的土压力盒测得水平应力,水平埋设的土压力盒测得竖向应力,这2个应力可认为试样内部同一位置的应力状态,则它们的比值即为试样的静止侧压力系数。

为避免土压力盒侧面或底面与土样接触而引起钢弦频率变化,在土压力盒的外表面套一个稍大的钢杯,钢杯的深度与土压力盒高度相同,内径比土压力盒直径略大,使土压力盒只有受力面与土样接触;同时,用布袋包裹粒径为2～5 mm的砾石制成砾石包放在土压力盒表面,避免土压力盒与粒径较大的土样直接接触,引起土压力盒表面受力不均。

钢弦式土压力盒通过自带的频率计测定钢弦频率的变化,并根据下式计算作用于土压力盒表面的压力:

(7)

式中:K——压力盒灵敏系数,可由土压力盒标定试验曲线确定;f——外力p作用于土压力盒表面时,频率计测得的频率;f0——土压力盒的初始频率,可由标定曲线确定,也可直接由频率计测得,本文将土压力盒埋置在试样内部并覆上砂包时的频率计读数作为初始频率。

目前大多数土压力盒的参数K可直接根据厂家提供的土压力盒在水压作用下的标定曲线确定,这种标定方法称为水压标定法(简称水标法)。笔者采用编号为1201、1202、2201、2202的4个土压力盒根据水标法得到的参数K分别为0.449、0.595、0.962、0.977。

由于土压力盒在土中的受力环境与在水中的受力环境相差较大,将水标法测定的参数直接用来计算土压力盒在土中受到的压力可能会产生误差。陈春红等[15]也曾有类似怀疑,为此,他们对土压力盒进行砂压标定试验,并就土压力盒的标定问题进行了初步探讨。为进一步检验水压标定法的可靠性,笔者对本文试验中用到的土压力盒也采用砂压标定法(简称砂标法)进行了标定。

砂标法试验具体步骤为:将高度30 mm、直径58 mm的土压力盒水平放在深度为120 mm、边长为180 mm的标定罐底部中心处；然后填入覆盖层中的细料作为标定介质,标定介质上放置弹性较好的厚度约20 mm的硅胶板以均匀传力；再加180 mm×180 mm的钢板盖;最后,在钢板盖上分级施加压力,得出土压力盒的标定曲线。从而,确定土压力盒1201、1202、2201、2202标定参数K分别为0.367、0.331、0.453、0.758。

由于土压力盒受力面的感应膜与其周边的压力盒边框刚度不同,因此其变形也不同,会产生所谓的“拱效应”。根据澳大利亚Trollope等[16]的理论:当土压力盒受力面上土层厚度大于土压力盒有效直径的0.9倍以上时,可以不考虑拱效应。上述标定试验中,土压力盒受力面上的土层厚度约90 mm,大于土压力盒直径的0.9倍,因此,拱效应可以忽略。

1.3 测定K0的试验方法

利用大型单向压缩仪测定静止侧压力系数的试验方法是:在压缩仪中分层制备试样,每层试样需击实至预定高度后方可添加下一层土料,每层预定的击实高度根据预定的密度确定。在试样制备过程中,将2个土压力盒1201与1202竖向埋置,其受力面中心到试样顶面距离分别为100 mm和200 mm,用于测定试样不同深度处水平应力;同样,为测定试样不同深度处竖向应力,将2个土压力盒2201和2202水平埋置,其受力面中心与试样顶面的距离分别为100 mm和200 mm。

试样制备完成后,在其表面分级施加压力0～1 000 kPa,通过频率计读取各级压力下土压力盒的频率,利用式(7)计算土样的水平应力和竖向应力。每种土料都进行了3组平行试验。

上述试样中,土压力盒上覆土层厚度至少100 mm,大于土压力盒直径58 mm,故本试验可以不考虑拱效应。

2 标定方法适用性分析

影响土压力盒量测精度的因素较多,如果土压力事先已知,而用土压力盒测得土样的应力与该已知土压力一致,则说明所采用的标定参数适用于该土样,即此标定方法对于该土样来说是可靠的。基于这样的想法,笔者首先利用D60试样进行了标定方法验证试验,以对本文采用的2种标定方法相对于粗粒土的适用性及可靠性进行分析。该试验仍然利用大型压缩仪,在距试样表面某深度处水平埋设(相互之间有一定距离的)4只土压力盒,测定该深度处的竖向应力。试验进行了2次,第一次试验的土压力盒埋置深度100 mm,第二次为200 mm。

在单向压缩试验中,施加在试样表面的压力是明确的。但是,由于试样筒侧壁摩擦力的影响,试样内部竖向应力随深度会逐渐减小。假定对应土压力盒受力面处的竖向应力等于试样表面压力减去侧壁摩擦力引起的竖向应力减小值,并假定试验时土样与试样筒之间的摩擦力达到最大的静止摩擦力,则可推导得到距离试样顶面深度H处的竖向应力为

(8)

式中:σ——土压力盒受力面中心处试样竖向应力;σ1——试样顶部竖向应力,即试验施加的表面压力;K0——试样D60的静止侧压力系数,取本文试验最终结果0.39;H——加载前土压力盒受力面中心处距试样顶面的距离;R——试样筒半径252 mm;α——试样与试样筒侧壁接触面摩擦角,根据文献[17](文献所用土料和侧壁材料与本文一致),取21°。

由式(8)可整理得到H深度处各级表面压力下土压力盒受力面中心处的竖向应力,以下称竖向应力计算值,由于式(8)中各参数都是严格按照本文试验条件测得,其误差不大,可近似作为真实值来检测试验结果。另外,对应各级压力下由水平向放置的土压力盒的频率计读数及其标定参数可计算得土压力,以下称竖向应力量测值。这里,土压力盒采用了2种标定方法,即水标法和砂标法,其标定参数K不同,对应相同表面压力下的竖向应力量测值也是不同的。为检验哪种标定方法能得到更准确的结果,图2(a)和图2(b)分别给出了不同深度处的竖向应力计算值，以及基于2种标定方法得到的竖向应力量测值与表面压力的关系曲线。其中,某深度处竖向应力量测值是水平向埋置在该深度处4个土压力盒所得数据的平均值。

图2 竖向应力计算值及量测值与表面压力关系曲线Fig. 2 Relationship between calculated and measured vertical stresses and surface pressure

由图2可知,在相同深度处同一表面压力作用下砂标法得到的竖向应力量测值及计算值大体相同,说明砂标法得到试样内应力较接近实际值(即真值),对于粗粒土来说是一种相对合理的测试方法。而基于水标法测得的竖向应力量测值与实际值相差较大,显然采用水标法标定的参数计算粗粒土的应力时会产生较大误差,因此不宜用来测定粗粒土土压力。

实际上,由于侧壁摩擦力的存在,而且摩擦力很可能未必全部发挥,因此,式(8)在这里的应用也是近似的。要准确获得试样内的真值应力,需彻底解决摩擦力问题,目前还难以做到。

3 粗粒土K0试验结果可靠性分析

综上可知，砂标法是一种适用于粗粒土的标定方法,为探讨粗粒土K0试验结果的可靠性,做2种土料的静止侧压力系数K0与竖向应力关系曲线,如图3所示。图中,竖向应力是基于砂标法的标定参数得到的竖向应力量测值,K0为同一竖向应力量测值下不同深度处K0的平均值。

图3 K0与竖向应力关系曲线Fig. 3 Relationship between K0and vertical stress

从图3可以看出,静止侧压力系数K0随着竖向应力的增大逐渐减小,且这一现象对试样D60更为明显。这是因为在制样时,土压力盒预先埋入试样,并同试样一起经受人工击实。因此,在试样表面加荷之前,土压力盒受力面存在初始应力作用,其钢弦频率增加,类似于黏土的超固结性质。实际上,笔者发现在试验加载前不仅土压力盒的竖向初始应力远大于它上部土体自重引起的应力,并且此时的竖向应力通常小于水平向应力。因此,施加表面压力之前的K0会偏大。但随着竖向应力增大,击实制样产生的初始应力的影响逐渐减小,从而K0会随竖向压力增大而减小。同时,试样干密度越大,表示压实越紧密,超固结越强,初始水平应力与竖向应力比值也越大。因D60试样密度比D20试样密度大,故D60试样的K0在试验荷载200 kPa时较D20大,但其值随竖向应力的增加而减小得更显著。因此当竖向应力较大时,测得的静止侧压力系数并不会由于击实制样(类似超固结现象)造成较大影响。

综上,对击实密实试样,K0试验在竖向应力较小时由于类似超固结现象影响,K0测得值偏大,而当竖向应力较大时由于类似超固结现象的消除,所得到的静止侧压力系数较为准确。因此,这里取竖向应力较大时测得的试验结果平均值作为试样静止侧压力系数值,则2种级配料D20与D60的静止侧压力系数近似为0.41和0.39。

另外,文献[18]基于现场载荷试验的变形计算公式,推导了正常固结土的静止侧压力系数计算公式:

(9)

式中:ω——沉降系数,取ω=0.88;P、S——P-S曲线上的各级荷载值和沉降量;B——承压板的直径;Es——地基土的侧限压缩模量。

文献[19]通过现场载荷试验获得长河坝覆盖层的P-S曲线,从而获得土料参数P和S。通过室内压缩试验,分别获取D20土料与D60土料的侧限压缩模量。结合式(9),求得D20土料与D60土料的静止侧压力系数约为0.42～0.46,与试验测得的结果相差不大,也说明了本文试验结果的可靠性。

4 粗粒土K0的估算方法

静止侧压力系数K0可以通过试验测定,但是,由于该试验为非常规试验,相关研究相对较少，因此,不少学者总结出一些经验公式来计算K0[4-9]。由于粗粒土颗粒粒径较大,适合它的试验很少,更需要寻找合适的经验公式计算粗粒土的静止侧压力系数。为此,笔者将普通中三轴CD试验测得的内摩擦角代入几种常用的经验公式中计算得出静止侧压力系数,并与本文K0试验结果进行比较,来分析现有的经验公式对粗粒土的适用性,从而找出一种适用于粗粒土K0的估算方法。

笔者对D20土料与D60土料进行普通中三轴CD试验,通过线性摩尔-库伦强度理论整理三轴试验结果,得到土料D20与D60的内摩擦角分别为40.1°、43.6°。

表2 不同方法计算得到的K0

将普通中三轴CD试验测得的D20与D60土料内摩擦角代入式(1)直接计算K0,同时,将它们代入式(3)～(6)分别计算得到已激发角,再将各自得到的已激发角分别代入式(2)计算出2种土料的K0。各种估算方法计算得到的K0列于表2,同时,将本文试验所测得的K0也一并列入表2进行对比。

由表2可以看出,采用Jaky[4]提出的经典经验公式求得的K0明显偏小,不适用于粗粒土。采用Terzaghi[5]提出的式(2)结合Federico等[9]提出的式(6)所算出的K0与试验结果最为接近,相差不过0.03,可以用于估算粗粒土静止侧压力系数。

因此,将式(6)与式(2)相结合即得较为适用于粗粒土的估算公式。

(10)

5 结 论

a. 土压力盒砂标法是用于测定粗粒土土压力的一种相对较合理的测试方法。

b. 由于粗粒土试样制备时,在土压力盒上产生类似于黏性土的超固结现象,因而在土压力盒上产生初始应力,在竖向应力较小时,K0较大;但竖向应力较大时,超固结对K0的影响可以忽略。本文K0试验方法对粗粒土来说是一种较可行的测静止侧压力系数的方法。

c. 基于 Terzaghi 提出的已激发角,Federico等[9]提出的估算公式均适用于粗粒土。但是,由于本文只进行了2种土料的试验,因此K0的估算方法还有待更多试验资料的验证。

d. 粗粒土的静止侧压力系数研究较少,经验数据不多。本文只针对砂卵砾石料进行了研究,至于碎石料的K0,还有待进一步研究。

[1] 史江伟,朱俊高,王平,等. 一个粗粒土的非线性弹性模型[J]. 河海大学学报(自然科学版),2011,39(2): 154-160.(SHI Jiangwei,ZHU Jungao,WANG Ping,et al. Nonlinear elastic model for coarse-grained soils[J]. Journal of Hohai University(Natural Sciences),2011,39(2): 154-160.(in Chinese))

[2] GARGA V K, KHAN M A. Laboratory evaluation ofK0for overconsolidated clays[J]. Canadian Geotechnical Journal, 1991, 28(5): 650-659.

[3] CHEN T J, FANG Y S. A new facility for measurement of earth pressure at-rest[J]. Geotechnical Engineering,2002, 33(3): 113-131.

[4] JAKY J. The coefficient of earth pressure at rest[J]. Journal of the Society of Hungarian Architects and Engineers, 1944, 78(22): 355-358.

[5] TERZAGHI C. Discussion of lateral earth pressure: the accurate experimental determination of the lateral earth pressure, together with a resume of previous experiments[J]. Transactions of the American Society of Civil Engineers,1923,86:1525-1543.

[6] ABDELHAMID M S, KRIZEK R J. At-rest lateral earth pressure of consolidating clay[J].Journal of the Geotechnical Engineering Division, 1976, 102(7): 721-738.

[7] HAYAT T M. The coefficient of earth pressure at rest[D]. Champaign-Urbana:University of Illinois at Urban Illinois a-Champaign, 1992.

[8] SIMPSON B. Retaining structures: displacement and design[J]. Géotechnique, 1992, 42(4): 541-576.

[9] FEDERICO A, ELIA G, GERMANO V. A short note on the earth pressure and mobilized angle of internal friction in one-dimensional com-pression of soils[J]. Journal of Geoengineering, 2008, 3(1): 41-46.

[10] 王俊杰,郝建云. 土体静止侧压力系数定义及其确定方法综述[J]. 水电能源科学,2013(7):111-114.(WANG Junjie, HAO Jianyun. The summary of determination and the definition of lateral pressure coefficient at rest[J]. Water Resources and Power,2013(7):111-114. (in Chinese))

[11] 强跃,赵明阶,林军志,等. 静止土压力系数探究[J]. 岩土力学,2013,34(3):727-730.(QIANG Yue,ZHAO Mingjie,LIN Junzhi,et al. Research on coefficient of earth pressure at rest[J]. Rock and Soil Mechanics,2013,34(3):727-730 (in Chinese))

[12] 宋飞, 张建民, 刘超. 各向异性砂土K0试验研究[J]. 岩土力学, 2010, 31(12): 3727-3732.(SONG Fei, ZHANG Jianmin, LIU Chao. Experimental study ofK0of anisotropic sand[J]. Rock and Soil Mechanics, 2010, 31(12): 3727-3732. (in Chinese))

[13] 贾宁. 有限填土静止土压力系数计算方法研究[J]. 岩土工程学报, 2012, 34(7): 1333-1337. (JIA Ning. Coefficient of at-rest earth pressure from limited backfill[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1333-1337. (in Chinese))

[14] 朱俊高, 翁厚洋, 吴晓铭, 等. 粗粒料级配缩尺后压实密度试验研究[J]. 岩土力学, 2010, 31(8): 2394-2398.(ZHU Jungao, WENG Houyang, WU Xiao-ming, et al.Experimental study of compact density of scaled coarse-grained soil[J]. Rock and Soil Mechanics, 2010,31(8): 2394-2398. (in Chinese))

[15] 陈春红,刘素锦,王钊. 土压力盒的标定[J]. 中国农村水利水电,2007(2): 29-32.(CHEN Chunhong, LIU Sujin, WANG Zhao. Calibration of earth pressure cell[J]. China Rural Water and Hydropower, 2007(2): 29-32. (in Chinese))

[16] TROLLOPE D H, ZAFAR S M. A study of the shear strength of saturated sand, and sand: clay mixtures, in triaxial compression[J]. New Zealand Engineering, 1955, 10(11): 417-425.

[17] 吴中凡. 钢-土接触面试验及直剪试验数值分析[D].南京:河海大学,2014.

[18] 王运霞,李涛. 依据现场载荷试验结果计算静止侧压力系数的探索[J]. 北京交通大学学报(自然科学版),2006,30(4):39-45.(WANG Yunxia, LI Tao. Study on Calculation of coefficient of lateral pressure at rest according to loading test in site[J].Journal of Beijing Jiaotong University (Natural Science), 2006, 30(4): 39-45. (in Chinese))

[19] 沈靠山. 覆盖层砂卵砾石料静止侧压力系数研究[D].南京:河海大学,2009.

Experimental study of at-rest lateral pressure coefficient of coarse-grained soil

ZHU Jungao1, 2, JIANG Mingjie1, 2, SHEN Kaoshan3, CHU Fuyong4

(1.KeyLaboratoryofMinistryofEducationforGeomechanicsandEmbankmentEngineering,HohaiUniversity,Nanjing210098,China;2.GeotechnicalResearchInstitute,HohaiUniversity,Nanjing210098,China;3.ZhejiangQianTangRiverManagementBureauSurveyDesignInstitute,Hanzhou210098,China;4.SchoolofCivilEngineering,LishuiUniversity,Lishui323000,China)

A large-scale uniaxial compression test was conducted for two types of graded sand-grained materials from the overburden of a dam. The horizontal stress and vertical stress of sand-grained materials were measured using soil pressure boxes with parameters obtained from a calibration method, and then the at-rest lateral pressure coefficient (K0) was calculated. By studying the applicability of the hydraulic and sand calibration methods, the reliability of the experimental results ofK0was analyzed. The results show that the sand calibration method is a reliable calibration method for coarse-grained soil. When the vertical stress is large enough, the experimental error ofK0can be ignored, and the value ofK0is close to the actual value. The triaxial CD test was conducted for two types of graded sand-grained materials to measure the effective angle of internal friction, and thenK0was calculated through the relevant empirical formula and compared with the test value to obtain an empirical formula that is suitable for coarse-grained soil. The results show that the relationship expression between the at-rest lateral pressure coefficient and the effective angle of internal friction, which was proposed by Federico and was based on the concept of a mobilized effective angle of internal friction proposed by Terzaghi, is appropriate for coarse-grained soil.

coarse-grained soil; at-rest lateral pressure coefficient; large-scale uniaxial compression test; soil pressure box; effective angle of internal friction; mobilized effective angle of internal friction

10.3876/j.issn.1000-1980.2016.06.004

2015-12-02

国家自然科学基金(51479052); 浙江省自然科学基金(LY14E080004);江苏省普通高校研究生科研创新计划(20141B1605313)

朱俊高(1964—)，男，江苏兴化人，教授，博士，主要从事土石坝研究。E-mail：jake307562306@vip.qq.com

TU411

A

1000-1980(2016)06-0491-07