北太平洋海浪特征分析

诸裕良,徐秀枝

(1. 江苏省海岸海洋资源开发与环境安全重点实验室,江苏 南京 210098;2. 河海大学港口海岸与近海工程学院,江苏 南京 210098)



北太平洋海浪特征分析

诸裕良1,2,徐秀枝2

(1. 江苏省海岸海洋资源开发与环境安全重点实验室,江苏 南京 210098;2. 河海大学港口海岸与近海工程学院,江苏 南京 210098)

利用最新的欧洲中尺度天气预报中心(ECMWF)提供的1979—2014年逐6 h的ERA-Interim有效波高和风速数据,分析近36 a北太平洋海浪场的变化特征。结果表明:有效波高经验正交函数分解(EOF)的第1模态呈同相位分布,该模态与太平洋10 a涛动指数(PDO)和厄尔尼诺事件(ENSO)呈显著的遥相关,可以通过这些气候因子的变化来预测有效波高的年代际变化;第2模态表明北太平洋西部海域的有效波高有显著的递增趋势,而东部海域则逐渐减小;第3模态以45°N为界,西风带呈现高低纬反相的双涡型分布,并有显著的2.5 a左右年际变化周期。北太平洋海域有效波高和风速重现期极值的大值区位于西风带,重现期越长,日本群岛南部海域风速加强越显著,加强的极值区延伸到中国的东海甚至是菲律宾群岛的东部海岸。

ERA-Interim;北太平洋;海浪特征;有效波高;EOF分解;重现期极值

在海洋工程中,海浪是最活跃、最重要的动力要素。海洋自然灾害不仅对沿海建筑物及海上航行条件构成威胁,还严重影响人民生命财产的安全。目前兴起的海上风力发电和海洋石油平台建设等的设计都需要用到波高的重现期极值,以确保建筑物的持久使用,所以了解海浪的变化特征对工程建筑物的建设和沿海社会经济的发展有重要意义。

国内外有诸多学者对海浪以及极值事件进行了研究。Carter等[1]、Bacon等[2]整理北大西洋的观测数据资料,分析发现北大西洋海域可能从20世纪50年代起有效波高就开始以一定的速度在增加;张弦等[3]利用1950—1995年共46 a的南印度洋船舶气象报资料,分析研究了南印度洋的海浪要素。但是他们使用的观测数据长度以及空间分辨率有限,很难确保实测资料时空序列的均一性。在20世纪70年代随着观测卫星相继发射成功,大量的海洋观测数据诞生。卫星高度计资料在海洋波浪研究中的应用日渐增多,加上数据同化技术以及数值模式的发展,海洋的研究进入一个新的阶段[4-5]。Swail等[6]基于用美国国家环境预报中心(NCEP)提供的风场数据，利用数值模拟的方法进行了一系列的数值实验,研究了北大西洋的波候变化情况,并对其进行修正,将实验结果与浮标观测数据进行对比,得到了可靠的数值模拟结果。Kushnir等[7]利用数值模式和相关性分析手段,对北大西洋地区的海浪场和海平面压力做了相关分析,结果表明该地区波候的变化与北大西洋涛动(NAO)存在线性相关关系。Caires等[8]利用欧洲中尺度天气预报中心(ECMWF)提供的ERA-40再分析数据集,计算了全球百年一遇的风速、波高极值,并利用浮标实测数据进行修正,得到重现期要素的变化情况。Yang等[9]利用1989—2008年ECMWF的数据和再分析数据等的风场数据，研究了渤海湾风速和有效波高的联合概率分布，得到渤海湾海域的波浪主要为风浪。郑崇伟等[10]同样利用欧洲中尺度天气预报中心(ECMWF)提供的45 a的ERA-40海浪资料,对太平洋的海表风场、浪场特征进行分析,发现太平洋大部分海域的涌浪波高、混合浪波高呈显著的逐年线性递增趋势。

我国濒临西北太平洋,深入了解太平洋海域的海洋环境特征,对海洋开发、海洋工程、防灾减灾、远海国防等都具有极为重要的意义。而目前对太平洋海域的波候变化特征还没有系统的研究,此外,数据集精度也限制其发展。近几年,ECMWF发布了一个最新的再分析同化数据集ERA-Interim[11],它比ERA-15和ERA-40数据集更加精确,耦合了大气、海洋和陆地模型,采用最新的四维变分分析同化技术,结合改进的湿度分析、卫星数据误差校正等技术,实现了再分析资料质量的提升。本文采用ERA-Interim数据集对北太平洋海域的海浪场特征进行分析。

1 数据来源及方法介绍

文章采用ECMWF中ERA-Interim数据集提供的有效波高(Hs)和10 m风场数据,其时间分辨率为6 h,空间分辨率为0.75°×0.75°,时间跨度为1979年1月至2014年12月,计算范围为0°～70°N,100°E～100°W。在进行统计分析的时候主要用到的分析方法是经验正交函数分解(EOF)方法和极值估计方法。EOF方法是一种分析波候变化特征的主要方法[12-13],它可以将随时间变化的变量场分解为不随时间变化的空间函数部分以及只依赖时间变化的时间函数部分[14]。采用一元线性回归来分析时间序列的变化趋势,再采用相关性分析进行显著性检验,其表达式为

(1)

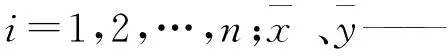
γ的范围为-1～1,γ的绝对值越大,表示2个变量的相关程度越高。通常给出显著性水平为α时相关系数达到显著的最小值γα,若|γ|>γα就说明相关系数显著,否则说明相关系数不显著。

极值估计方法目前常用的主要有皮尔逊Ⅲ型曲线法、耿贝尔(Gumbel)曲线法和威布尔(Weibull)曲线法。皮尔逊Ⅲ型曲线是皮尔逊曲线族中的一种线型,为纯经验型,在海洋学的极值统计中很常用。耿贝尔分布即为Fisher-TippettⅠ型极值分布,主要应用于降水、气温、风速及波高等水文气象要素的推算中。耿贝尔曲线最大项的极值分布函数为

(2)

式中:a——极值分布的众值；b——常数。求解这2个参数的方法有矩法、最小二乘法、极大似然法等,本文采用最小二乘法求解。

威布尔分布近些年来被广泛用于风速和波高最大值重现期的计算。它的分布函数为

(3)

式中:c——位置参数;β——尺度参数；η——形状参数。常用的求解参数方法有最小二乘法、概率权重矩法和极大似然法等,本文采用概率权重矩法[15]求解威布尔3个参数。

2 北太平洋海浪场时空特征分析

表1 1979—2014年北太平洋月平均有效波

2.1 有效波高的EOF分析

将北太平洋海域1979年1月至2014年12月36 a的月平均有效波高距平值做EOF分解,探究其变化特性,为海浪场的经验预测和分析提供一定的参考。表1中列出了前10个模态的方差贡献率。从表1可以看出前10个模态方差贡献率达到81.35%,说明这10个模态基本上可以反映北太平洋月平均有效波高的时空变率特征。

本文主要分析前3个模态的变化规律。为了分析时间序列的变化周期,过滤掉一些高频的信号,对时间序列做11点滑动平均过滤掉年以内的信号,然后对各模态的时间序列进行功率谱分析,得到各个对应的时间序列的振荡周期,分析其年际变化规律。

图1给出了第1模态的空间典型场和对应的时间序列以及功率谱分析图。从图1可以看出整个北太平洋海域第1典型场均为负值,呈现出同相位的变化规律。在西风带内(155°W,40°N)附近出现一个大值中心,且北太平洋东部有效波高的变化明显强于西部海域,西风带强于信风带。这一空间典型场反映了有效波高距平值的平均特征,体现了北太平洋有效波高的空间分布。

为了分析有效波高多种时间尺度上的周期变化,对第1模态时间系数进行11点滑动平均然后再进行谱分析,见图1。功率谱的最大谱峰值(0.083)所对应的周期是5.9 a,表现出显著的年际变化特征。在1982年、1983年和1997年、1998年是历史上的强厄尔尼诺事件(El Nio),1988年、1989年、2000年等是强拉尼娜事件(La Nia),从第1模态图中可以看出这些年份北太平洋的距平有效波高值都发生了异常的减小或者增大,这就说明了这种变化与ENSO事件有可能存在一定的联系。此外,Zhu等[16]指出在20世纪90年代末,太平洋10 a涛动(PDO)指数由正相位转换为负相位,这一变化对全球的气候都产生了一定的影响,而时间序列在1997年前后也发生由负相位到正相位的转换,因此有效波高与PDO也有可能存在一定的内在联系。

图1 有效波高第1模态时空分析Fig. 1 Temporal and spatial analysis of first EOF mode of Hs

图2为第2模态的空间典型场和对应的时间序列以及功率谱分析图。第2模态典型场呈现出东西反相的跷跷板式的变化规律,正负值中心分别在(160°E,35°N)和(135°W,40°N)附近。而且北太平洋西部有效波高的变化比东部海域显著。这一模态典型场对应的时间序列中线性变化趋势的相关系数γ=0.283大于γα=0.097,通过了95%的显著性检验,说明线性增长趋势显著。结合空间典型场的分布特征,说明北太平洋西部海域的有效波高有显著的增加趋势,而东部海区则有逐渐减小的特点。此外,时间序列图中1997年前后,时间系数发生了相位转换,由1997年以前的负异常转换为1997年以后的正异常,时间系数在整体增加的线性趋势上叠加有年际周期振荡,功率谱的谱峰值(0.019)所对应的主周期是2.5 a,表明北太平洋有效波高这种东西反相的分布具有年际变化的特征。

图2 有效波高第2模态时空分析Fig. 2 Temporal and spatial analysis of second EOF mode of Hs

图3为第3模态有效波高的时空分布特征,它的典型场主要表现为北太平洋西风带高低纬反相的双涡型分布特征,以45°N为界,西风带高纬度区域为正相位,低纬度区域为负相位。正负极值中心分别位于(170°W,50°N)和(170°W,35°N)附近。这一空间典型场反映了西风带有效波高距平值的空间分布。时间序列中,线性变化趋势的相关系数γ=0.123大于γα=0.097,通过了95%的显著性检验,说明西风带有效波高线性增长趋势显著。空间典型场和时间序列表明西风带北部(45°N～60°N)呈增加趋势,西风带南部(30°N～45°N)呈减小趋势。同样,在1997年时间系数由负异常转换为正异常。第3模态时间序列的功率谱分析显示,西风带具有2.4 a左右的变化主周期,说明西风带的这种南北反相变化有显著的年际变化。

2.2 有效波高与PDO、ENSO的关系

上文分析得到北太平洋有效波高存在着显著的年际变化,与PDO指数和ENSO事件可能存在一定的联系。所以下面将分析有效波高与这些气候因子的相关性。Nio3.4区(5°N～5°S,170°W～120°W)能很好地监测和反映厄尔尼诺信号,而且该区微小的温度变化也会对气候产生较大的影响[17],因此本文采用Nio3.4区海表温度距平SSTA指数来定义ENSO事件。为了解决数据的可比性,采用Z-score数据标准化将PC1、PDO和Nio3.4指数标准化后再求解它们的相关系数。

图4是北太平洋月平均有效波高经EOF分解后,第1模态的时间序列PC1与PDO、Nio3.4指数的相关性。计算PC1与PDO的相关系数γp为-0.44,与Nio3.4的相关系数γe为-0.53,均通过了95%的显著性检验,说明北太平洋有效波高与PDO和Nio3.4指数存在遥相关且为负相关,当PDO、Nio3.4指数为正相位时,PC1基本为负相位,而PDO、Nio3.4指数为负相位时,PC1基本为正相位。

图3 有效波高第3模态时空分析Fig. 3 Temporal and spatial analysis of third EOF mode of Hs

此外,从图4中还发现,PC1的某些强正负相位刚好对应强ENSO事件的发生。在PC1为强正相位年时,这些年份大多是La Nia事件年,有效波高表现为正异常,而PC1为强负相位年时,大多是El Nio事件年有效波高则表现为负异常,所以北太平洋有效波高存在很强的ENSO信号。而ENSO信号和太平洋10 a涛动都具有显著的年代际变化周期,所以,气候因子的年代际振荡周期可以为有效波高的年代际变化提供一定的预报依据。

图4 有效波高的时间序列PC1与PDO、Nio3.4指数的相关性Fig. 4 Correlations of PC1 of Hs with PDO index and Nio3.4 index

图5 时间序列PC1与Nio3.4指数空间相关性Fig. 5 Spatial distribution of correlation between PC1 and Nio3.4 index

3 有效波高和风速的极值分布特征

海洋的极值风浪通常会造成灾害性的海况,想要确保建筑物的持久使用以及航行安全,仅了解海浪场的平均态特性是远远不够的,像目前兴起的海上风力发电和海洋石油平台建设等的设计都需要用到多年一遇的波高和风速。海洋要素极值的计算是一个严峻又具有重大实际意义的工作,无论对于近岸工程建筑物的持久使用,还是沿海社会经济的快速发展都有密切的关系。所以为了提高建筑物的防御能力以及确保航行及人类的生命财产安全,本节对有效波高和风速的极值分布进行分析研究。

3.1 重现期分布曲线选取

选取不同的分布函数会对有效波高和风速多年一遇重现期结果产生不同的影响,大量的研究表明适用于海洋资料分析的推算极值的概率分布函数主要有皮尔逊Ⅲ型分布(简称P-Ⅲ型),耿贝尔(Gumbel)分布以及威布尔(Weibull)分布[18]。

P-Ⅲ分布曲线在拟合数据时,人为因素太大,不具有客观性,而且在实际的研究分析中,获取的样本数量有限,这就会导致偏态系数的误差很大,所以一般不采用。耿贝尔分布完全为理论分布,但只含有2个参数,在适应数据的能力上不强。相比于耿贝尔分布,威布尔分布更便于应用。威布尔分布一方面是从理论上推导出的分布函数,另一方面又含有3个未知参数,灵活性大,易于与实际资料结合,精度上更高,因此使用广泛。本文采用威布尔三参数分布曲线估计北太平洋有效波高和风速的多年一遇重现期极值。

3.2 北太平洋海域重现期分布

利用ECMWF数据将北太平洋海域每个网格点上1979—2014年的年极值取出,用威布尔分布曲线进行拟合,从而得到北太平洋多年一遇重现期的空间分布特征。图6和图7分别给出了有效波高和风速的多年一遇重现期分布。从图6中可以看出,随着重现期的增加,分布图上的极值也在增加。图6中5 a一遇的有效波高最大值在12.8 m,20 a和50 a一遇的最大值分别为14.2 m和15.0 m,到了100 a一遇的最大值达到了15.8 m。最大值均出现在西风带内,这主要是由于北太平洋高纬度地区气旋活动频繁容易形成风浪和涌浪,所以波高值很大。对于不同重现期,区域的空间分布基本相同,在30°N以北海域受地形的限制呈环状分布,30°N往南有效波高迅速减小,0 °N～30 °N范围大致呈带状递减分布,到赤道区域极值最小,甚至在2 m以下。

图6 有效波高重现期分布Fig. 6 Hs distribution for different return periods

图7中风速的重现期分布与有效波高的相比最大值区域北移,空间上从高纬到低纬度地区呈递减的带状分布,依然是在赤道区域最小。不同重现期风速最大值增加,从5 a一遇的35.4 m/s到100 a一遇的43.6 m/s。从图7中还可以发现,重现期越长,在北太平洋西北部,即日本群岛南部海域风速加强显著,且加强的极值区域呈向西南延伸的舌状,超过50 a一遇后延伸到中国的东海甚至是菲律宾群岛的东部海岸。

图7 风速重现期分布Fig. 7 Wind speed distribution for different return period

4 结 论

利用ECMWF中的ERA-Interim数据集对北太平洋海域1979—2014年的海浪场变化特征进行了分析研究,主要得到以下结论:

a. 北太平洋有效波高EOF分解的第1模态呈同位相分布,且北太平洋东部有效波高的变化明显强于西部海域,这一模态的时间序列与气候因子PDO、ENSO都呈显著的遥相关关系,可以通过气候因子来预测有效波高的年代际变化。

b. 第2模态表现为东西反相的跷跷板式的变化规律,北太平洋西部海域的有效波高有显著的逐年递增趋势,而东部海域则有逐渐减小的特点。第3模态表现为北太平洋西风带高低纬反相的双涡型分布特征,以45°N为界,西风带高纬度区域有效波高增加,低纬度区域有效波高减小。并且以上的变化特征都有2.5 a左右的年际变化规律。

c. 北太平洋海域有效波高和风速重现期极值的大值区都位于西风带内。重现期的增加,分布图上的极值也增加。有效波高最大值从5 a一遇的12.8 m增加到100 a一遇的15.8 m。风速从5 a一遇的35.4 m/s到100 a一遇的43.6 m/s。而且重现期越长,在日本岛南部海域风速加强越显著,加强的极值区延伸到中国的东海甚至是菲律宾半岛的东部海岸。有效波高和风速的重现期极值计算可为深海操作提供一定的量化指导。

[1] CARTER D J T, DRAPER L. Has the north-east Atlantic become rougher? [J]. Nature, 1988, 332(6164): 494-506.

[2] BACON S, CARTER D J T. Wave climate changes in the North Atlantic and North Sea [J]. International Journal of Climatology, 1991, 11(5): 545-558.

[3] 张弦, 刘金芳, 张学宏, 等. 南印度洋海浪场时空特征分析[J]. 海洋通报, 2003, 22(2): 25-31. (ZHANG Xian, LIU Jinfang, ZHANG Xuehong, et al. Annual variation analysis of sea wave field in the South Indian Ocean [J]. Marine Science Bulletin, 2003, 22(2): 25-31. (in Chinese))

[4] 葛黎丽, 屈衍, 张志旭, 等. 南海深水区风, 浪, 流多年一遇重现期极值的推算[J]. 中国海上油气, 2009, 21(3): 207-210. (GE Lili, QU Yan, ZHANG Zhixu, et al. The calculation of the extreme wind, wave and current for return periods in the deep water area of the South China Sea [J]. China Offshore Oil and Gas, 2009, 21(3): 207-210. (in Chinese))

[5] 庄晓宵, 林一骅. 全球海洋海浪要素季节变化研究[J]. 大气科学, 2014, 38(2): 251-260. (ZHUANG Xiaoxiao, LIN Yihua. Seasonal variation of global ocean wave [J]. Chinese Journal of Atmospheric Sciences, 2014, 38(2): 251-260. (in Chinese))

[6] SWAIL V R, COX A, CARDONE V. Trends and potential biases in NCEP-driven ocean wave hindcasts[C]//.World Climate Research Program.In Proceedings of the Second WCRP International Conference on Reanalyses. Geneva: WCRP , 1999: 23-27.

[7] KUSHNIR Y, CARDONE V J, GREENWOOD J G, et al. The recent increase in north atlantic wave heights[J]. Journal of Climate, 1997, 10(8): 2107-2113.

[8] CAIRES S, STERL A. 100-year return value estimates for ocean wind speed and significant wave height from the ERA-40 data [J]. Journal of Climate, 2005, 18(7): 1032-1048.

[9] YANG X， ZHANG Q. Joint probability of winds and waves from wave simulation of 20 years(1989—2008) in Bohai Bay[J]. Water Science and Engineering, 2013, 6(3): 296-307.

[10] 郑崇伟, 林刚, 孙岩, 等. 近 45 年太平洋海浪特征分析[J]. 热带海洋学报, 2012, 31(6): 6-12. (ZHENG Chongwei, LIN Gang, SUN Yan, et al. Analysis of wave characteristics in the Pacific Ocean during the last 45 years [J]. Journal of Tropical Oceanography, 2012, 31(6): 6-12. (in Chinese))

[11] DEE D P, UPPALA S M, SIMMONS A J, et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system[J]. Quarterly Journal of the Royal Meteorological Society, 2011, 137(656): 553-597.

[12] GULEV S K, GRIGORIEVA V. Variability of the winter wind waves and swell in the North Atlantic and North Pacific as revealed by the voluntary observing ship data [J]. Journal of Climate, 2006, 19(21): 5667-5685.

[13] SEMEDO A, SUELI K, RUTGERSSON A, et al. A global view on the wind sea and swell climate and variability from ERA-40[J]. Journal of Climate, 2011, 24(5): 1461-1479.

[14] 刘婷婷, 张华. 主成分分析与经验正交函数分解的比较[J]. 统计与决策, 2011 (16): 159-162. (LIU Tingting, ZHANG Hua. Principal component analysis was compared with the empirical orthogonal function decomposition [J]. Statistics and Decision, 2011(16): 159-162. (in Chinese))

[15] 张秀芝. 概率权重矩法及其在Weibull分布参数估计中的应用[J]. 海洋预报, 1994, 11(3): 55-61. (ZHANG Xiuzhi. Application of probability weighted moments to estimate parameters in Weibull distribution [J]. Marine Forecasts, 1994, 11(3): 55-61. (in Chinese))

[16] ZHU Y, WANG H, ZHOU W, et al. Recent changes in the summer precipitation pattern in East China and the background circulation [J]. Climate Dynamics, 2011, 36(7/8): 1463-1473.

[17] 许武成, 王文, 马劲松, 等. 1951—2007年的ENSO事件及其特征值[J]. 自然灾害学报, 2009, 18(4): 18-24. (XU Wucheng, WANG Wen, MA Jingsong, et al. ENSO events during 1951-2007 and their characteristic indices [J]. Journal of Natural Disasters, 2009, 18(4): 18-24. (in Chinese))

[18] 陈上及, 马继瑞. 海洋数据处理分析方法及其应用[M]. 北京: 海洋出版社, 1991.

Analysis of wave characteristics in North Pacific Ocean

ZHU Yuliang1,2, XU Xiuzhi2

(1.JiangsuKeyLaboratoryofCoastOceanResourcesDevelopmentandEnvironmentSecurity,Nanjing210098,China；2.CollegeofHarbour,CoastalandOffshoreEngineering,HohaiUniversity,Nanjing210098,China)

Using the latest ERA-Interim sea surface wind field and wave field data from every 6 h from 1979 to 2014 provided by the European Centre for Medium-Range Weather Forecasts (ECMWF), the wave characteristics in the North Pacific Ocean for the last 36 years were analyzed. The results show that the first mode decomposed from the empirical orthogonal function (EOF) of significant wave height (Hs) exhibits in-phase change rules and is teleconnected with the Pacific Decadal Oscillation (PDO) and El Nio-Southern Oscillation (ENSO); the second mode shows thatHsexhibits a significant increasing trend in the western region of the North Pacific Ocean, and a gradually decreasing trend in the eastern region of the North Pacific Ocean; and the third mode mainly exhibits inverse double-eddy-type distributions at high and low latitudes in the westerlies, with 45°N as a boundary. The maximum extremes ofHsand wind speed for different return periods appear in the westerlies; for a relatively long return period, wind speed shows a significant increase in the area to the south of Japanese islands. The area with increased extremes extends to the East China Sea or even the east coast of Philippine islands.

ERA-interim; North Pacific Ocean; wave characteristic; significant wave height; empirical orthogonal function decomposition; extreme for return period

10.3876/j.issn.1000-1980.2016.06.013

2016-03-20

中央高校基本科研业务费专项(2016B10414,2016B20814,2015B26414)

诸裕良(1965—),男,江苏无锡人,教授,博士,主要从事水动力研究。E-mail:zhuyl@hhu.edu.cn

P73

A

1000-1980(2016)06-0550-08