抗体监测抽样数量及结果判定的有关讨论与演算

李　印，张美晶，沈朝建，孙向东，康京丽，黄保续，王幼明（中国动物卫生与流行病学中心，山东青岛　266032）

抗体监测抽样数量及结果判定的有关讨论与演算

李印，张美晶，沈朝建，孙向东，康京丽，黄保续，王幼明
（中国动物卫生与流行病学中心，山东青岛266032）

为详细阐述抗体监测中抽样数量及合格群体判定标准等问题，进而为相关人员提供科学参考，本文对相关流行病学原理进行了介绍，对国内在免疫后抗体监测中抽样数量及结果判定等方面存在的争议进行了系统分析，并通过计算给出了不同规模场户评价免疫合格率时的抽样量及结果判定方法。分析结果证实了目前我国在免疫抗体监测中存在不足，并说明了为何不应固守“70%抗体免疫合格率”这一指标的理由。这些结果为进一步改进动物免疫后的抗体监测提供了借鉴。

兽医流行病学；抗体监测；抽样；群体免疫；传染病动力学；

疫苗免疫是防治动物疫病的重要手段。我国自2001年开始，在每年春秋两季集中对部分重大动物疫病实施强制免疫。目前我国实行强制免疫的动物疫病有高致病性禽流感、口蹄疫、猪瘟、布鲁氏菌病和高致病性蓝耳病等[1]。

为了解免疫效果，通常在免疫一定时间后，采集动物血清进行抗体检测。通过抗体检测，评价个体抗体合格率，并评价群体抗体水平。除此之外，抗体监测还可以评价不同疫苗的免疫效果。因此科学合理的采样及结果分析是实现这些目的的基础。

在具体工作实践中，很多人对抗体监测中抽样数量及合格群体判定标准等问题认识不清。本文介绍了相关流行病学原理，系统剖析了国内在免疫后抗体监测中抽样数量及结果判定等方面存在的争议，并通过计算给出了不同规模场户评价免疫合格率时的抽样量及结果判定方法。

1　免疫后抗体监测抽样量的争议：太多还是太少？

我国目前通常采取每个场户抽取30头/只动物血清，以其中抗体合格个体占比是否超过70%（即21个）作为该群体是否为免疫合格场户的判定标准。其中有两个问题经常引起争议：一是30个样本是否合适？二是为什么群体免疫合格的阈值定为70%？关于这两个问题，需要首先了解抽样量计算及群体免疫的原理。

1.1发现疫病或证明无疫的抽样量计算

现实工作中，往往需要通过抽样检测来确定一个场群内是否有无某种疫病。通过抽样来发现疫病，需要设定两个指标：一是置信水平，即对结果的把握度，一般设定为95%；二是该病可能的最低流行率，即该病在群体中可能的最小流行率。此时所需最小抽样量计算公式为：

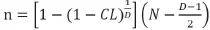
其中：n为抽样个数；CL为置信水平；N为群内个体数；D为群中的阳性动物数，即D=N×p，p为预设的最低流行率[2]。如果一个鸡场内存在新城疫变异株流行的话，它最低的可能流行率也不会低于10%，此时，依据该公式计算样本量为：

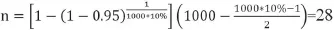
为了简便，此处默认为群体大小为1 000只，规模较小时，需要对样本量进行调整；如无特殊说明，本文默认检测方法的敏感性及特异性均为100%（下同）。

这里的含义是指如果该群体中存在某种疾病，那么抽取28只检测，有95%的把握至少检测到1只感染动物。需要注意的是，这是以发现疫病或证明无疫为目的的抽样量，并且是基于该疫病最低流行率为10%的假设之上。这些假设并非对所有的疫病都合适。现实工作中，往往需要同时采集病原样本和血清样本。其中病原学采样的目的往往是发现疫病，但采集血清的目的却往往是评估抗体合格率是否达到70%。30只的抽样量对于病原学采样可能是合适的（如果一个疫病群内流行率通常高于10%），但是对于评价抗体合格率，则可能存在估计精度不足。但在现实工作中，为了操作便利，采样人员往往选取30头/只动物，同时采集病原学样品和血清学样品。这就是抗体监测时通常采样量为30头/只的原因。

1.2评估流行率的抽样量计算

有时候需要通过抽样估计某种疫病在一个群体中的流行率或者群内的抗体合格率，这时要首先确定几个指标：一是预计该病在群内的可能流行率，即该病在群体内最可能的流行率；二是置信水平，一般设为95%；三是需要估计的精度，即可接受的误差大小。此时的抽样量计算公式为：

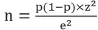
其中：p为预期流行率；z为来自正态分布1-α/2百分位点对应的统计量。对于每一个置信水平，都有一个相应的z值。生物学研究中，常用的置信水平为90%、95%、99%，其对应的z值分别是1.64、1.96、2.58。e为可接受的最大绝对误差[2]。根据上述公式，推导出根据抽样结果推断总体流行率的置信区间为：

1.3每场抽样30只时群体免疫合格的判定

现实工作中，各级动物疫病预防控制机构通常从一个场户中抽取30只动物检测抗体，以21个动物的抗体达标作为群体是否免疫合格的标准。这一标准是否合理呢？根据评估流行率的计算公式，如果从一个大型场户中（如1 000头/只动物）采集30头/只动物血清，其中有21个抗体合格，此时该群内抗体合格率为：21/30=70%，其95%的置信区间为：

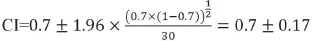
该结果说明，95%的置信度情况下，这个场户内抗体合格率介于53%～87%之间，所以该场户的抗体合格率仍有可能低于70%。再假设另一种情形：某1000头猪场内个体抗体合格率只有60%，如果随机抽取30头检测抗体，抽到合格动物的数量会是多少？如果个体抗体合格率只有65%呢？利用Poptool软件[3]，使用二项分布模拟运算1 000次，得到以上两种情况下该场户抽到抗体合格动物数量的概率分布（图1）。模拟运算结果表明，当场内个体抗体合格率只有60%时，随机抽取30头检测抗体，有17.3%的概率抽到21个以上的阳性动物；当场内个体抗体合格率只有65%时，随机抽取30头检测抗体，则有38.9%的概率抽到21个以上的阳性动物，这种情况发生的可能性已经较高。因此，每场采集30份血清时，以阳性数量高于21个作为判定免疫合格的标准是不够严谨的。

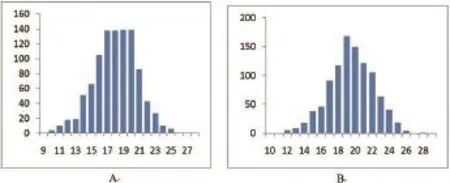
图1　场内个体合格率分别为60%和65%时30份抽样中阳性个体数的概率分布

1.4群体免疫理论及传染病动力学

通常认为群内抗体合格率达到70%以上时，该群体就是一个免疫合格群，就会因抗体保护而对某些疫病具有免疫力。这一说法来源于“群体免疫”这一概念[4-5]。简单地说，该理论认为如果一个群体内具有免疫力的个体达到一定比例，那么即使有病原进入到该群体内，也不能引发疫病流行，该群体就具有了“免疫力”，不会被感染。

70%这一数字来源于传染病动力学有关数学模型模拟计算的结果。1926年Kermack和McKendrick为了研究1665—1666年黑死病在伦敦的流行规律，以及1906年瘟疫在孟买的流行规律，构造了著名的SIR仓室模型[6]。该模型的基本思想一直到现在仍然被广泛使用和不断发展，并衍化出许多其它模型。所谓SIR仓室模型就是针对某种传染病，将一个群体内的个体分为三类（即三个仓室）：

易感者（Susceptibles）：其数量记为S（t），表示t时刻未染病但有可能被该类疾病传染的个体数；

感染者（Infectives）：其数量记为I（t），表示t时刻已经染病而且有传染力的个体数；

移出者（Removed）：其数量记为R（t），表示t时刻已经从感染者中移出的个体数。

传染病流行期间，群体内个体不断在三个仓室中转换。假设群体总个体数为N（t），则有N（t）= S（t）+ I（t）+ R（t）。

该模型的建立基于以下三个基本假设：

一是群体在研究时段内为封闭群体。群体中的总个体数保持稳定。群体规模较大时，可视为其个体数在一段时间内稳定；

二是一个感染者与易感者接触就必然具有一定传染力。假设t时刻单位时间内，1个感染者能够传染的易感者数量与此环境内易感者总数S（t）成正比，比例系数为β，则t时刻单位时间内被所有感染者传染的新病例数为βS（t）I（t）；

三是t时刻单位时间内从感染者中移出的个体数与感染者数量成正比，比例系数为γ，从而单位时间内移出者数量为γI（t）。

该模型经过演算，得出一个重要参数：基本再生数（R0）。其含义为1个感染者在其整个传染期内通过与易感者有效接触可以传染的新病例期望数。如果R0>1，则1个感染者将会传染给1个以上的易感者，那么新病例将越来越多，疾病就会流行；如果R0<1，则1个感染者将会传染给少于1个的易感者，那么新病例将越来越少，疾病流行就会逐渐停止。如果需要在一个地区消灭某传染病，需要采用多种措施使得R0<1。

由公式：R0=βS0/γ可知，需要使三个参数尽量减小，它们各自的含义及相关影响因素见表1。

根据表1可知，疫病是否会流行不仅与免疫覆盖率有关，而是由多种因素共同决定的。不同的疫病种类、不同的易感动物群体、不同的养殖和交易模式，应该会得到不同的免疫合格阈值。甚至在不同地区对同一种疫病开展强制免疫时，因为养殖密度、动物品种、养殖和交易模式不同，需要达到的场户免疫合格率也不同。公共卫生流行病学研究方面有类似例子：如相关研究认为在欧洲消灭麻疹和风疹需要在人群中的免疫密度分别达到96%～99%以上和87%～99%以上[7]；麻疹在美国城镇地区的R0为8.3到13.0，免疫密度要达到88%～92.3%以上才能消灭，而在英国麻疹的R0为12.5到16.3，免疫密度要达到92.9%～94%以上才能消灭[6]。

综上，70%的免疫合格率不可能适用于所有疫病和所有地区，应该根据不同疫病在不同地区的特定流行病学特征，确定不同的免疫合格率要求。

表1　传染病基本再生数相关影响因素

2　抗体监测抽样数量及判定标准

日常工作中，对某一个场户的动物免疫过后，往往需要抽样检测，评价个体抗体合格率是否达到一定比例，比如70%。此时，应该抽多少动物检测，并且对于检测结果如何解读呢？解答这一问题涉及概率分布中的二项分布、负二项分布和超几何分布等数学理论，相关概率分布过于复杂，在此不做交代。利用Freecalc软件中“证明无疫抽样模块”（Free from disease）[8]，计算不同情境下所需要的抽样量，并解读各种情况下的结果判定。为了简化，下面的计算有如下假设：一是群内抽样是以完全随机方式抽取；二是抽样的置信水平和效度均设为95%；三是当抽样检测为完美试验时，总的敏感性和特异性均设为100%，当不完美抽样检测总的敏感性设为90%，特异性设为90%，但实际情况中不同疫病的抽样检测方法总的特异性和敏感性各不相同。

2.1针对小群体抗体监测的抽样

当在小群体中抽样时，经常遇到抽样比例超过10%的情况，此时抽样概率分布应使用超几何分布进行计算。注意，在部分情况下抽样比例虽然并没有超过10%，但因接近10%，此时无论按照超几何分布计算，还是按照二项分布计算，结果都相近。为了简化，将这些情形按照同一种分布计算，一并放在同一张表内。

2.1.1当抽样检测为完美试验时的抽样量及结果解读。抽样数量及结果判定见表2。从表2可以看出，随着群体规模增加，需要抽样量从1逐渐增加到9，而且所有检测个体均为抗体阳性时，则有95%以上把握认为该场内抗体合格率高于70%。

2.1.2当抽样检测为不完美试验时的抽样量及结果解读。抽样数量及结果判定见表3。从表3可以看出，随着群体规模增加，需要抽样量从1逐渐增加到32，而且当检测结果中抗体阴性个体数小于某个值时，则有95%以上把握认为该场内抗体合格率高于70%。例如群体大小为101头时，需要采样31头，当抗体阴性头数小于6头，也就是抗体阳性数高于25头以上时，可以有95%以上把握认为该场内抗体合格率高于70%。

2.2针对大群体抗体监测的抽样

当在大群体中抽样时，抽样比例不超过10%，此时抽样概率分布应使用二项分布进行计算。

2.2.1当抽样检测为完美试验时的抽样量及结果解读。抽样数量及结果判定见表4。从表4可以看出，群体规模在100头以上时，需要抽样量为9，当所有检测个体均为抗体阳性时，则有95%以上把握认为该场内抗体合格率高于70%。

2.2.2当抽样检测为不完美试验时的抽样量及结果解读。抽样数量及结果判定见表5。从表5可以看出，群体规模在200头以上时，需要抽样量为32，而检测阴性数少于6个，也就是阳性数量在26个以上时，则有95%以上把握认为该场内抗体合格率高于70%。

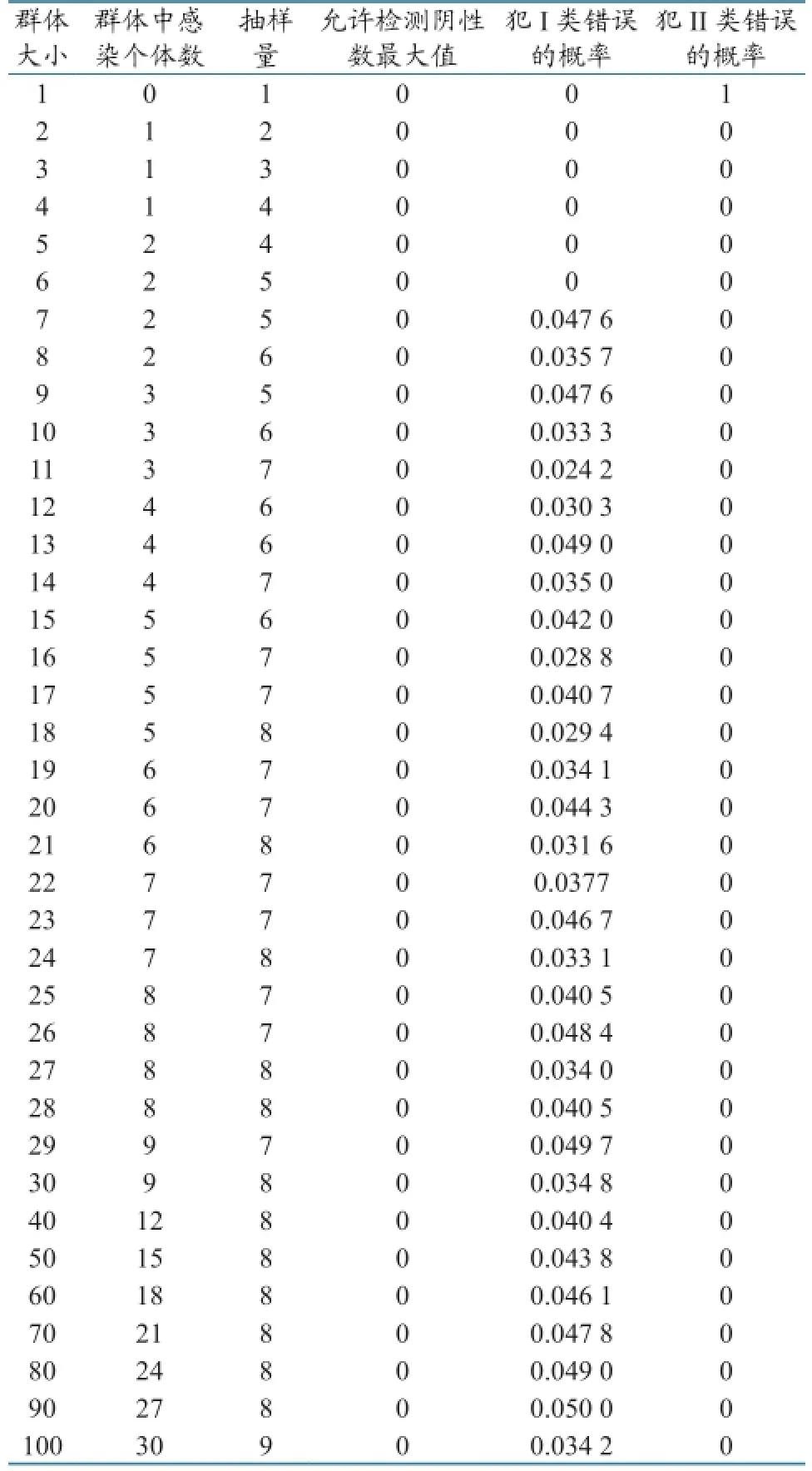
表2　对小群体使用完美检测方法时所需抽样量及结果判定

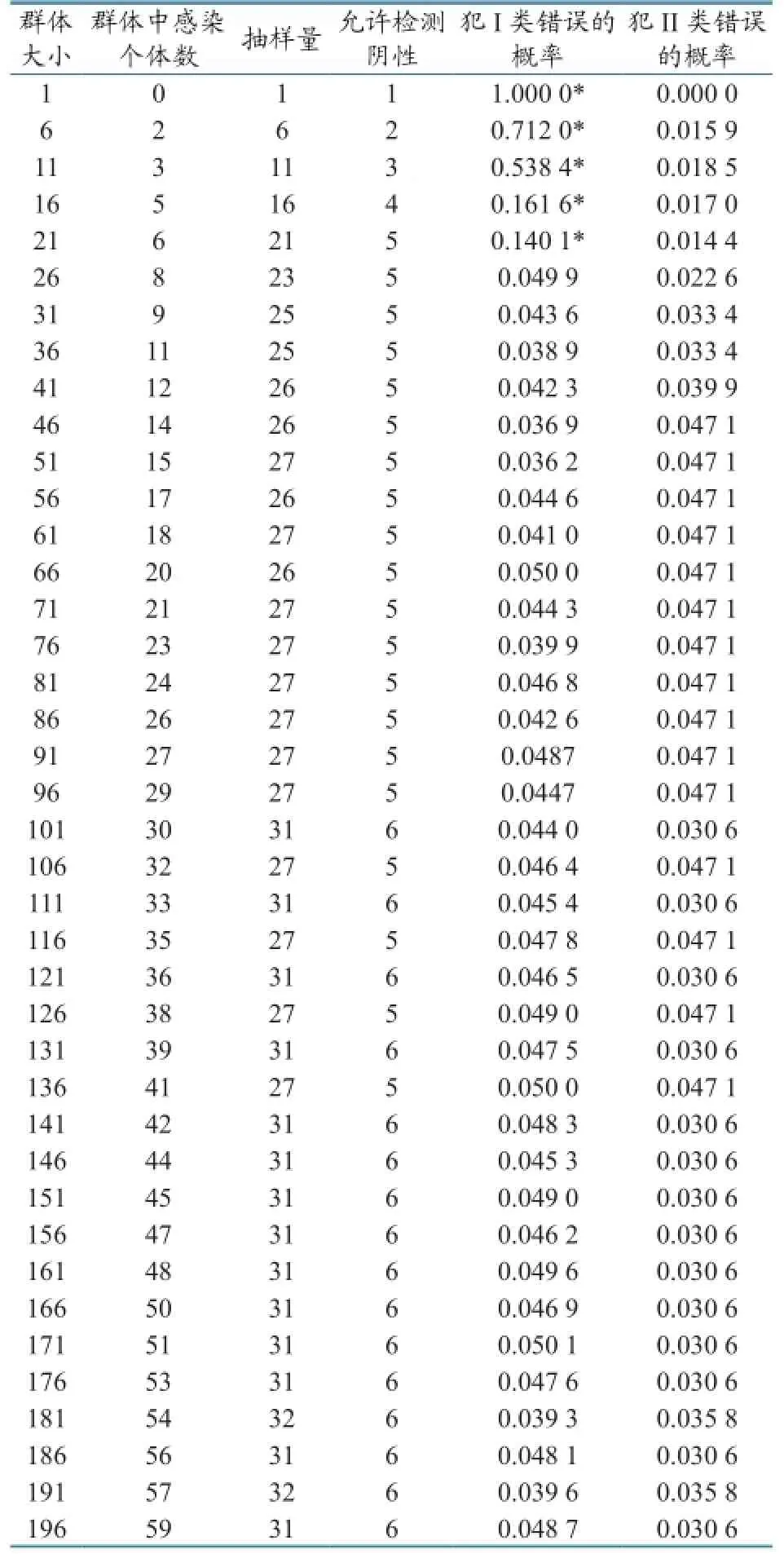
表3　对小群体使用不完美检测方法时所需抽样量及结果判定

3　讨论

目前我国对几种重大动物动物疫病实行强制免疫政策，而免疫后抗体监测通常被用来作为官方疫病控制部门免疫工作效果考核的重要指标。然而在生产实践中，抗体合格率除了受实际免疫的覆盖范围影响以外，还受其它多种因素影响。比如，疫苗的质量是否过关、疫苗运输储存的方式是否恰当、免疫动物的身体状况是否良好、抗体监测时采样是否合理以及血清是否正确处理和冷藏等。因此，在进行抗体监测的同时，应该收集必要的基础信息，进行必要的分析。抗体效价的评价不仅仅可以得到一个数值，更重要的是利用这个数值，分析免疫失败的原因，进一步改进免疫工作。这也是世界动物卫生组织（OIE）和国际粮农组织（FAO）所倡导的[9]。

本文通过对群体免疫理论及传染病传播动力学模型的介绍，分析了影响抗体合格率阈值大小的相关因素。根据传染病动力学原理，防止疫病流行所需要达到的免疫合格率水平受到多种因素的影响。我国地域广阔，不同地区的养殖方式和交易模式可能差别较大，而且不同规模场户交易频次和交易模式也不同，这些因素都可能导致相应要达到的免疫合格率不同。这也说明免疫不是控制疫病的唯一手段。此外，也可以通过制定政策，如引导交易前检疫、鼓励疫病净化等方式，减小感染场户与非感染场户的有效接触。需要说明的是，我国兽医流行病学刚刚起步，对于某种疫病流行病学参数的研究还很缺乏。例如：某地区某种动物养殖结构如何？不同类型场户地理上分布有何特点？不同类型的场户间动物交易模式？场户间交易频率是多少？建议进一步开展现场流行病学研究，探索不同地区养殖交易模式下的不同疫病传播模式，为当地制定科学合理的免疫策略提供基础。

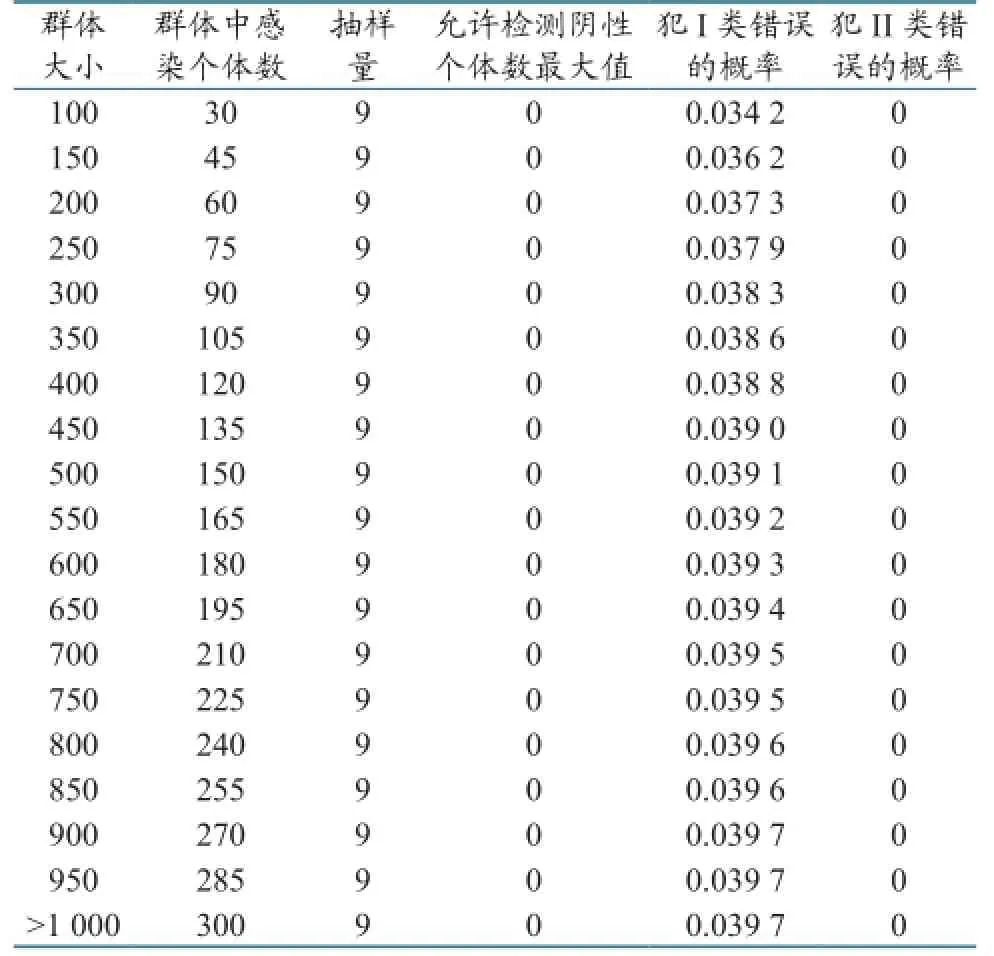
表4　对大群体使用完美检测方法时所需抽样量及结果判定

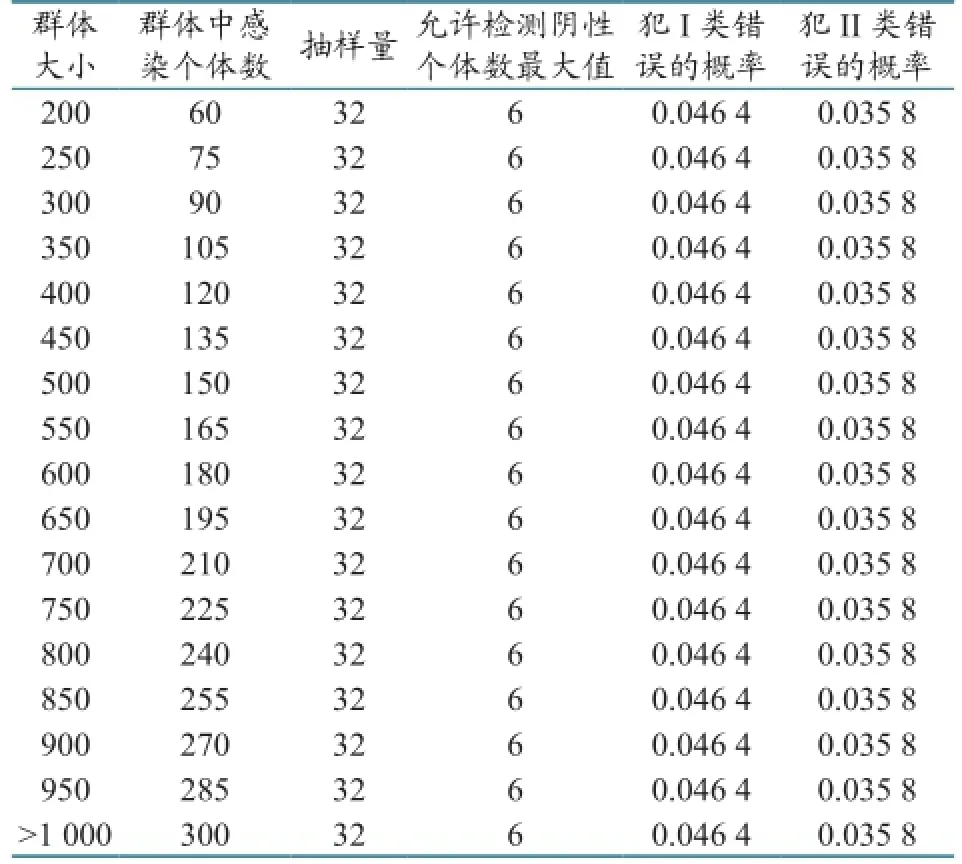
表5　对大群体使用不完美检测方法时所需抽样量及结果判定

[1]农业部兽医局. 2015年重大动物疫病强制免疫方案[A].北京：农业部，2015.

[2] 沈朝建，王幼明.兽医流行病学调查与监测：抽样技术手册[M]. 北京：中国农业出版社，2013.

[3] Hood G M. PopTools version 3.2.5. Available on the internet [Z/OL].（2011-09-22）[2016-06-30]. http://www.poptools.org.

[4] Fine P，Eames K， Heymann D L. “Herd immunity”：a rough guide，Clinical infectious diseases：an official publication of the Infectious Diseases[J]. Society of America，2011，52：911-916.

[5] Plans-Rubio P. The vaccination coverage required to establish herd immunity against influenza viruses[J]. Preventive medicine，2012，55：72-77.

[6] 马知恩，周义仓，王稳地，等. 传染病动力学的数学建模与研究[M]. 北京：科学出版社， 2004.

[7] Plans-RubioP.Is the current prevention strategy based on vaccination coverage and epidemiological surveillance sufficient to achieve measles and rubella elimination in Europe? [J]. Expert review of anti-infective therapy，2014，12：723-726.

[8] A.A.H. Services.Survey Toolbox for Livestock Diseases-A practical manual and software package for active surveillance of livestock diseases in developing countries[Z/OL][2016-06-30]. https://www.ausvet.com.au/.

[9] Food and Agriculture Organization of the United Nations（FAO）& World Organisation for Animal Health（OIE）. The Global Strategy for the Control and Eradication of PPR[Z]. Paris：FAO/OIE，2015.

（责任编辑：朱迪国）

Discussion and Calculation：Sampling Size and Interpretation of the Results in Serosurveillance

Li Yin，Zhang Meijing，Shen Chaojian，Sun Xiangdong，Kang Jingli，Huang Baoxu，Wang Youming
（China Animal Health and Epidemiology Center，Qingdao，Shandong266032）

In order to illuminate how to decide the sampling size and interpret the testing results during conducting antibody surveillance，so as to provide reference for practitioners，relevant epidemiological principles were introduced and debates about sampling size and result interpretation were analyzed and demonstrated systematically. Through necessary calculations，different ways of evaluating the immune qualification rate towards different scale livestock and poultry farms were put forward. The results indicated that the deficiencies of post-vaccination antibody surveillance still existed in China，and evidences on why the “70% coverage rate”was not suitable were given. This discussion and calculation would offer reference on how to further improve post-vaccination antibody surveillance in China.

veterinary epidemiology；serosurveillance；sampling；herd immunity；epidemic dynamics

S851.3

B

1005-944X（2016）12-0069-06

10.3969/j.issn.1005-944X.2016.12.020

科技部科技基础性专项“重要畜禽疫病流行病学调查”（2012FY111000）

王幼明