具有故障细胞的胚胎电子阵列上目标电路评估
朱赛, 蔡金燕, 孟亚峰, 李丹阳, 潘刚
(军械工程学院 电子与光学工程系, 河北 石家庄 050003)
具有故障细胞的胚胎电子阵列上目标电路评估
朱赛, 蔡金燕, 孟亚峰, 李丹阳, 潘刚
(军械工程学院 电子与光学工程系, 河北 石家庄 050003)
移除- 进化自修复通过进化自修复模式提高了目标电路的自修复能力,但在进化过程中,目标电路的评估尚缺少研究。在对胚胎电子阵列状态和目标电路形式数学描述的基础上,以马尔可夫不可修系统理论为指导,研究具有故障细胞的胚胎电子阵列上目标电路评估方法。研究了目标电路状态、状态转移率及工作状态概率自动计算方法,求解了目标电路可靠度及平均故障前时间,以此评估目标电路。仿真实验结果表明,该评估方法有效评估了进化过程中的目标电路形式,为移除- 进化自修复中目标电路的优选提供了理论参考依据。
系统评估与可行性分析; 胚胎电子阵列; 移除- 进化自修复; 可靠性评估; 马尔可夫不可修系统
0 引言
航空电子设备的工作环境恶劣、现场维修困难、故障后果严重,使得其对可靠性要求十分严格,而基于胚胎电子电路[1]实现的电子系统具有实时自修复能力,可大大提高航空电子设备的可靠性,在空天电子系统设计中具有广阔的应用前景[2-3]。
胚胎电子电路是一种新型的仿生硬件[4-6],其模拟多细胞生物的胚胎发育、修复过程,由结构相同的电子细胞排列为均匀的二维阵列,又称为胚胎电子阵列[7]。通过阵列中多细胞协作,执行目标电路功能,在自修复机制控制下,能够实时在线修复目标电路故障,实现目标电路的自修复[8- 9]。
移除- 进化自修复是一种新型的用于胚胎电子系统的自修复机制[10],既能够通过移除故障细胞进行目标电路的实时在线自修复,又能够通过进化优化目标电路结构,充分利用胚胎电子阵列中的细胞资源,提高目标电路的自修复能力。通过前端综合、逻辑优化映射、物理综合、基因库生成等[11-12],可以快速实现目标电路的进化。但在具有故障细胞的胚胎电子阵列上优化目标电路形式时,目标电路具有多种潜在的实现形式,如何择优选择使系统获得最大的自修复能力,尚缺少有效的评价方法。
可靠性是分析胚胎电子阵列及其修复策略的常用指标[13-14]。研究者结合胚胎电子阵列自修复特征,提出了多种自修复模型,但已有的可靠性模型没有考虑故障电子细胞对目标电路的影响[15],不适用于具有故障细胞的胚胎电子阵列上目标电路评估。
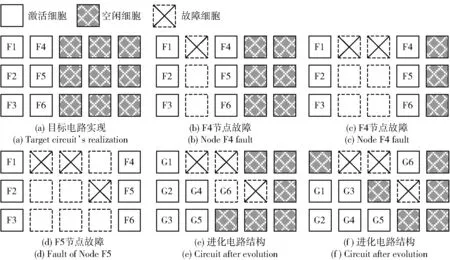
图1 移除- 进化自修复过程Fig.1 Elimination-evolution self-repair process
本文在分析移除- 进化自修复过程的基础上,利用马尔可夫不可修系统理论,研究了目标电路进化过程中目标电路的可靠性评估方法,并以其平均故障前时间(MTTF)为指标进行目标电路优选。该方法在胚胎电子阵列状态和目标电路实现的基础上,自动划分电路状态、求解状态间转移率,并计算目标电路的可靠度及MTTF,使用MTTF指标对进化过程中的不同电路形式进行评估,为目标电路的优选提供了理论依据。
1 胚胎电子阵列的移除- 进化自修复
1.1 移除- 进化自修复
胚胎电子阵列的移除- 进化自修复[10]包括移除自修复和进化自修复两种模式。移除自修复模式通过移除故障细胞所在行/列消除故障对目标电路的影响,实现自修复;进化自修复模式进化目标电路结构,“绕开”故障细胞以修复目标电路。系统运行过程中,根据目标电路的自修复能力自动选择修复模式:当阵列中存在冗余行/列资源时,通过移除自修复模式进行自修复;当阵列中冗余行/列资源不足以完成移除自修复时,进化目标电路结构提高目标电路的自修复能力,使电路重新获得修复能力,而后继续根据自修复能力选择修复模式,进行电路中故障的修复。
以某目标电路的自修复为例,其移除- 进化自修复过程如图1所示。初始状态下,胚胎电子阵列中所有细胞正常,目标电路的实现如图1(a)所示,其中F1~F6为目标电路的功能节点。当目标电路发生故障时,系统根据阵列中是否存在冗余列资源而采取相应的修复模式:当阵列中存在冗余列资源,能够支持列移除时,采用移除自修复模式通过列移除实时修复故障,当目标电路中F4、F4、F5功能节点分别依次发生故障时,其修复过程如图1(b)~图1(d)所示;随着自修复次数的增加,阵列中的冗余列不断减少,当冗余列数目降至0时,如图1(d)所示,无法继续采用列移除机制进行目标电路的修复。此时采用进化自修复模式,利用阵列中的正常电子细胞进化目标电路形式,得到具有相同功能、更适合具有故障细胞的胚胎电子阵列、具有较强自修复能力的电路形式,进化后的目标电路如图1(e)所示,G1~G6为进化后的功能节点。由图1(e)可以看出,进化后的目标电路重新拥有了冗余列,其自修复能力得到提高,可继续通过移除自修复模式修复后续故障。
由图1可以看出,移除- 进化自修复既保证了故障的实时自修复,又提高了系统的自修复能力。但在进化自修复模式中,同一目标电路功能存在多种实现形式,如图1(e)、图1(f)所示进化自修复中两种不同的目标电路形式。由于故障电子细胞的存在,使得冗余列对不同电子细胞的修复能力不同,如何选择电路实现形式使系统的自修复能力最大,需要有效的评估方法。
1.2 进化后的列移除分析
进化自修复模式所得目标电路在运行过程中,通过移除自修复模式进行修复。在修复过程中,电路状态的变化是随机的,且下一状态只与当前状态有关,与其他时刻状态无关,如图1(a)~图1(d)所示电路状态变化。在列移除过程中,以列为单位进行操作,其中每个激活细胞的故障都会导致整列的移除。
目标电路后一时刻状态只与当前状态有关,整个胚胎电子阵列上的目标电路是一个马尔可夫不可修系统。状态间的转移概率与目标电路中每列的可靠性相关,每列的可靠性由其中激活细胞的数目决定。进化后的目标电路在移除自修复过程中,符合马尔可夫系统特征,可使用马尔可夫不可修系统理论进行可靠性评估。
2 马尔可夫不可修系统及其可靠性
2.1 马尔可夫不可修系统
假设一个不可修系统有个N+1状态,记为E={0,1,…,N},其中状态0,1,…,K是系统的工作状态,记为W={0,1,…,K},K+1,K+2,…,N是故障状态,记为F={K+1,K+2,…,N}. 令X(t)表示时刻t该系统所处状态,若{X(t),t≥0}是时齐马尔可夫过程,即对任意自然数n及n个时刻0≤t1 p{X(tn)= in|X(t1)=i1,X(t2)=i2,…,X(tn-1)=in-1}= P{X(tn)=in|X(tn-1)=in-1}, i1,i2,…,in∈E, (1) 且对任意两个时刻t,u≥0,均有 p{X(t+u)=j|X(u)=i}=pij(t),i,j∈E (2) 与u无关,则该系统为马尔可夫不可修系统,可用马尔可夫系统理论求解其可靠性。 对于状态i,j∈E,函数pij(t)称为状态i到状态j的转移概率函数,p(t)=[pij(t)]称为转移概率矩阵。 对于上述马尔可夫不可修系统,一旦出现故障状态,则系统故障,即故障状态F中所有状态为系统的吸收态,一旦进入吸收态,系统就永远停留在该状态,则吸收态到其他状态的转移概率为0. 2.2 马尔可夫不可修系统的可靠度求解 对于具体系统,若其符合马尔可夫不可修系统特征,则可通过以下步骤分析其可靠性[18-19]: 1)定义系统状态,确定系统状态集E、工作状态集W及故障状态集F; 2)定义随机过程{X(t),t≥0}; 3)求状态转移率矩阵A,对于已定义的随机过程,首先求出 pij(Δt)=aijΔt+o(Δt),i≠j,i,j∈E, (3) 然后确定转移概率矩阵 A=[aij], (4) (5) 4)求时刻t各状态概率pj(t)=p{X(t)=j},j∈E. 在状态的初始分布(p0(0),p1(0),…,pN(0))已知的情况下,通过求解微分方程组 (p0(t),p1(t),…,pN(t))A (6) 可获得t时刻各状态概率。 故障状态F为吸收态,其转移到其他状态的概率为0,则(6)式可写为 (7) 式中:PW(t)=(p0(t),p1(t),…,pK(t))为正常状态概率;PF(t)=(pK+1(t),pK+2(t),…,pN(t))为故障状态概率;B是A左上角K+1行、K+1列子矩阵,是K+1个工作状态间的转移率矩阵。 则只需求 (8) 便可求出t时刻系统处于各工作状态的概率。 5)求系统可靠度函数和平均故障前时间 (9) (10) 首先对胚胎电子阵列和目标电路实现形式进行数学描述,在此基础上分析目标电路状态,并计算其状态间转移率,求解各工作状态概率分布,最终计算目标电路可靠度函数及平均故障前时间。 3.1 胚胎电子阵列的描述 为了进行目标电路的可靠性分析,首先确定阵列中故障细胞情况及目标电路的具体实现形式。对于规模为M×N,即由M行、N列电子细胞组成的胚胎电子阵列,定义状态矩阵和细胞使用矩阵进行胚胎电子阵列的描述,具体为: 1) 胚胎电子阵列的故障状态矩阵S=[sij]M×N,sij表示阵列中(i,j)位置细胞的状态,sij∈{0,1}:sij=1表示阵列中(i,j)位置的细胞故障;sij=0表示(i,j)位置的细胞正常; 2) 电子细胞工作状态矩阵Z=[zij]M×N:zij表示(i,j)位置上电子细胞的工作状态,zij∈{0,1}:zij=1表示(i,j)位置上电子细胞处于激活状态,执行目标电路功能;zij=0表示(i,j)位置上电子细胞处于空闲状态。Z代表了目标电路在胚胎电子阵列上的具体实现形式。 移除- 进化自修复中,进化后的电路在运行过程中采用行/列移除机制进行自修复,胚胎电子阵列和目标电路均为一列作为一个整体,因此下文中用S(i)表示矩阵S的第i列,用Z(j)表示矩阵Z的第j列。 胚胎电子阵列记为EA={1,2,…,i,…,N},其中1≤i≤N,代表阵列中的第i列细胞。 3.2 目标电路运行状态 目标电路状态包括正常工作状态和故障状态,正常工作状态下,目标电路所有列均由胚胎电子阵列上的列执行,电路能够完成正常功能。当胚胎电子阵列中剩余列不足以完成目标电路功能时,电路发生故障。 设目标电路规模为m×n,记目标电路每列功能在胚胎电子阵列上的实现位置为θ1、θ2、…、θn,其状态i记为Θi=(θ1,i,θ2,i,…,θj,i,…,θn,i),其中θj,i∈EA为胚胎电子阵列中执行目标电路第j列功能的列序号,且θ1,i<θ2,i<…<θj,i<…<θn,i. 目标电路的初始状态记为Θ0=(θ1,0,θ2,0,…,θn,0),sum(Z(θi,0))>0,即目标电路第i列功能所需电子细胞数目大于0. 为了完全分析目标电路的不同故障状态,在胚胎电子阵列的N列后增加n列“虚拟列”,每一“虚拟列”均能够执行电路中任意一列的功能。 由于阵列中存在故障细胞,因此阵列中的列与目标电路中的各列存在可实现问题,即阵列中的某列只能执行目标电路中某些列的功能,而对于其他列,由于存在故障细胞而无法实现。对于目标电路中的第i列和胚胎电子阵列中的第j列,若ZT(θi)·S(j)=0,则胚胎电子阵列的第j列能够执行目标电路的第i列功能;若ZT(θi)S(j)>0,则胚胎电子阵列的第j列不能执行目标电路的第i列功能。 定义可行性矩阵D=[dij]n×(N+n),dij∈{0,1}表示阵列中的第j列能否执行目标电路第i列功能,dij= 1时阵列中的第j列能执行目标电路第i列功能,否则,不能执行其功能。可行性矩阵D可由S、Z计算获得,其第i行中所有的1项即为θi的可选列范围,且D(i,1:θi,0-1)=0,D(i,N+1:N+n)=1,则使D(1,θ1)=1、D(2,θ2)=1、…、D(n,θn)=1,且1≤θ1<θ2<…<θn≤N+n的(θ1,θ2,…,θn)组合即为目标电路的状态。 由于移除自修复模式的存在,目标电路运行中自动选择可执行列执行目标电路功能,即目标电路不会因不可执行列而故障,只会因阵列无法实现目标电路功能导致目标电路使用了“虚拟列”而故障。因此满足θn≤N的为目标电路工作状态,θn>N的为故障状态。对于电路状态Θi,若θn,i≤N,目标电路所有列功能均能够由胚胎电子阵列实现,则其为工作状态;若θn,i>N,即目标电路中至少有一列功能无法由胚胎电子阵列完成而使用了“虚拟列”,则Θi为故障状态。基于以上分析,目标电路的工作状态集合为W={Θi|θn,i≤N},其中Θ0为目标电路初始状态,其故障状态集合为F={Θi|θn,i>N},目标电路所有状态集E={W,F}. 3.3 状态转移率计算 状态转移过程中,每一列在(t,t+Δt]中发生两次或两次以上转移的概率为o(Δt),即在Δt中,多列可能同时发生故障,一列最多只能发生一次故障。在胚胎电子阵列中,3列以上同时发生故障的概率非常小。因此,本文只考虑一列故障或两列同时故障,对于多于两列同时故障的情况,其转移率记为0. 对于任意两状态Θi,Θj∈E,Θi=(θ1,i,θ2,i,…,θn,i)、Θj=(θ1,j,θ2,j,…,θn,j),定义Θi到Θj的距离为Θi→j=(θ1,i→j,θ2,i→j,…,θn,i→j),其中 (11) 对θx,i、θx,j,(11)式中其减运算为 (12) 基于以上状态间距离定义,可进行状态间可转移判断:对于两状态Θi、Θj,若Θi到Θj的距离Θi→j中只包含0、1元素,则状态Θi可转移到Θj,否则,Θi不可转移到Θj. 胚胎电子阵列中,每个电子细胞的可靠度符合指数分布,即r(t)=e-λt. 目标电路第i列使用的电子细胞数目为sum(Z(θi,0)),则其可靠度函数为ri(t)=e-sum(Z(θi,0))λt,其故障率为λi=sum(Z(θi,0))·λ. 目标电路中第i、j列同时故障的故障率记为λi,j(t),有 (13) 若状态Θi可转移到Θj,则状态转移率为 (14) 若状态Θi不可转移到Θj,则其转移率aij(t)=0. 故障状态为吸收态,其转移到任意状态的概率为0,则可求出状态转移率矩阵A及其左上角K+1行、K+1列的子矩阵B为 (15) 3.4 可靠度及MTTF计算 设目标电路在t时刻处于工作状态Θi(0≤i≤K)的概率为pi(t),则将p(t)=(p0(t),p1(t),…,pK(t))代入(8)式,且p(0)=(1,0,…,0). 为便于求解,对代入p(t)后的(8)式作拉普拉斯变换,可得 (16) 对(16)式求解,通过拉普拉斯逆变换可得t时刻各状态概率p(t),则目标电路的可靠度函数为 R(t)=p(t)eK+1, (17) 式中:eK+1为K+1维的全1列向量。 根据(10)式可计算目标电路的MTTF. 为了详细阐述本文可靠性分析方法的具体应用过程,以文献[11-12]中目标电路为例,以其在具有故障细胞的胚胎电子阵列上具体实现的可靠性分析为例,详细阐述本文方法的计算过程;利用本文方法对其在正常胚胎电子阵列上的不同实现形式进行了可靠性分析,通过本文计算结果与分析结果的比较,验证了本文方法的有效性;对该电路进化过程中出现的多种形式进行了可靠性分析,以分析结果为依据,进行了目标电路形式的评估,说明了本文方法在进化自修复过程中的应用。 4.1 算例 文献[11-12]中目标电路在胚胎电子阵列上的实现如图2所示。为了便于说明目标电路运行状态,将胚胎电子阵列设置为3行5列,故障细胞数目、位置保持不变。 图2 目标电路的实现Fig.2 Implementation of target circuit 图2所示目标电路中,阵列中(1, 1)、(3, 2)位置的两个细胞故障,n13、n19、n18、n17、n23、n25为目标电路功能节点,(1, 3)细胞执行连接功能,也为激活细胞,则胚胎电子阵列的状态矩阵为 电子细胞工作状态矩阵为 胚胎电子阵列列数N=5,每列分别用1、2、3、4、5表示,目标电路列数n=3,每列分别用θ1、θ2、θ3表示,其中ZT(1)S(2)=1,即目标电路的第1列不能由胚胎电子阵列的第2列实现,则其可行性矩阵为 , 其中6、7、8列为“虚拟列”。 通过D上目标电路各列的组合,可以得到目标电路的各状态,具体如表1所示。 表1 电路运行状态 表1中W={0, 1, 2, 3, 4, 5, 6}为工作状态集,且状态0为初始状态;F={7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18}的各状态中出现“虚拟列”,胚胎电子阵列已无法支持目标电路正常运行,F为故障状态集。目标电路一旦进入故障状态则系统故障,停止运行,即故障状态为吸收态。 设阵列中每个细胞可靠度函数符合指数分布,即对每个细胞有r(t)=e-λt,则目标电路中θ1、θ2、θ3的可靠度分别为 r1(t)=e-2λt,r2(t)=e-2λt,r3(t)=e-3λt, 则目标电路中各列的故障率分别为 λ1=2λ,λ2=2λ,λ3=3λ. θ1、θ2两列同时故障的故障率记为λ1,2(t),θ1、θ3同时故障的故障率记为λ1,3(t),θ2、θ3同时故障的故障率记为λ2,3(t),则根据(13)式可得 记θ1、θ2、θ33列同时故障的故障率为λ1,2,3(t),由于3列同时故障的概率较小,本文不再考虑,令λ1,2,3(t)=0. 工作状态间的转移率矩阵B为 B= 式中:Λ=-(7λ+λ1,2(t)+λ2,3(t)+λ1,3(t)). 初始状态下,有p1(0)=1,p1(0) =p2(0) =p3(0) =p4(0) =p5(0) =p6(0) = 0,目标电路的可靠度函数为 (18) 经求解,各状态的概率及目标电路的可靠度变化如图3所示。 图3 各工作状态的概率变化Fig.3 Change in probability of operating states 则系统的平均故障前时间为 4.2 正常阵列上目标电路评估 本文方法也可用于正常阵列上目标电路的可靠性评估。对于文献[11-12]中目标电路,当胚胎电子阵列正常时,即其状态矩阵为 目标电路的两种不同实现形式分别为 由目标电路的实现矩阵可以看出,Z1中有3列冗余列,可以采用列移除机制修复3次故障,Z2中有2列冗余列,可以支持3次列移除自修复,很明显Z1实现优于Z2实现。采用本文方法分别计算以上两种实现形式的MTTF,结果为 MTTF1 = 8.67×105h, MTTF2= 6.35×105h. 可以看出,MTTF1>MTTF2,本文方法的计算结果与分析结果相吻合,可以证明本文方法的有效性。 4.3 故障阵列上目标电路评估 移除- 进化自修复方法的进化自修复过程中,对于部分故障的胚胎电子阵列,其目标电路形式是多样的。进化过程中,可通过本文方法求解目标电路每一种实现形式的MTTF,并以此为基础构建进化中个体电路的适应度函数。在适应度函数的引导下,逐步进化出更适应当前阵列、可靠度较高的目标电路形式。 对于4.1节中的目标电路,在进化过程中存在以下4种实现形式: 采用本文方法分别计算以上4个电路形式的MTTF,可得 MTTF1 = 4.50×105h, MTTF2 = 2.70×105h, MTTF3 = 2.42×105h, MTTF4 = 3.43×105h. 由计算结果可以看出,4种不同的电路形式中,均有两列冗余列,但不同的电路形式其可靠性不同,具有不同的MTTF,其中MTTF1>MTTF4>MTTF2>MTTF3,即Z1的MTTF最大。进化过程中,Z1对应的目标电路形式其适应度相较于其他3种实现形式最大,可根据适应度的不同做进一步的进化计算,最终进化出目标电路的最优实现形式。 在马尔可夫不可修系统理论的基础上,研究了具有故障细胞的胚胎电子阵列上目标电路的可靠性评估方法,从胚胎电子阵列状态和目标电路实现形式出发,研究了状态划分、转移率矩阵求解方法,在此基础上,给出了目标电路可靠性评估方法。 本文目标电路可靠性评估方法考虑了阵列中故障细胞对目标电路自修复的影响,能够精确计算出相同阵列状态下不同电路实现形式的可靠度。移除- 进化自修复方法的进化自修复模式下,针对进化过程中的每一个目标电路形式,可根据胚胎电子阵列状态和目标形式自动划分目标电路状态,计算转移率矩阵及求解各工作状态概率,最终计算目标电路可靠度函数及MTTF. 以目标电路的MTTF为依据设计进化过程中个体适应度函数,进而优选出具有较大可靠性的目标电路形式。 本文评估方法在胚胎电子阵列状态基础上,自动完成由目标电路实现形式到其MTTF的计算,适用于进化自修复应用环境,为移除- 进化自修复的进化自修复模式中目标电路形式的优选提供了理论依据。 References) [1] Samie M, Dragffy G, Tyrrell A M, et al. Novel bio-inspired approach for fault-tolerant VLSI systems[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2012, 21(10): 1878-1891. [2] 张砦, 王友仁. 基于可靠性优化的芯片自愈型硬件细胞阵列布局方法[J]. 航空学报, 2014, 35(12): 3392-3402. ZHANG Zhai, WANG You-ren. Method to reliability improving of chip self-healing hardware by array layout reformaticon[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3392-3402. (in Chinese) [3] 郝国峰, 王友仁, 张砦, 等. 可重构硬件芯片级故障定位与自主修复方法[J]. 电子学报, 2012, 40(2): 384-388. HAO Guo-feng, WANG You-ren, ZHANG Zhai, et al. In-chip fault localization and self-repairing method for reconfigurable hardware[J]. Acta Electronica Sinica, 2012, 40(2): 384-388. (in Chinese) [4] Yang I, Jung S H, Cho K H. Self-repairing digital system with unified recovery process inspired by endocrine cellular communication[J]. IEEE Transactions on Very Large Scale Integration Systems, 2013, 21(6): 1027-1040. [5] 李岳, 王南天, 钱彦岭. 原核细胞仿生自修复电路设计[J].国防科技大学学报, 2012, 34(3): 154-157. LI Yue, WANG Nan-tian, QIAN Yan-ling. Self-healing circuit design inspired by prokaryotic cell[J]. Journal of National University of Defense Technology, 2012, 34(3): 154-157.(in Chinese) [6] 徐佳庆, 窦勇, 吕启, 等. 电子组织: 一种具有自适应能力的可重构仿生硬件结构[J]. 计算机研究与发展, 2012, 49(9): 2005-2017. XU Jia-qing, DOU Yong, LYU Qi, et al. eTissue: an adaptive reconfigurable bio-inspired hardware architecture[J]. Journal of Computer Research and Development, 2012, 49(9): 2005-2017. (in Chinese) [7] Zhu S, Cai J Y, Meng Y F, et al. A novel structure of embryonics electronic cell array[J]. WSEAS Transactions on Circuits and Systems, 2014, 13: 224-232. [8] 王南天, 钱彦岭, 李岳, 等. 胚胎型在线自修复FIR滤波器研究[J]. 仪器仪表学报, 2012, 33(6): 1385-1391. WANG Nan-tian, QIAN Yan-ling, LI Yue, et al. Study of embryonic type on-line self-healing FIR filters[J]. Chinese Journal of Scientific Instrument, 2012, 33(6): 1385-1391. (in Chinese) [9] Bremner P, Liu Y, Samie M, et al. SABRE: a bio-inspired fault-tolerant electronic architecture[J]. Bioinspiration and Biomimetics, 2013, 8(1): 1-16. [10] 朱赛, 蔡金燕, 孟亚峰, 等. 具有进化能力的新型胚胎电子自修复系统[J]. 北京理工大学学报, 2015, 35(12): 1297-1302. ZHU Sai, CAI Jin-yan, MENG Ya-feng, et al. A novel embryonics self-repair system with evolutionary capacity[J]. Transactions of Beijing Institute of Technology, 2015, 35(12): 1297-1302. (in Chinese) [11] 朱赛, 蔡金燕, 孟亚峰. 一种LUT型胚胎电子阵列的功能分化方法[J]. 电子学报, 2015, 43(12): 2440-2448. ZHU Sai, CAI Jin-yan, MENG Ya-feng. A functional differentiation method for LUT-based embryonics array[J]. Acta Electronica Sinica, 2015, 43(12): 2440-2448. (in Chinese) [12] 朱赛, 蔡金燕, 孟亚峰, 等. 基于功能重分化的LUT型胚胎电子阵列进化自修复[J]. 微电子学与计算机, 2015, 32(9): 10-17. ZHU Sai, CAI Jin-yan, MENG Ya-feng, et al. An evolutional self-repair method based on re-differentiation for LUT-based embryonics array[J]. Microelectronics & Computer, 2015, 32(9): 10-17. (in Chinese) [13] 张砦, 王友仁. 基于可靠性分析的胚胎硬件容错策略选择方法[J]. 系统工程理论与实践, 2013, 33(1): 236-242. ZHANG Zhai, WANG You-ren. Guidelines to fault-tolerant strategy selection in embryonics hardware based on reliability analysis[J]. Systems Engineering-Theory & Practice, 2013, 33(1): 236-242. (in Chinese) [14] 朱赛, 蔡金燕, 孟亚峰, 等. 胚胎电子细胞中基因备份数目优选方法[J]. 北京航空航天大学学报, 2016, 42(2): 328-336. ZHU Sai, CAI Jin-yan, MENG Ya-feng, et al. Gene backup number selection method for embryonics cell[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 328-336. (in Chinese) [15] Zhang Z, Wang Y R. Method to self-repairing reconfiguration strategy selection of embryonic cellular array on reliability analysis[C]∥2014 NASA/ESA Conference on Adaptive Hardware and Systems. Leicester, UK: IEEE, 2014: 225-232. [16] 董学军, 武小悦, 陈英武. 基于Markov链互模拟的航天器发射任务可靠度模型[J]. 系统工程理论与实践, 2012, 32(10): 2323-2331. DONG Xue-jun, WU Xiao-yue, CHEN Ying-wu. Mission reliability model of spacecraft launch based on bisimulation of continuous-time Markov processes[J]. Systems Engineering - Theory & Practice, 2012, 32(10): 2323-2331. (in Chinese) [17] Yuan L, Meng X Y. Reliability analysis of a warm standby repairable system with priority in use[J]. Applied Mathematical Modelling, 2011, 35(9): 4295-4303. [18] Wang L Y, Cui L R. Aggregated semi-Markov repairable systems with history-dependent up and down states[J]. Mathematical and Computer Modelling, 2011, 53(5/6): 883-895. [19] 狄鹏, 黎放, 陈童. 考虑不同维修效果的多状态可修系统可靠性模型[J]. 兵工学报, 2014, 35(9): 1488-1494. DI Peng, LI Fang, CHEN Tong. Reliability model of multi-state repairable systems with different repair effects[J]. Acta Armamentarii, 2014, 35(9): 1488-1494. (in Chinese) Evaluation of Target Circuit Realized on Embryonics Array with Faulty Cells ZHU Sai, CAI Jin-yan, MENG Ya-feng, LI Dan-yang, PAN Gang (Department of Electronic and Optical Engineering, Ordnance Engineering College, Shijiazhuang 050003, Hebei, China) The elimination-evolution self-repair method can be used to increase the self-repairing capacity of target circuit by optimizing circuit structure. There has been little research on the target circuit evaluation in optimization process. Based on the mathematical description of embryonics array state and target circuit form, an evaluation method is proposed with Markov unrepairable system theory. The calculating method for state division, transition rate of state, and probability of working states is researched, and the reliability and mean time-to-failure of target circuit are calculated to evaluate the target circuit. The simulated and experimental results show that the proposed method can effectively evaluate the circuit forms in evolution process. system assessment and feasibility analysis; embryonics array; elimination-evolution self-repair; reliability evaluation; Markov unrepairable system 2016-04-05 国家自然科学基金项目(61372039、61601495) 朱赛(1987—),男,讲师。E-mail: szhumail@163.com V243.1 A 1000-1093(2016)11-2120-08 10.3969/j.issn.1000-1093.2016.11.021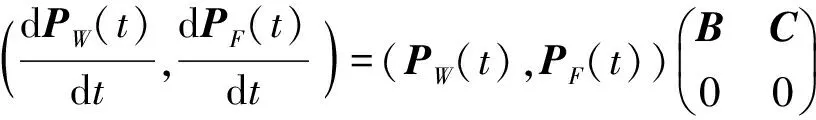
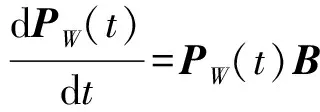
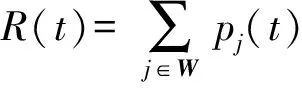
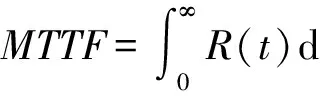
3 目标电路的可靠性分析
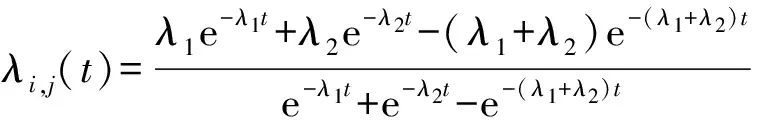
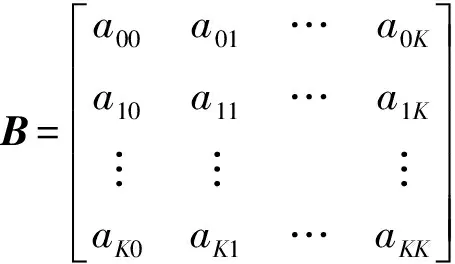
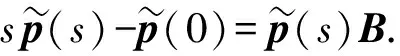
4 算例分析
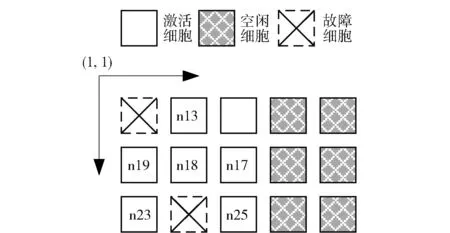

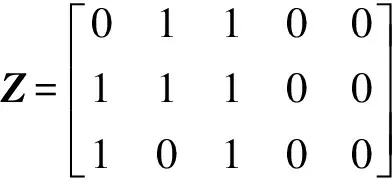

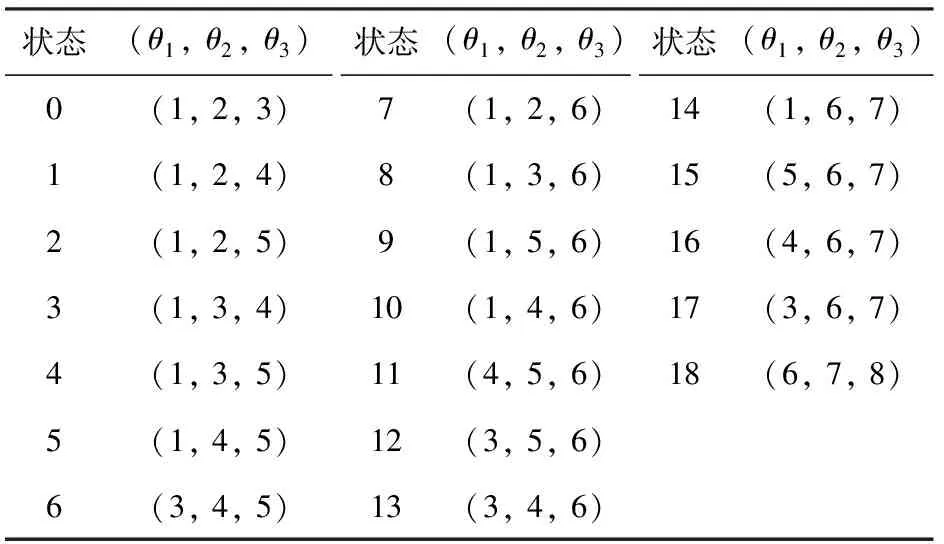
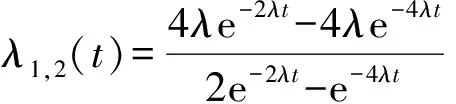
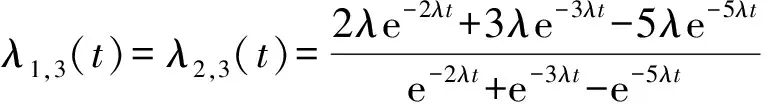

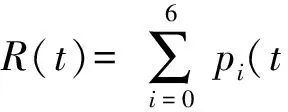
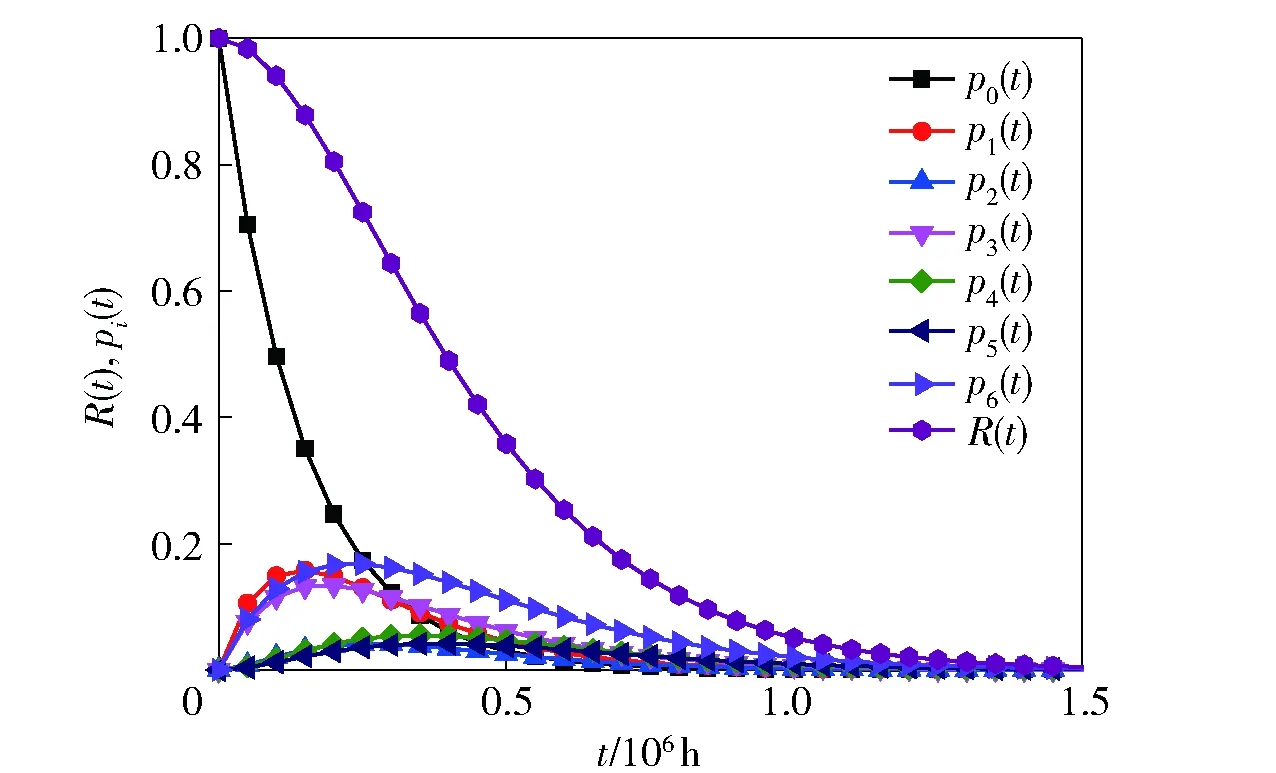
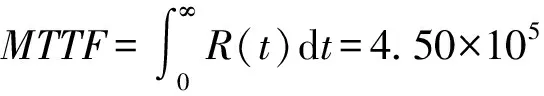
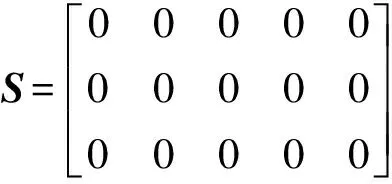
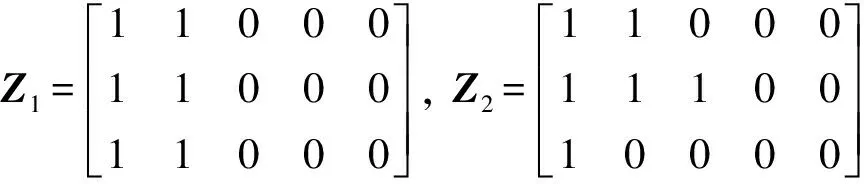
5 结论

