大口径火炮膛线结构对滑动弹带弹丸膛内运动影响的数值分析

许耀峰， 丁宏民， 徐坚， 宁变芳

(西北机电工程研究所， 陕西 咸阳 712099)



大口径火炮膛线结构对滑动弹带弹丸膛内运动影响的数值分析

许耀峰， 丁宏民， 徐坚， 宁变芳

(西北机电工程研究所， 陕西 咸阳 712099)

以大口径身管火炮发射减旋滑动弹带制导弹药时弹丸- 身管耦合系统为研究对象，基于弹塑性有限元理论，建立某大口径火炮线膛身管与制导炮弹耦合动力学有限元模型。数值计算了渐速膛线、等齐膛线、混合膛线(渐速膛线+等齐膛线)3种不同膛线形式和深、浅两种膛线深度条件下，制导炮弹在挤进阶段和膛内运动过程中的弹炮应力、挤进阻力以及弹炮动力学响应，获得了大口径火炮膛线结构对滑动弹带制导弹丸膛内运动的影响关系，为弹炮一体化设计提供了理论参考。

兵器科学与技术； 火炮膛线结构； 滑动弹带； 弹丸膛内运动； 有限元法

0 引言

制导弹药在针对特定点目标作战时，具有可以减少完成任务所需发射弹药数量、降低完成任务所需费用、减少附带损伤等显著优点。随着精确打击在战争中地位的不断提高，世界各军事强国在以大口径身管火炮为平台发射常规弹药的基础上，致力于发展可兼容发射的精确制导弹药。代表性的大口径制导弹药主要有美国的155 mm“铜斑蛇”激光末制导炮弹、“神剑”制导炮弹以及俄罗斯的152 mm“红土地”激光末制导炮弹等。

精确制导炮弹通常载有对发射过载相当敏感的电子测控、无线通信等制导器件，膛内最大过载不能超过制导器件可承受的过载上限，最小不能低于解脱引信保险所需要的过载下限；为减小电子器件受到的旋转加速度通常采用刚强度受限的减旋滑动弹带，弹丸挤进过程弹带滑动环不能受损，膛内运动过程中滑动弹带须能可靠正常工作。滑动弹带制导炮弹受到的挤进阻力和膛内过载与弹丸结构、身管内膛结构、弹炮匹配间隙等诸多因素有关，其中与火炮膛线结构有着密切关系。

国内外对制导炮弹发射过程中的动力学进行了相关研究，例如：朱兵[1]建立了末制导炮弹电子系统有限元仿真模型，对发射过程中弹体的动力学特性进行了有限元仿真，给出了弹体在冲击响应下的过载、等效应力、电路板变形等计算结果；张振辉等[2]分析了末制导炮弹膛内过载影响因素，建立了末制导炮弹与火炮身管相互耦合的动力学仿真模型，对末制导炮弹膛内过载进行了数值仿真；Cordes等[3-4]通过有限元分析及试验手段对“Excalibur”制导炮弹过载承受能力进行了验证，分析了引起末制导炮弹过载幅值突然变化的影响因素；孙河洋等[5]考虑了经典内弹道方程组和弹带挤进过程的耦合效应，分析了坡膛结构变化对火炮内弹道性能的影响；曾志银等[6]建立了弹丸身管耦合系统非线性有限元分析模型，分析了弹丸挤进过程中膛线起始段的应力应变；马明迪等[7]基于有限元与光滑粒子耦合算法，建立了弹丸身管耦合系统动力学模型，弥补了弹丸挤进过程有限元分析方法无法有效模拟弹带大变形的缺陷；刘雷等[8]、葛建立等[9]建立了基于接触理论的弹丸身管耦合动力学模型，仿真计算了弹丸膛内运动过程；孙全兆等[10]建立了弹带挤进坡膛的有限元模型，数值模拟研究了弹带的动态挤进过程，计算得到弹带挤进阻力、挤进压力和弹丸运动规律。国内外鲜见有关火炮膛线结构对滑动弹带制导炮弹膛内运动影响的公开报道。

本文基于弹塑性有限元理论，建立了某大口径火炮线膛身管与末制导炮弹耦合动力学有限元模型，数值计算了不同膛线结构时末制导炮弹在挤进、膛内运动过程中的弹炮应力、挤进阻力以及弹炮动力学响应，分析了大口径火炮膛线结构对滑动弹带制导炮弹膛内运动的影响。

1 弹炮耦合动力学有限元模型

1.1 有限元模型

以某大口径火炮身管和末制导炮弹耦合系统为研究对象，建立了渐速膛线、等齐膛线、混合膛线(渐速膛线+等齐膛线)身管以及末制导炮弹三维几何模型。应用ANSYS/LS-DYNA显式动力学分析软件建立有限元模型，身管、弹体、滑动环采用solid164六面体拉格朗日单元进行网格划分，对膛线起始部进行了网格加密，弹带采用无网格光滑粒子流体动力(SPH)算法进行计算。有限元模型中弹带SPH粒子与滑动环之间无相对运动，采用点- 面绑定接触、弹带粒子与身管内壁之间定义为自动点- 面接触，滑动环与弹体之间、弹体前后定心与身管内壁之间定义为自动面- 面接触。自动点- 面及面- 面接触采用罚函数法进行计算，计算中每一迭代步检查从节点是否穿透主表面，如果没有穿透不做任何处理，否则在该从节点与被穿透的主表面间引入一个大小与穿透量及主表面单元刚度成正比的接触力。这种处理方法相当于在从节点与被穿透的主表面之间设置一个法向弹簧，以限制从节点对主表面的穿透。

图1为身管膛线起始部有限元网格，图2为末制导炮弹有限元网格，图3为末制导炮弹局部结构。

图1 不同膛线有限元网格局部图Fig.1 Finite element meshes of different riflings

图2 滑动弹带末制导炮弹有限元网格Fig.2 Finite element meshes of terminal guided munition with sliding driving band

图3 滑动弹带结构Fig.3 Partial structure of sliding driving band

1.2 材料模型

身管材料为PCrNi3MoVA，滑动环材料为35CrMnSi，均采用双线性模型。弹带材料为紫铜，弹带采用如(1)式所示塑性随动强化模型：

(1)

(2)

Et为切向模量，E为杨氏模量。

1.3 载荷和边界条件

在本文的研究中，重力载荷作为常力直接加载在模型中，采用1号装药的内弹道参数、按弹底压力- 时间曲线将压力施加到弹带后部所有作用面上，以模拟火药气体对弹丸的作用。考虑到膛内时期炮身后坐对发射过程的影响程度较小，因此简化数值计算模型，忽略炮身后坐，约束身管尾端面3个方向自由度，定义摇架前后铜衬套与身管圆柱部的接触/碰撞。

2 末制导炮弹挤进及膛内运动数值计算

2.1 计算条件

按照以下4种情况进行计算，对比不同火炮膛线结构发射末制导炮弹时的弹炮运动学、动力学响应：

1)膛线形式为渐速膛线，深2.30 mm；

2)膛线形式为等齐膛线，深2.30 mm；

3)膛线形式为混合膛线，深2.30 mm；

4)膛线形式为等齐膛线，深1.27 mm.

各计算条件中身管及弹带结构均取设计名义尺寸，弹体定心部取公差下限中值，初始装填角度均为0°.

2.2 数值计算结果

图4 不同时刻身管等效应力分布图Fig.4 Equivalent stress distribution of barrelat different times

首先数值模拟对比了不同膛线形式(渐速膛线、等齐膛线、混合膛线)发射末制导炮弹时的弹炮动力学、运动学响应，膛线深度均为2.30 mm. 图4、图5、图6分别给出了渐速膛线时的弹丸挤进及膛内过程中不同时刻的身管、弹带及滑动环等效应力分布。混合膛线起始部膛线形式与渐速膛线完全相同[11-12]，只是在炮口段为等齐膛线，因而混合膛线时的弹丸挤进及膛内过程中(不含炮口段)不同时刻的身管、弹带及滑动环等效应力分布与渐速膛线的相同；等齐膛线时的等效应力分布与图4、图5、图6类似，只是量值不同。

图5 不同时刻弹带等效应力分布图Fig.5 Equivalent stress distribution of band at different times

图7为渐速膛线、等齐膛线及混合膛线(膛线深度均为2.30 mm)的弹丸挤进阻力对比曲线，图8为不同膛线形式(膛线深度均为2.30 mm)时弹丸弹体前定心部与身管碰撞引起的身管等效应力曲线。 表1列出了不同膛线形式(膛线深度均为2.30 mm)时的弹炮应力、挤进阻力的最大幅值

图6 不同时刻滑动环等效应力分布图Fig.6 Equivalent stress distribution of slide ring at different times

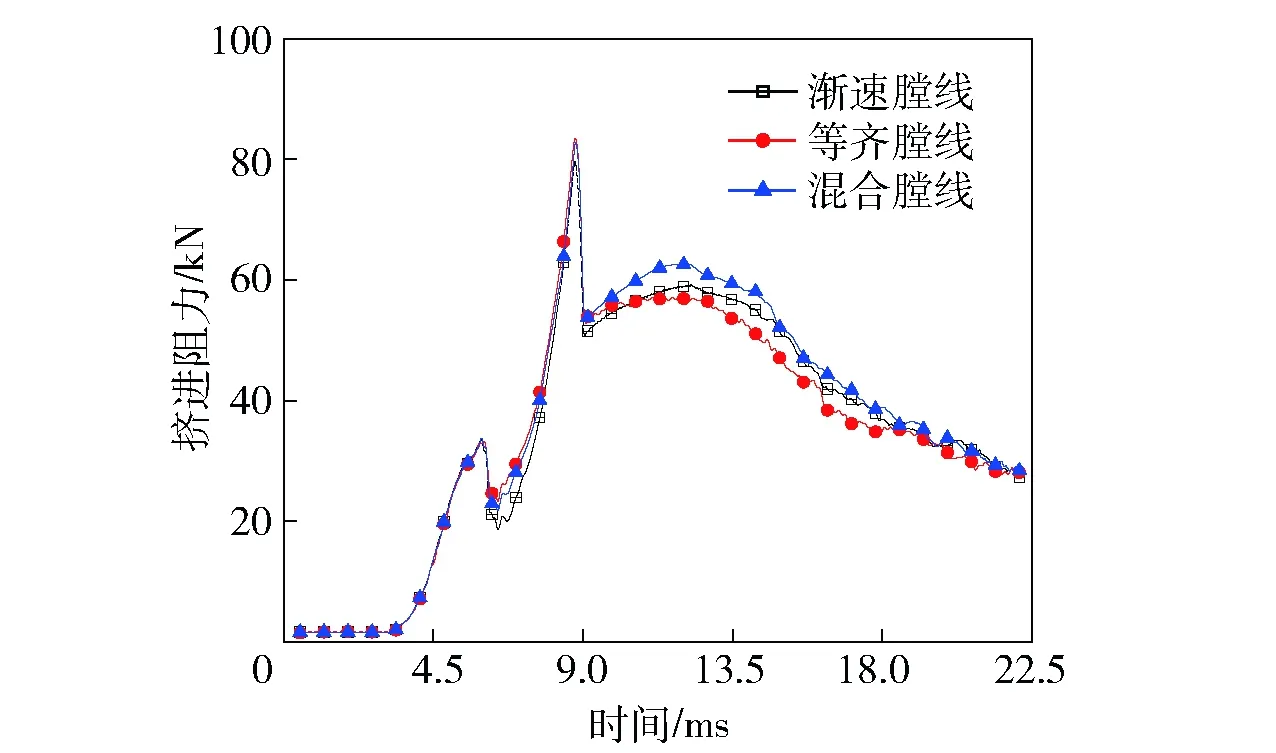
图7 不同膛线形式弹丸挤进阻力曲线Fig.7 Squeezing resistance curves of projectiles with different riflings

膛线形式挤进时身管阳线应力/MPa直膛运动时身管阳线应力/MPa弹带应力/MPa滑动环应力/MPa弹炮碰撞时的身管等效应力/MPa挤进阻力/kN渐速膛线69859061411911188811等齐膛线82968262713161209857混合膛线69859061411911219843

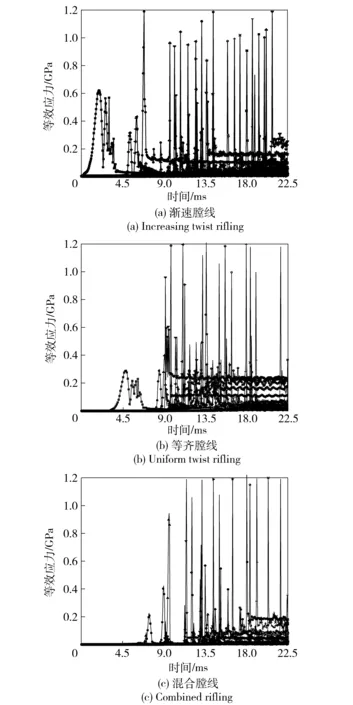
图8 不同膛线形式弹炮接触碰撞时的身管等效应力Fig.8 Equivalent stress curves of barrels with different riflings during projectile-barrel contacting and impacting

图9、图10、图11为弹丸膛内运动时特征点的位移、速度、加速度、角加速度响应曲线，表2列出了不同膛线形式时的弹丸膛内运动时特征点的位移、速度、加速度、角加速度最大幅值，膛线深度均为2.30 mm.

图9 不同膛线形式弹丸头部中心点横向位移、 速度曲线对比Fig.9 Transverse displacement and velocity in the center of projectile head

图10 不同膛线形式控制舱质心加速度曲线对比Fig.10 Acceleration curves of centroid of control cabin for different riflings

以上数值计算对比了不同膛线形式发射末制导炮弹时的弹炮动力学、运动学响应。下面进一步对比采用等齐膛线、但膛线深度不同(深膛线深度2.30 mm，浅膛线深度1.27 mm)时发射末制导炮弹的弹炮动力学、运动学响应。图12为深、浅膛线的弹丸挤进阻力对比曲线，图13～图16分别为深、浅膛线弹丸膛内运动时特征点的位移、速度、加速度、角加速度响应曲线。表3列出了深、浅膛线时的弹、炮应力、挤进阻力的最大幅值，表4列出了深、浅膛线时的弹丸膛内运动时特征点的位移、速度、加速度、角加速度最大幅值。

3 数值计算结果分析

从图4～图6弹丸挤进和膛内运动过程中身管、弹带、滑动环等效应力分布以及表1可以看出，由于起始缠角不同，等齐膛线时弹丸挤进及膛内运动中身管、弹带、滑动环等效应力高于渐速膛线、混合膛线时的等效应力，但小于材料屈服极限。

由表3可以看出，由于弹带与身管阳线之间过盈量不同，深膛线时弹丸挤进及膛内运动中身管、弹

带、滑动环等效应力均高于浅膛线时的等效应力，深膛线时身管阳线等效应力最大为829 MPa，而滑动环的等效应力最大值达到1 316 MPa，接近材料屈服极限。

图11 不同膛线形式弹丸角加速度曲线Fig.11 Angular acceleration curve of projectile for different riflings

表2 不同膛线形式弹丸运动响应最大幅值

表3 深、浅膛线时弹炮应力、挤进阻力最大幅值

表4 深、浅膛线时弹丸运动响应最大幅值

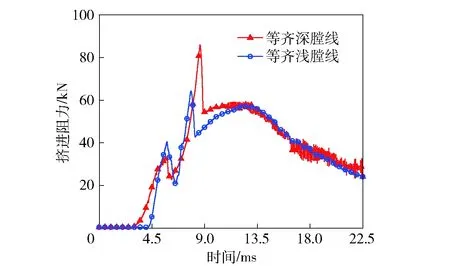
图12 等齐深、浅膛线弹丸挤进阻力曲线对比Fig.12 Squeezing resistance curvess of projectiles for different depths of uniform twist rifling

图13 等齐深、浅膛线弹头中心节点横向位移Fig.13 Transverse displacement curves of projectile head for different depths of uniform twist rifling

图14 等齐深、浅膛线弹头中心节点横向速度Fig.14 Transverse velocity curves of projectile head for different depths of uniform twist rifling

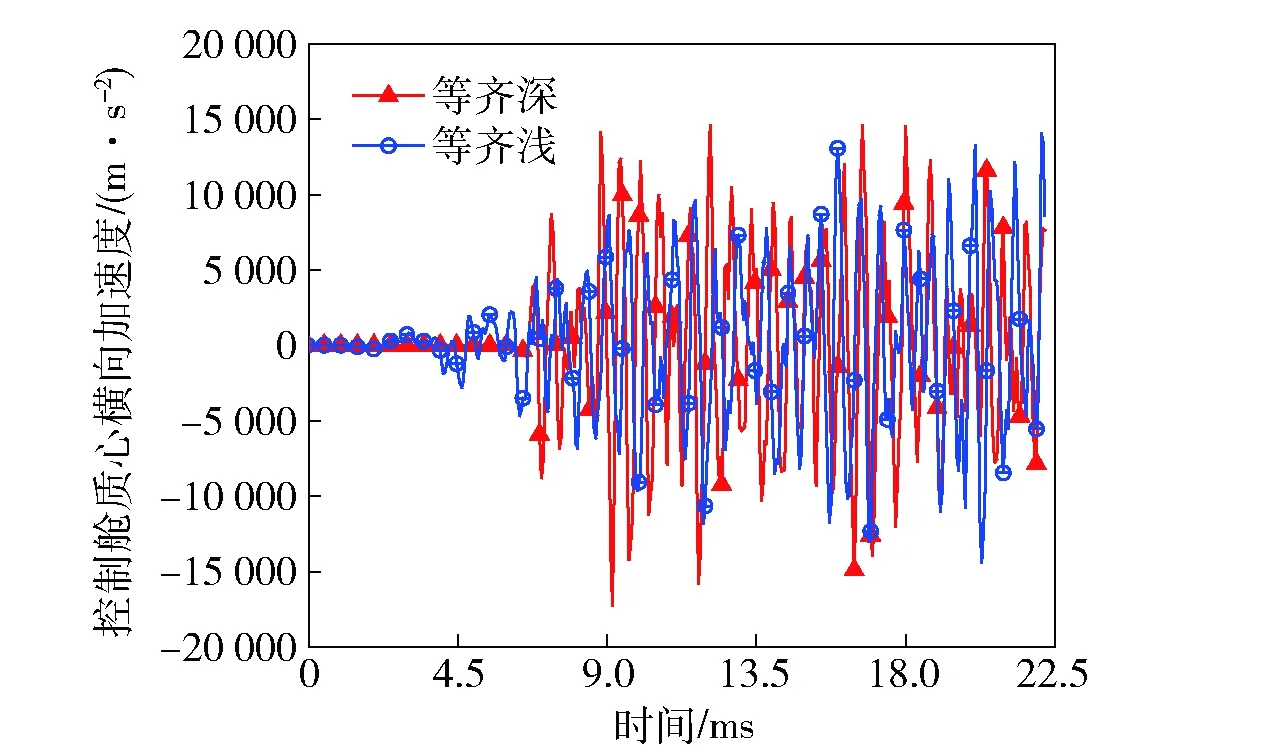
图15 等齐深、浅膛线控制舱质心横向加速度Fig.15 Transverse acceleration curves of centroid of control cabin for different depths of uniform twist rifling

图16 不同膛线深度时弹丸角加速度曲线Fig.16 Angular acceleration curves of projectile for different depths of rifling

从图7弹丸挤进阻力对比曲线可以看出，不同膛线形式时的挤进阻力曲线变化规律相同，只是幅值稍有差异。浅膛线时弹带与身管阳线之间过盈量较小，弹丸挤进阻力也小，从图12可以看出，等齐浅膛线最大挤进阻力为64.1 kN，等齐深膛线为85.7 kN.

从图8及表1、表3数据看出，不同膛线形式时弹丸定心部与身管碰撞引起的身管等效应力基本在1 200 MPa左右，小于身管材料屈服极限。

从弹丸运动响应对比曲线看出，计算给出的弹丸特征点运动响应均存在高频振动特征，这是由于弹丸在做刚体运动的同时还存在自身的固有振动引起。由曲线和表2、表4数据可以看出，不同膛线形式、不同膛线深度时弹丸膛内运动中的弹丸轴向位移、速度及加速度均接近，轴向最大过载不到7 000g，未超过该末制导炮弹轴向最大允许过载10 000g；在弹丸横向运动响应方面，渐速膛线、等齐膛线时弹丸最大横向过载在1 700g左右，混合膛线时的弹丸最大横向过载为1 400g；渐速、混合膛线时的弹丸旋转角加速度随时间逐渐增大，渐速膛线时的最大幅值为10 422 rad/s2左右，而等齐膛线时的角加速度明显小于前二者，最大幅值只有7 731 rad/s2，较渐速膛线减小26%；等齐深膛线时的弹丸旋转角加速度较等齐浅膛线小。

4 结论

本文应用弹塑性有限元理论，建立了大口径火炮某线膛身管与滑动弹带末制导炮弹耦合动力学有限元模型，采用数值计算研究了特定装填及装药条件下不同膛线结构对制导弹药膛内运动的影响，通过分析得出了以下结论：

1)深膛线时身管、弹带、滑动环的等效应力以及弹丸挤进阻力高于浅膛线。滑动弹带制导炮弹挤进和膛内运动过程中，深膛线时的滑动环最大等效应力接近材料屈服极限，可能引起滑动环变形，使滑动环与弹体卡滞，影响滑动弹带减旋效果或弹丸膛内正常运动，还可能导致弹带与身管阴线形成径向间隙，影响弹带闭气性能，导致机构受损或不能可靠工作。

2)渐速膛线、等齐膛线和混合膛线 3种膛线形式对弹丸膛内运动的轴向过载影响不大，弹丸横向过载处于同一数量级，幅值不大，未超过该末制导炮弹轴向最大允许过载。

3)不同膛线结构对弹丸转动过载影响不同。渐速膛线时的弹丸旋转角加速度幅值最大，混合膛线次之，而等齐膛线时的角加速度最小；深膛线时的弹丸旋转角加速度相较浅膛线幅值要小。

根据本研究方法建立的身管与固定弹带弹丸动力学模型，数值计算弹丸膛内纵向、横向过载数值与试验测试结果相符度较好，后续需要对滑动弹带弹丸膛内运动进行试验测试验证。不同膛线结构对固定弹带、滑动弹带弹丸膛内运动的影响，对身管火炮兼容发射精确打击弹药的技术研究至关重要，本文的研究成果对大口径火炮弹炮一体化设计具有一定的参考价值。

References)

[1] 朱兵. 制导炮弹电子系统冲击动力学研究[D]. 长沙:国防科学技术大学, 2010. ZHU Bing．Impact dynamic analysis of electronic system of guided munition[D]．Changsha：Defence Science University, 2010.(in Chinese)

[2] 张振辉，杨国来，葛建立．末制导炮弹膛内过载影响因素数值分析[J]．四川兵工学报, 2012,33(9):33-35. ZHANG Zhen-hui, YANG Guo-lai, GE Jian-li．Influnce factor analysis of terminal guided munition overload in bore[J]. Journal of Sichuan Ordnance, 2012,33(9):33-35.(in Chinese)

[3] Cordes J, Vega J, Carlucci D E, et al. Design accelerations for the army’s excalibur projectile, ADA435761[R]. NJ, US:Army Armament Research Development and Engineering Center, 2006.

[4] Cordes J, Vega J , Carlucci D E, et al. Structural loading statistics of live gun firings for the army’s excalibur projectile, ADA431877[R]. NJ, US:Army Armament Research Development and Engineering Center, 2005.

[5] 孙河洋, 马吉胜, 李伟, 等. 坡膛结构变化对火炮内弹道性能影响的研究[J]. 兵工学报, 2012, 33(6):669-675. SUN He-yang, MA Ji-sheng, LI Wei, et al. Study on influence of bore structure on gun’s interior ballistic performances[J]．Acta Armamentarii, 2012, 33(6): 669-675.(in Chinese)

[6] 曾志银, 马明迪, 宁变芳, 等. 火炮身管阳线损伤机理分析[J]. 兵工学报, 2014, 35(11):1736-1742. ZENG Zhi-yin, MA Ming-di, NING Bian-fang, et al. Analysis of rifling land damage mechanism of gun barrel[J]．Acta Armamentarii, 2014, 35(11): 1736-1742.(in Chinese)

[7] 马明迪, 崔万善, 曾志银, et al. 基于有限元与光滑粒子耦合的弹丸挤进过程分析[J]. 振动与冲击, 2015, 34(6):146-150. MA Ming-di, CUI Wan-shan, ZENG Zhi-yin, et al. Analysis of engraving process of projectile based on the coupling of FEM and SPH[J]．Journal of Vibration and Shock, 2015, 34(6):146-150. (in Chinese)

[8] 刘雷, 陈运生, 杨国来. 基于接触模型的弹炮耦合问题研究[J]. 兵工学报, 2006, 27(6):984-987. LIU Lei, CHEN Yun-sheng, YANG Guo-lai．A study on the projectile-barrel coupling based on contact model[J]. Acta Armamentarii, 2006, 27(6):984-987.(in Chinese)

[9] 葛建立, 杨国来, 陈运生, 等. 基于弹塑性接触/碰撞模型的弹炮耦合问题研究[J]. 弹道学报, 2008, 20(3):103-106. GE Jian-li, YANG Guo-lai, CHEN Yun-sheng, et al．A study on the projectile-barrel coupling based on contact model[J]. Journal of Ballistics, 2008, 20(3):103-106.(in Chinese)

[10] 孙全兆, 杨国来, 王鹏, 等. 某大口径榴弹炮弹带挤进过程数值模拟研究[J]. 兵工学报, 2015, 36(2):206-213. SUN Quan-zhao, YANG Guo-lai, WANG Peng, et al. Numerical research on rotating band engraving process of a large-caliber howitzer[J]．Acta Armamentarii, 2015, 36(2): 206-213.(in Chinese)

[11] 谈乐斌, 张相炎, 管红根, 等. 火炮概论[M]. 北京:北京理工大学出版社, 2005. TAN Le-bin, ZHANG Xiang-yan, GUAN Hong-gen, et al. Gun introduction[M]. Beijing:Beijing Institute of Technology Press, 2005.(in Chinese)

[12] 张相炎. 火炮设计理论[M]. 北京:北京理工大学出版社, 2005. ZHANG Xiang-yan. Theory of gun design[M]. Beijing:Beijing Institute of Technology Press, 2005.(in Chinese)

Numerical Analysis of Influence of Rifling Structure of Large Caliber Gun on Moving of Projectile with Sliding Driving Band in Bore

XU Yao-feng， DING Hong-min， XU Jian， NING Bian-fang

(Northwest Institute of Mechanical and Electrical Engineering， Xianyang 712099， Shaanxi， China)

A projectile-barrel coupled system of large caliber gun for launching a guided projectile with sliding driving band is studied. A guided projectile-barrel coupled dynamic finite element model of some large caliber gun is established based on elastic and plastic finite element theory. The projectile stress, squeezing resistance, and dynamic response between projectile and barrel in the process of projectile squeezing into rifling grooves and the process of straight moving of guided projectile in bore considering increased twist rifling, uniform twist rifling and increasing-uniform combined rifling, as well as deep rifling and shallow rifling are calculated. The relationship between the rifling structure of large caliber gun and the motion of guided projectile in bore is obtained.

ordnance science and technology; gun rifling structure; sliding driving band; projectile moving in bore; finite element method

2015-11-12

国防“973”计划项目(51319704)

许耀峰(1962—)，男，研究员级高级工程师。E-mail: 2211659128@qq.com

TJ302

A

1000-1093(2016)11-2148-09

10.3969/j.issn.1000-1093.2016.11.024