高中物理习题教学中的图象转换策略
金毅 袁海泉


1 剖析“图象转换策略”
在中学的物理学习过程中,学生会接触到大量函数图象,例如v-t图象和x-t图象,它们是对客观物理量的一种表示.这些函数图象不仅描述了因变量随自变量变化而变化的关系,而且由于物理量之间的逻辑关联,图象之间还存在着因果关系.在解决某些特定物理问题时,我们将物理量的函数图象作为条件,根据已知的公理、定理等经过演算和逻辑推理得到目标物理量的函数图象,在这一过程我们利用的思想方法将其称为“图象转换法”.那么“图象转换法”的本质是什么呢?实际上,图象转换法就是函数图象思想与转化思想的有机结合.这一思维方法不仅以物理规律和定律为基础,利用函数概念和性质去分析和转化问题,并且用图象这种具体和形象的数学语言作为工具,描述物理量的变化,从而解决问题.
在中学物理教学和学习中,“图象转换策略”常运用在纯运算无法完全解决的物理问题中,借助物理图象辅助定性呈现物理过程的变化,提高解决问题的效率和准确性.主要的应用流程如图1所示:
在解决与函数图象有关的问题时,首先要明确已知条件量与目标量之间的物理逻辑关系:“是线性关系还是非线性关系?有没有具体的定理明确两者的关系?”然后要根据条件图象的特点建立与目标图象的关系,例如条件图象的斜率,面积,交点等来决定用何种数学方法分析,例如求导,积分,建立函数关系等等.接下来,根据以上分析结论定性地绘制目标图象,其中在遇到临界点和拐点等特殊情况时需要特别注意,判断其对目标量变化趋势的影响.最后,根据所求得出结论,问题得到解决.
图象作为物理量的实际表征,它的生成过程是将具体的物理过程抽象成函数之后再转化为函数图象.它是将物理变化由具体转化为抽象再由抽象转化为形象图表的过程,其对于培养学习者的抽象思维和数形结合思想有着极其重要的意义.教师运用图象转换的策略,不仅可以直观呈现物理问题,提高解决问题的效率,而且可以帮助学生通过视觉表征的形式记忆和提炼学习结果,实现教学形式与教学方法的最优化.图象转换实际上是函数思想和转化思想的结合,将数学与物理密切联系,是帮助学生开发和锻炼思维,熟练运用所学知识解决问题的良好手段.
2 匀变速直线运动问题的图象转换
匀变速问题是高中物理运动学中重要的部分,在这一专题中主要涉及的是v-t图象和x-t图象.某对象的v-t图象的斜率表示加速度a,其v-t图象与坐标轴围成的面积表示相应时间的位移x,这与它的x-t图象正是一种积分关系.相反,x-t图象的斜率就是表示该时刻的速度v,与v-t图象是微分关系.
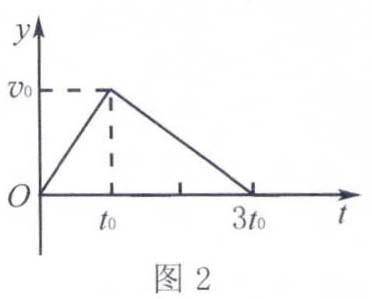
例1 一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速运动,接着做匀减速运动,开到乙地刚好停止,其v-t图象如图2所示,那么
0~t0 和t0~3t0,两段时间内
A.加速度大小之比为3∶1
B.位移大小之比为1∶2
C.平均速度大小之比2∶1
D.平均速度大小之比为1∶1
图象转换优势分析:图象转换可以直观地表现运动状态的变化,反映a、v、x三个物理量之间的关系.例如本题中条件量是速度v,则加速度a为v-t图象的斜率,得到0~t0和t0~3t0,两短时间内斜率分别是
v0t0和
-v02t0
.因此我们可以根据v-t图象画出a-t图象,如图3,这实际上是v-t图象的微分过程.而v-t图象与坐标轴围成的面积表示该汽车相应时间的位移x,与它的正是一种积分关系,如图4.x-t图象的描绘对思维能力的要求较高,教师如果此时稍加引导,抓住积分关系得到x-t图象,能帮助学生建立匀变速运动整体模型,是建立运动全局观的良性训练.
3 变力做功问题的图象转换
在功能关系的知识板块中,学生经常遇到的变力做功问题.当变力与物体位移线性相关时(例如空气阻力),我们可以利用F-x图象来得到该力做功的大小,因为F-x图象在该段位移里对物体所做的功在数值上正好等于F-x图象所围成的面积.同时,利用图象转换的方法,我们也可以得到该物体运动状态的相关的a-t图象、v-t图象,这对于学生分析变力作用下物体的运动状态有很大的帮助.
例2 一颗m=0.1kg的静止的小球从高达10m的楼层下落,下落过程中有空气阻力f阻,且f阻=kx,其中k=0.2N/m,x为下落的位移,求下落至地面时小球的速度为多少?(取g=10m/s2)
图象转换优势分析:结合函数图象以及图象之间的转换,可以避免复杂的代数计算,定性的帮助学生分析物理过程.例如本题,对于根据f阻=kx可以得到空气阻力的f阻-x图象,如图5.那么在下落过程中对该物体进行受力分析,利用牛顿定律得mg-kx=ma,由此可知,小球的加速度不断减小,直到重力与空气阻力相同时加速度减小为零,因此我们就可以得到a-t 图象(图6).此时,学生得到的结论是:当mg=kx0时,小球加速度为零,匀速运动,所以利用a-t图象,运动对象的物理情境清晰展现在学生脑海中.令此时的时刻为t0,可得此时位移x0=5m<10m,所以小球在着陆之前就已经匀速运动了.根据f-x图象在该段位移x0里对物体所做的功在数值上等于f-x图象所围成的面积,可以得到空气阻力做的功Wf=12kx2 ,再利用动能定理,得mgx0-12kx20=12mv2-12mv20就可以得到匀速时的速度大小.而与此同时,利用微积分思想的图象转换思路也可以得到v-t图象(图7),将该物体运动的状态用图象定性描绘出来,由图能得到的新结论是:该物体做的是变加速运动,它在空中匀速运动时的速度就是物体着陆时的速度.那么此时教师可以引导学生思考,假如该物体下落的高度小于5m,物体下落时加速度和速度是如何变化的?根据a-t、v-t图象答案就呼之欲出了.这个过程是在引导学生提出问题,发现问题,加深了学生对于此类物理过程本质的理解.
4 电、磁场问题的图象转换
带电粒子在变化的电、磁场中运动的问题涉及到力学和电、磁场知识的综合运用.在电场中,电场力的改变使得对象受力发生周期性改变,从而运动状态也随之改变,因此,我们可以从U-t图象通过图象推导得到v-t图象,进而利用积分关系分析获得x-t图象;在磁场问题中,根据法拉第电磁感应定律,磁场的变化也会导致感应电动势的改变而改变,由此我们也可以定性描绘出电势或电流的变化图象.
例3 如图8,匀强磁场的磁感应强度方向垂直于纸面向里,磁感应强度B随时间变化图象如图9所示,现有一个电阻为R,边长为l的方框位于磁场中,尝试画出其感应电流的变化图象.
图象转换优势分析:教师利用图象转换策略可以拓宽习题讲解的思路,例如本题的条件量是磁感应强度B,目标量是感应电流I.根据法拉第电磁感应定律E=
nΔΦΔt=nSΔBΔt,EμΔBΔt,则IμΔBΔt.即I=ER=l2kR,k为 磁场变化图象斜率.根据B-t图象的斜率,不需要右手螺旋定则的判定,我们可以很快得到I-t图象,提高了解题效率,如图10所示.
例4 将如图11所示的交变电压加在平行板电容器A、B两极板上,交变电压如图12所示,开始B板电势比A板电势高,这时有一个原来静止的电子正处在两板的中间P处,它在电场力作用下开始运动,设A、B两极板间的距离足够大,下列说法正确的是
A.电子一直向着A板运动
B. 电子一直向着B板运动
C.电子先向A板运动,然后返回向B板运动,之后在A、B两板间做周期性往复运动
D.电子先向B板运动,然后返回向A板运动,之后在A、B两板间做周期性往复运动
图象转换优势分析:如本题,根据公式a=
Fm=Uedm
,不难确定电子所受电场力的变化,从而获得加速度a变化图象,如图13所示,进而得到速度v变化图象,如图14.从图中可知,电子在第一个T/4周期时向B板做匀加速运动,T/4到T/2时匀减速运动,T/2到3T/4时反向加速运动,3T/4到T时匀减速运动.所以电子是在极板之间周期往复运动.因此,学生在利用图象再现物理情景的同时,利用图象转换思路可以拓宽解决问题的思维,由原问题得到新推论.
例4变式 此时如果利用微积分思想思考粒子运动位移的问题,就可以通过v-t图象定性描绘出x-t图象,电子在第一个T/4周期时向B板运动斜率为正不断增大,T/4到T/2时斜率为正不断减小,T/2到3T/4时斜率为负不断增大,3T/4到T时斜率为负不断减小,如图15所示.因此,我们得到的新结论就是:粒子从中点出发后是在P点的右半侧运动,不会运动到P点的左半侧.
5 波动问题的图象转换
在简谐振动问题中,我们经常会遇到振动图象和波动图象.波动图象(y-x图象)是所有质点某时刻时在空间内的分布图象;而振动图象(y-t图象)是描述某一质点的位移随时间变化而变化的图象.在研究简谐振动问题时,我们要将两个图象相互结合对质点振动进行分析.通过已知的条件量的图象,将y-x图象与y-t图象的相互转换,可以顺利解决简谐振动的图象问题.
例5 介质中坐标原点O处的波源在t=0时刻开始振动,产生的简谐波沿x轴正向传播,t0时刻传到L处,波形如图16所示.y-t图中能叙述x0处质点振动图象是
图象转换思路:题中所给条件图为t=t0时刻的波动图象,t0时刻波传到了L=3λ处,所以波动是从左向右传播的,且起振方向是向下的.而对于x处的质点来说,在t0时刻之后运动趋势应与x0左边的质点一致,即向下运动.所以在振动图象中t0右侧时刻质点的位置应该低于t0时刻质点的位置,因此只有C选项是正解.本题的难点在于如何从y-x图象转换到y-t图象,所以,抓住宏观的波动传播方向,再聚焦到某个质点的振动趋势上,是此类问题图象转换的关键.
例5变式 一列简谐横波沿直线传播,该直线上平衡位置相距9 m的a、b两质点的振动图象如图17所示,下列描述该波的图象可能正确的是
图象转换思路:该题考查的是学生将y-t图象转换为y-x图象,刚接触此题时,学生很难把握,不知道a、b点是哪个离波源更近,因此先假设简谐波由a向b传播,从振动图象看,b与a相差34+n个周期,所以a、b距离为c=(34+m)λ=9 m(n=0,1,2……).若假设波由b向a传播,a与b相差14+n个周期,所以a、b距离c=(14+n)λ=9 m(n=0,1,2……).本题解决的关键是要在两种假设下分别明确a、b的相位差,并且要认识到简谐振动的周期性.
由以上的实例可以看出,图象转换策略是教师和学生需要重视的一种思维模式,在高中学习中涉及面较广,对学生知识能力的考查也很深入.这一策略不仅能够帮助学生简洁快速地解决问题,并且对于学生完善物理知识体系,深化物理思想,提升思维能力都有重要的意义.

