高中生数学思辨习惯养成
南京一中实验学校(210000)
李红果 ●
高中生数学思辨习惯养成
南京一中实验学校(210000)
李红果 ●
思辨对概念教学的作用不可忽视,区别于计算数学的逻辑思维,通过思辨可理解概念,发现问题解法.在数学教学中有计划地安排学生思辨,对学生的习惯养成起到推动作用.
高中数学;思辨;习惯养成
荷兰数学家、数学教育家弗赖登塔尔((H.Freudenthal)提出思辨数学的概念,区别于计算数学,也称思辨数学为概念数学,就是动态地辩证地把握概念和体味推据,凭借对概念的直觉和数学美的启迪,而产生直观的解题思路方法或做出合情推理决策.也就是,在直觉的引领下,围绕推据,换位思考,在运动中找到解题方法的数学知识体系.目前的数学教学,重视计算数学中的逻辑推理,而轻视思辨数学中的直觉思维.思辨数学的作用往往会让学生的数学思想得到释放和创新,从而能从直观上判读解题思路的可行性,对学生的解题起到决定性的作用,所以数学教师有必要在课堂教学中引领学生思辨习惯的养成.
一、计划引领,照顾个体
学生的思辨习惯的养成不是一蹴而就,而要有计划实施,根据课程标准和教材要求编制整体计划,然后考虑单元计划、学时计划等.计划编制的原则是:一是新课程标准中的思维训练要求,思辨思维依托于计算思维,重在形成直观,要与其他思维相辅相成,不可盲目割裂.二是要研究教材中的概念、定理、公式等,对其成因、形成条件、适用范围、正反推据等都可以通过思辨,搞清概念,定理、公式等才能真正掌握他们,熟于心、达其意,在解题中方能辨别一个个基本问题.三是不能脱离学生实际,学生多会计算思维,高中学生更倾向逻辑思维,基于这两者的辩证关系,教师引导学生逐步辨析问题的数学模式,灵活使用思辨.四是要小梯度推进,在概念教学中可设置多个小问题,人人皆可参与,人人皆可有观点,分歧意见可讨论,理越辩越明,从而做到清晰概念的效果.
二、分步实施,激励引导
通过思辨,能让学生在解题中通过直觉发现解法或数学模型,这是我们的期望.学生数学成绩提不高的主要原因是找不到合适的解法,有解法的题通过计算和逻辑推理,自然能够做好,但没解法却是真正让学生头疼的事.概念教学来不得马虎,每一个因素都要辨析和追溯求源,有任何含糊不清的地方都会带来致命的错误.训练思辨要按计划分步实施,在小组讨论中充分发挥主观能动性,设置问题开始可有老师提出,以后可有小组提出,甚至可以互相提问,互相答疑.学生需要表扬等激励,教师要适时给予鼓励,关注他们的成长,夯实基础、形成技能,逐步培养与计算思维相当的思辨习惯.
对学生在思维方面的激励远比表扬其做好一个题目的效果好的多,对激发学生的学习兴趣作用很显著.激励办法可从以下几方面来做.一是融入小组的激励机制,纳为日常考核指标,对小组与小组间的竞争有一定的推动作用;二是思辨中表现较的同学可以引导其对竞赛数学的研究,以表明老师的重视态度,激发其学习数学的动力.三是关注每个学生的表现,找到其思维的亮点,适时表扬,事半功倍.
三、解题训练、效果为本
直观往往与图形相关联,尤其是学习函数性质、立体几何、三角函数、解析几何等内容时.比如指数函数教学
教师给出函数:y=2x、y=1.073x.
师:用字母a表示底数,则上面的式子可表示成y=ax的形式.这就是指数函数.下面请同学们研究讨论一下如何给指数函数下个定义.
点评 学生上课是有教材的,教材中对指数函数定义很明白的给出,学生根本就不用思考,只要看一下书就可说出函数概念.学生对底数的认识就不那么清晰了.
建议教师:边问边引导学生思辨.
1.对不同的a,对应函数式的值的问题,可分为如下问题思考:①若a<0,能否计算,对应函数是否存在?②若a≠0,函数是否存在?③若a=1,函数将如何?
2.指数函数与幂函数之间是否存在相似之处?是否有关联?

教师:你对这个定理如何理解?
点评 学生不知道从哪入手思考.得到的结论自然有很多偏离问题主题.建议教师:把这个问题设计为多个,然后分组讨论研究.(1)各边与其对角的正弦对应比例,还可以表示成什么形式? (2)如果把定理看成方程,那么这个等式可以看成几个方程?每个方程中应该已知几个量求几个量?
动手实验能增强感官刺激,加深对概念、图形的形成起到一定的作用.比如平面的基本性质的教学:
实验:把铅笔当作直线、白纸当做一个平面.(1)若铅笔的两个端点在白纸内,则铅笔所在直线上各点与白纸所在的平面有什么关系?(2)若铅笔有一个端点不在白纸所在的平面内,铅笔表示的直线与白纸表示的平面有什么关系?
引导学生得出:
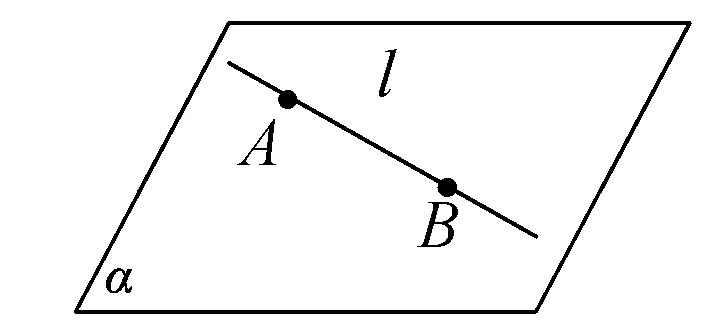
公理1 如果一条直线上的两个点在一个平面内,那么这条直线上所有的点都在这个平面内.
点评 作为公理,建议教师先介绍公理,让后可以做实验验证和理解,学生可以得出很多结论,但公理是共同约定的数学理论是建构空间立体几何的基点.
思辨的培养在图形中运用最普遍也最直接,通过点、线的移动或变化,可以有不同的结果,运用数学知识也不尽相同,既起到了训练的效果,也起到了对相关问题的理解,从而吃透问题的本质,建构所要研究的对象的蕴含关系.
四、变式训练,迁移创新
对问题的理解、方法的掌握可以通过对条件和结论的思辨做到更深的挖掘.常见的一题多解也是对学生的直观思维的考查,不同的学生对问题的理解程度不同会对问题的解决方法有不同的直觉,往往会产生不同的解法.同样地,同一个问题我们可以对条件进行放大或限制、结论的延伸和迁移,可以做到对学生的思辨训练.从近些年的高考来看,迁移创新问题也占有相当高的比例,新概念、新运算、新规则的问题也很多,解决此类问题主要靠课内的基础知识、基本技能、定理、原理等的理解,联想类比靠的是直观和平时的思辨积累.
思辨习惯的养成来自有计划的培养,不脱离计算思维,有疑有问,有思有辩,是夯实双基的必要条件.抓住问题的关键,对其产生与概念相关的直觉,通过逆向思维和发散思维,借助类比联想或换位思考,查找问题的各种关联,建立数学模型,进而运用逻辑推理解决问题.
G632
B
1008-0333(2016)30-0035-01

