高中立体几何中割补法教学研究

江苏省镇江市丹阳六中(212300)

郦荣霞●



高中立体几何中割补法教学研究

江苏省镇江市丹阳六中(212300)

郦荣霞●

新课改以来，高中的数学无论是在结构还是在内容上都改变了很多.其中，作为高中数学重点教学内容之一的立体几何也是改变了很多，立体几何在高中数学的教学当中既是重点也是难点.不同学生之间的空间想象能力存在很大的差异，部分学生甚至看不懂图形，难以理解题目的意思.因此，教师在教学中怎样教好学生学习立体几何是一个讨论的要点.

高中;立体几何;割补法

一、补形法

补形法是高中几何解题中最常见的一种方法，即补充原有的图形，形成新的图形模式，在新的图形中进行问题的解答，从而找到简单的补充方法得到结论.

1.构建成正方体或者是长方体

例2 如图，已知三棱台ABC-A′B′C′的侧面A′ACC′垂直底面ABC，且是梯形,梯形两底角互余，且∠ACB=90°，求证：另两个侧面互相垂直.

证明 延长三条侧棱交于点P.因侧面A′ACC′的底角互余，故∠APC=90°.即PA⊥PC.又面A′ACC′垂直于底面ABC,且BC⊥AC，故BC⊥面PAC.又PA⊂面PAC，故BC⊥PA.PA⊥面PBC.而PA⊂面PAB，所以面PAB⊥面PBC,即面A′ABB′与面B′BCC′垂直.

2.构建成其他的规则几何体

例3 如左图，一圆柱被一平面所截最长侧面母线为4，最短为1，圆柱底面半径为2，计算几何体的体积.

分析 如右图，再用相同的几何体，两个拼成一个圆柱，高为5.则几何体的体积应该就是圆柱体积的一半，即V=1/2×π×22×5=10π.

二、切割法

在高中的立体几何中，切割法属于比较特殊的一种求解方法，通过切割成几个部分的形式进行分析，简化问题，得出结果.

例4如图，已知正四面体的棱长为a，P是正四面体内部一点，求点P到各个面的距离之和.

分析 因为P是可以移动的任何一个点，因此到各个面的距离是无法计算的.为简化，假设P是顶点，到各个面积的距离可以认为是求解三棱锥的高，通过计算三棱锥的高得出结果.

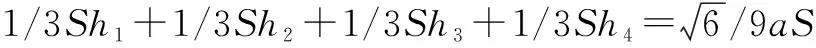
例5 已知多面体ABC-DEFG中，AB、AC、AD两 两 互 相 垂 直，平 面ABC∥平 面DEFG，平面BEF∥平面ADGC，AB=AD=DE=2，AC=EF=1，则该多面体的体积为( ).

A．2 B．4 C．6 D．8

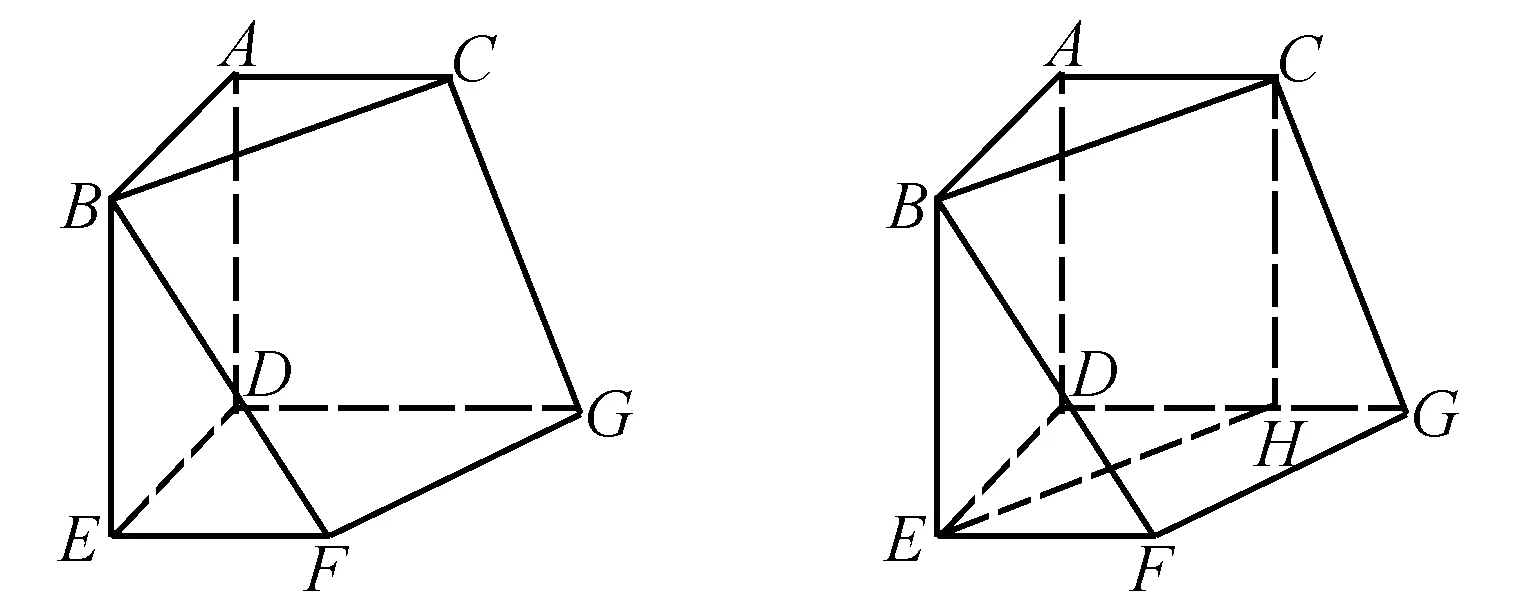
分析 如图，过点C作CH⊥DG于H，连结EH，这样就把多面体分割成一个直三棱柱DEH-ABC和一个斜三棱柱BEF-CHG.

V=S△DEH×AD+S△BEF×DE

=(1/2×2×1)×2+(1/2×2×1)×2=4.

本文主要是围绕割补法对学生在学习立体几何时容易遇到的问题进行分析和研究，希望这些问题能够在教与解立体几何时给教师和学生一些帮助.

[1]郭敏.苏教版高中必修教材中数学思想方法教学研究[D].南京师范大学,2014.

G632

B

1008-0333(2016)30-0037-01