基于Radon变换的超声穿刺针增强系统

符吉林闫桂霞凌锋

1 广东省医疗器械质量监督检验所 （广州 510663）

2 深圳市理邦精密仪器股份有限公司 （深圳 518067）

基于Radon变换的超声穿刺针增强系统

符吉林1闫桂霞2凌锋2

1 广东省医疗器械质量监督检验所 （广州 510663）

2 深圳市理邦精密仪器股份有限公司 （深圳 518067）

超声穿刺针增强算法一般基于超声发射的波束偏转技术，预先选择波束偏转角度，并利用图像融合技术增强针体。这种图像后处理方式容易受到噪声干扰，导致图像质量问题。本文算法在波束偏转的基础上，采用图像分割的方式进行图像后处理，首先使用radon变换和直线重建获得针体区域，该区域与正常B模式图像复合得到最终的显示图像，并经过一定的校正手段使结果更加稳定。算法简单有效，避免了噪声干扰。

穿刺针增强 多帧偏转 radon变换 radon校正

1.超声穿刺针增强系统简介

超声成像的基础是声波反射，反射能量经过一系列后处理形成图像。在穿刺过程中，穿刺针或者注射针要以一定的角度刺入患者体内，正常发射的声波不能以垂直角度接触针面，在反射中损失了针信号能量，针信号会变得非常不稳定甚至消失[1]。在2D超声成像中，通常由波束偏转和帧复合来解决增强问题[2]。在正常的垂直发射之外，添加合适的偏转波束，其声波发射角度要与针面大致垂直，从而得到的偏转帧图像上针的信号较为强烈。采用一定的方式将针信号提取出来，添加到正常组织图像中，使针信号变得清晰，帮助医生查看针头运动的位置。现有的超声产品一般需要预先设置波束偏转角度。开启穿刺增强之前，要由一定的外在参与改变发射偏转角[3]。

在获得偏转帧之后，一类算法是直接将偏转帧经过处理后与正常帧融合。这种算法处理后的针体区域比较稳定，但是增强效果较弱或者容易引入噪声。另外一类算法是把针体区域近似看做直线形态，单独分离出来，涉及到直线的分割和重建。霍夫变换是一种常见的直线分割方法，将直线的空间位置信息转化到角度-距离空间，可以很好地探测直线的位置和方向，但是难以控制直线的起始点，尤其是针体信号不稳定的情况下，针体在视频流中有长短变化，不能反映实时运动。Charles R.Hatt等[4]使用一种机器学习的方式来进行穿刺针的分割和增强。机器学习方式使用在实时图像中，有一定的局限性。

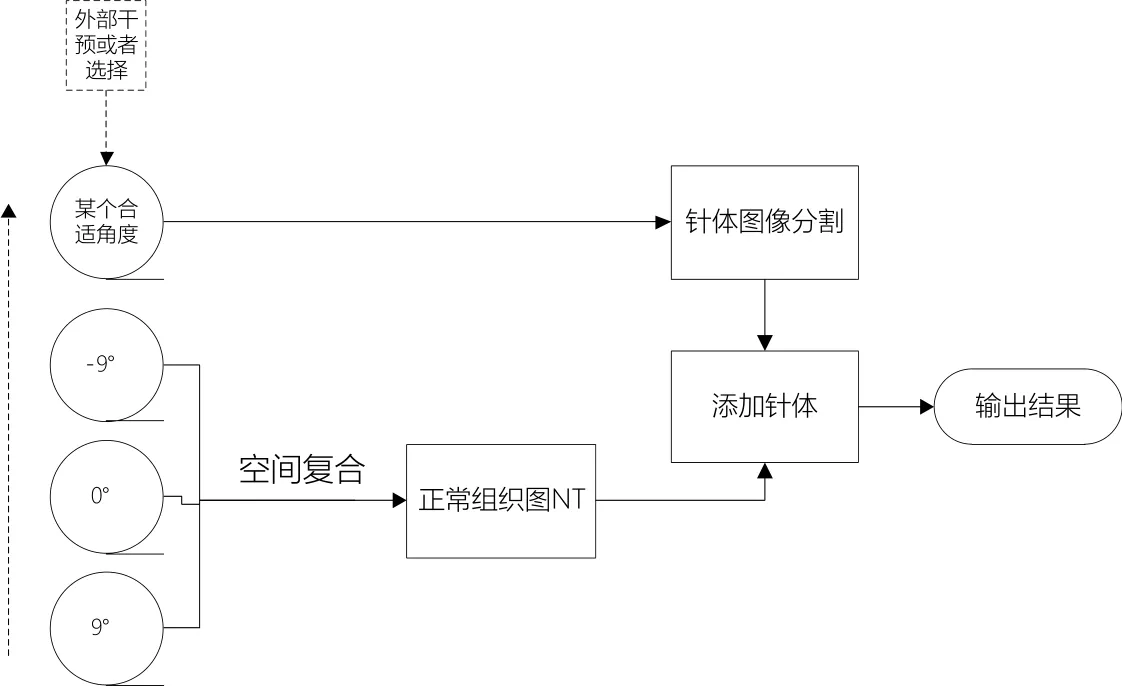
图1. 整体算法流程

本文针对上述现有技术的不足，提出一种基于radon变换的超声穿刺针增强系统。首先增加偏转帧发射，穿刺针在某个角度下会呈现高亮形态，出现在偏转图上。然后对偏转图进行两次OTSU分割，去掉绝大部分干扰，进行radon变换和radon校正。最后重建针体区域。并以一定权重与组织帧融合，达到增强目的。最终结果图像中，针体表现清晰稳定，去除了组织变形和器官边缘的干扰。整体算法流程如图1所示。

2.声波发射方式与图像获取

2.1 正常组织帧的获取

为了提高图像质量，以三帧方式获取正常组织图像，如图2所示分别以-9°，0°，9°发射声波，获取三帧图像。三图通过空间复合算法进行合成，输出一帧作为正常组织图像，设为NT。获取方式如图2所示。

2.2 偏转帧的声波发射

图2. 正常帧获取方式.垂直发射和对称偏转发射融合。用于穿刺针增强的7帧偏转发射方式与之类似。

外部设置人机交互界面，或者添加穿刺架。操作者根据实际需求，选择合适角度，由外部交互传入处理程序。

2.3 偏转图像的获取

针刺入后，偏转帧SF拥有最亮的针体部分，方便接下来的图像后处理。

获取NT和SF需要4个角度的图像，因此探头的声波发射以4个偏转角度为循环周期。为了不影响图像的帧率，采用轮流替换的方式，即建立4帧数据阵列，每接收一帧数据，替换阵列中相同角度的图像数据，然后进行接下来的后处理流程。

3.穿刺针区域分割与增强

3.1 Radon变换的原理

Radon变换可以将空间线检测转化到角度-距离空间，能在噪声图像中保持稳定。在角度-距离空间中，图像中的一条亮线表现为一个峰值，一条暗线表现为一个谷值，分别对应一个角度坐标和距离坐标。对于大小为MxN的图像来说，Radon在二维欧几里德空间的变换矩阵为：

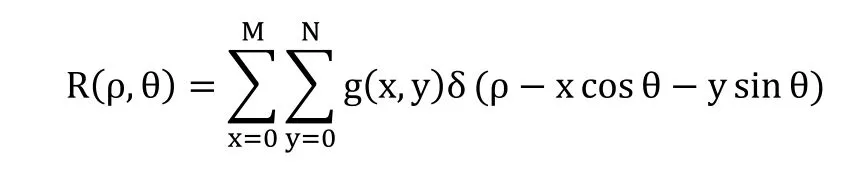
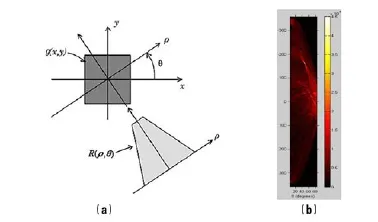
图3. Radon变换的几何意义和Radon矩阵

图4. 穿刺针区域分割算法流程

其中，δ（r）代表Dirac方程，二维空间中一条直线符合以下定义

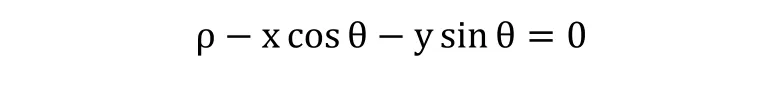
Radon变换几何意义如图3（a）所示。拥有一条长直线的图像的Radon矩阵如图3（b）所示。

Radon矩阵中横坐标代表直线偏角，纵坐标代表直线与中心的距离，每个点的亮度代表一条直线在图像中的积累量。亮度越大，代表直线积累越多，在二值图中表现为线上的点数越多。

因为穿刺针在图像中一般较长，较为连续，获得Radon矩阵后，搜索矩阵中最大值所在的位置（积累量最大，代表直线数据量大）的坐标ρ，θ，认为是穿刺针所在的直线的位置。这样的做法可以克服穿刺针图像可能出现的中断问题，增加检测稳定性。

3.2 基于Radon变换的直线分割

穿刺针区域分割算法流程如图4所示。

偏转图SF进行两次OTSU分割，去除多余干扰。OTSU是一种基于直方图的图像分割算法，能自动分析图像的分割阈值点，将图像分为两部分。一个离散概率密度函数的归一化方程如下所示：

其中，n是图像中的像素总数，nq是灰度级为rq的像素数目，L是图像中所有可能的灰度级数。假设我们现在已经选定了一个阈值k，C0是一组灰度级为[0,1,…, k-1]的像素，C1是一组灰度级为[k,k+1,…, L-1]的像素。OTSU方法选择最大化类间方差σ2B的阈值k。得到k值后，即可

第一次OTSU分割：将较暗的噪声和背景设置为0；

第二次OTSU分割：根据上一步的结果再进行一次OTSU，分割出高亮部分，得到二值图ImageBaniry。根据ImageBaniry分辨率建立二维欧几里得空间，重建一条直线，用以下直线方程表示：

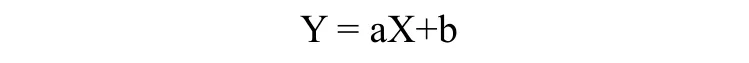
其中，a为直线斜率，b为直线与y轴交点坐标。a，b的具体数值由ρ，θ经过一定的转换后得来。

获取直线后，在SF中以直线为中心扩展出一个15像素宽度的条带区域，取出条带区域，设为BandLine。

为了避免直线搜索时可能出现的假线问题，将设置以下限制条件：

（1）根据具体图片情况，b值应大于0或者小于0；

（2）BandLine中像素二值化，然后找出其中的最大连通区域LineMaxR，其长度必须大于某个阈值；

（3）LineMaxR斜率与a的差值必须小于某个阈值。

3.3 Radon数值校正

针的图像区域通常会有一定的宽度，因此使用Radon变换最大值搜索直线所在位置的时候，会出现偏离中心线，搜索到对角线的情况。如图5（a）所示，为了显示方便，线段区域设置为黑色。这种情况会使重建后的针区域位置出现上下帧之间的微小偏差，表现为轻微的抖动，并且会偏离真实的针体位置。经过一定的校正措施后，直线位置如图5（b），可见校正措施起到了良好的效果。

校正措施过程如下：

对于一个有宽度的线段区域BandL，其Radon变换矩阵如图6（a）所示。BandL的上边缘和下边缘各有一条直线，可以认为BandL拥有两个ρ，两个θ。6（b）中示意了线段区域的ρ分布。如果直线仅需要ρ值的校正，那么：

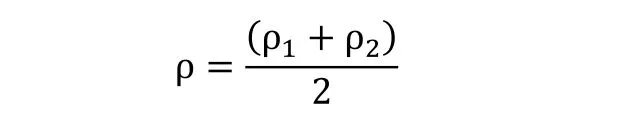
同理，如果直线仅需要θ值的校正，则有：

线段中通常会出现对角线方向的偏差，即ρ，θ同时需要校正。为了达到这个目的，可以对BandL的Radon变换矩阵使用一个均值滤波，在滤波后的结果中搜索最大值来确定直线中心线。均值滤波的模板大小要由线段宽度而定。本算法使用的模板大小为3X3。

图5. Radon校正前后的直线检测对比

图6. (a)有宽度的线段的Radon变换数值矩阵 (b)ρ值分布示例

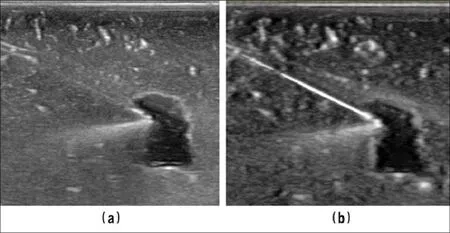
图7. 穿刺针增强前后对比，图像为模体穿刺结果。(a)增强前(b)增强后

3.4 穿刺针复合增强

经过以上环节获取最终直线后，在SF中以直线为中心扩展出一个15像素宽度的条带区域，并以此区域像素与正常组织图像NT进行融合，达到穿刺针增强的目的。增强前后效果如图7示意。

4.结论

本文提出了一种基于Radon变换的穿刺针增强算法，在波束偏转后获得的偏转帧上进行直线分割，较好的获得针体区域。增强后的针体部分清晰锐利，针尖完整，且噪声影响小，效果稳定。整个算法简单有效，开启算法后图像流畅自然，具有很强的实用性。

[1] Michael B. Stone , Cynthia Moon, Needle tip visualization during ultrasound-guided vascular access: short-axis vs longaxis approach, American Journal of Emergency Medicine (2010) 28, 343-347.

[2] Nikolaos Pagoulatos, Qinglin Ma, Andrew K. Lundberg, System and method for enhanced imaging of objects within image, United States Patent, US 2011/0249878 A1.

[3] Janjun Guo, Feng Lin, Menachem Halmann, Method and apparatus for enhancing needle visualization in ultrasound imaging , United States Patent, US 2012/0209107 A1.

[4] Charles R Hatt, Enhanced Needle Localization in Ultrasound Using Beam Steering and Learning-Based Segmentation, COMPUTERIZED MEDICAL IMAGING AND GRAPHICS · JULY 2014.

[5] Mert Kaya and Oz Automat kan Bebek, Needle Localization Using Gabor Filtering in 2D Ultrasound Images, IEEE International Conference on Robotics and ion (ICRA 2014)

Ultrasound Needle Enhancement System Based on Radon Transform

FU Ji-lin1YAN Gui-xia2LING Feng2
1 uangdong Medical Devices Quality Surveillance and Test Institute (Guangzhou 510663)
2 EDAN INSTRUMENTS,INC. (Shenzhen 518067)

Needle enhancement visualization algorithms are usually based on beam-steering, which needs users to set one beam steering angle at first, and also needs to enhance the needle by image blending. This kind of image post-processing may result in the image looking badly because of noise from steering frame. The method proposed in this paper use image segmentation as image post processing after beam-steering. Radon transform algorithm is applied to detect the needle location and orientation in the steering frame. After radon value correction, the needle region is compounded with the normal tissue frame to get the display frame. This method is simply but effective and it avoids noise.

needle enhancement, beam steering, radon transform, radon correction

1006-6586(2016)07-0058-05

R445.1

A

2015-10-08