干发酵库充气密封圈非线性有限元分析
李瑞容, 朱德文, 王鹏军, 韩柏和, 陈明江, 陈永生
(1.农业部南京农业机械化研究所, 南京 210014; 2. 农业部农村可再生能源开发利用重点实验室, 成都 610041)
干发酵库充气密封圈非线性有限元分析
李瑞容1,2, 朱德文1, 王鹏军1, 韩柏和1, 陈明江1, 陈永生1
(1.农业部南京农业机械化研究所, 南京 210014; 2. 农业部农村可再生能源开发利用重点实验室, 成都 610041)
文章基于非线性有限元理论,考虑密封结构的材料特性、几何形状和接触的非线性,建立了“M”形充气密封圈的平面应变有限元模型,分析了充气密封机理,得到了法向接触应力沿密封接触面的分布规律,讨论了充气压力、被密封介质压力和密封间隙对法向接触应力和密封效果的影响。结果表明,保证密封效果的法向接触应力随充气压力的增大而增大,接触横截面宽度也随之增长,在外表面中间的凹陷圆弧部分达到应力峰值;被密封介质压力使得靠近介质一侧的接触应力减小,密封面长度变短;随着密封间隙的增加,其接触应力也相应增大。为了提升充气圈的密封性能,需要结合密封圈的受力变形、环境温度、压力和材料特性等综合进行结构设计,密封圈的表面应做涂层防腐处理;选择适当的被密封介质压力和充气压力比值,既能保证密封效果又能延长充气圈的使用寿命。
充气式密封; 非线性有限元; “M”形充气圈; 硅橡胶
干法发酵具有产生沼液少、容积产气率高、物料适应范围广和运行稳定的优点,无湿法发酵中的浮渣、沼液难处理等问题,受到了越来越多的关注。规模化沼气干法发酵装置主要有车库型、气袋型、渗出液存储桶型、干湿联合型和覆膜槽型等,其中车库型干法发酵装置容易实现扩展和规模化应用,具有运行管理简单、能耗低、利用效率高、通用性强等优点,应用前景广阔[1-3]。
为了满足装载机的快速进出料,发酵库门一般开在发酵库的侧面,大门的密封面积大;密封面易有杂物,产生间隙;发酵物料成分复杂,腐蚀性强等问题导致密封难的现象。国内外已有学者开展了相关密封系统的研究,韩捷[4]等采用气涨式夹紧密封方式对敞口式覆膜槽生物反应装置进行密封,进出料方便,气体易排尽,但密封面积大,密封效果难保障,且设计的深度和容量受密封面积大小所限;赵国明[5]等在地面车库型发酵槽敞口处采用辅助加强膜式封口、双闭合液涨式密封结构,反映直观,安全可靠,但该方法仅适用于全年零度以上的地区,且密封面积过大,存在安全隐患;黑龙江省宾县引进德国的密封技术,采用液压驱动和粘黏式矩形充气圈组合的密封方式,便于进出料,自动化程度高,但成本高,充气圈底部易脱落,密封缺少可靠性和稳定性;陈永生、朱德文等研究开发的柔性顶膜车库式干发酵装置采用复合“M”形气涨式机械压紧密封技术,双重密封安全可靠,可调节密封间隙,但需要空压机供气保证圈内气压。可见,针对复杂的沼气运行工况,复合“M”形气涨式机械压紧密封技术是比较合适的密封方式之一。
目前,非线性有限元法被广泛的应用于橡胶类密封圈数值模拟研究,但仅有少数针对充气式密封结构,孟祥铠[6]等利用MARC对“a”形充气密封结构进行了分析,贲可存[7]等利用ANSYS对“V”形充气式柔性密封圈进行了分析,周仕明[8]等利用MARC对充气式自密封气囊进行了分析,但对于“M”形充气密封结构未见报道。本文利用大型有限元分析软件ABAQUS,建立了截面结构为“M”形充气密封圈的轴对称有限元模型。分析了充气圈的变形情况,以及充气压力、被密封介质压力、密封间隙对法向接触应力的影响,为充气密封圈的结构设计和优化提供理论基础。

1.密封圈垫片; 2.充气密封圈I; 3.紧固圈部件; 4.螺栓; 5.平垫圈; 6.螺母; 7.充气密封圈II; 8.密封圈卡箍; 9.大门门体图1 复合“M”形充气密封圈固定安装方式示意图
1 “M”形充气密封圈结构和工作原理
发酵库大门采用复合“M”形充气圈组合密封技术,采用夹具固定的方式安装在大门的四周,主要由两个“M”形充气密封圈、垫片、紧固圈、卡箍等组成,如图1所示,两道密封圈中间用紧固圈压紧螺栓固定,两侧分别用垫片和卡箍加夹紧,使得密封圈既可以固定住也可以有一定的伸缩余量。
该充气密封圈材料选用以硅橡胶为基体材料,白炭黑为增强纤维,并添加硅油和硫化剂等。形状设计为“M”形,实际尺寸25 mm(宽度)×20 mm(高度),壁厚3 mm。大门关闭后,利用空压机对充气圈加压,充气密封圈凹陷部位向外膨胀变形,与刚体门框相挤压达到密封效果;当发酵完毕后,将充气圈内的压力卸载,密封圈脱离门框恢复充气前“M”形。考虑到充气密封圈因为长期工作磨损、气压不稳定等因素撕裂或泄漏,设计了两道并行充气密封圈,一旦其中一个密封圈发生破裂,另一个密封圈将保证发酵库气密性和稳定性。影响充气圈密封性能的因素主要有充气密封圈的接触应力、结构形式、材料回弹性能、充气压力、被密封介质压力、密封间隙大小以及接触表面粗糙度[9]等。
2 “M”形充气密封圈有限元模型
2.1 基本假设
(1)由于大门的门体、门框和固定件的刚度较大,不考虑其变形,将门框、固定件和接触的门体视为刚体边界;
(2)充气密封圈采用的是硅橡胶材料,视为不可压缩的而且在变形前是各向同性的;
(3)充气密封圈沿着门框安装在大门四周,周长远大于密封圈的高度和宽度,因此,密封圈及其接触边界均按平面应变问题处理。
2.2 材料定义
确定弹性体材料的非线性特性是困难的,但基于应变能密度用于大弹性变形的几种本构理论已经发展起来,对于橡胶类物理非线性材料,常用Mooney-Rivlin模型来描述[10]:
W=C10(I1-3)+C01(I2-3)
式中,C10和C01为Rivlin系数,均为正定常数。对于大多数橡胶而言,在应变为150%以内时可得到合理的近似。
采用两参数的Mooney-Rivlin模型进行计算,待定的材料参数可通过理论估算的方法求得。该方法是建立在以下理论基础上:初始剪切模量G= 2(C10+C01)和弹性模量E≈ 3G。利用橡胶材料的邵氏硬度HA计算弹性模量[8,11]。
再利用经验公式(C10+C01)=E0/6,C01=0.25C10,即可得到两参数的Mooney-Rivlin模型的材料参数值。
2.3 有限元模型
充气密封圈材料为硅橡胶,硬度HA为55,采用Mooney-Rivlin模型,参数由上诉公式计算得出。根据气囊的实际结构,考虑材料的不可压缩性,对硅橡胶采用四节点四边形完全积分不可压缩Herrmann轴对称单元,对大变形大应变的部位重划网格保证单元的质量和计算的精度。模型中考虑密封圈底部与发酵库门、密封圈顶部与门框的接触,接触间的摩擦采用库仑摩擦模型,摩擦因数f=0.1,将充气密封圈定义为变形体,采用离散描述;大门门体、固定件和门框定义为刚体,采用解析描述,并建立接触体间的接触关系。
根据实际工程运行情况,对该模型先施加内压,待充气密封圈膨胀稳定后,再施加被密封介质压力。由于被密封介质压力对充气密封圈外表面作用范围不可预知,采用预先加载充气圈内压力,待膨胀稳定后将实际接触面的路径用ABAQUS标记,再重新加载充气圈内压力和被密封介质压力。该模型采用大位移全Lagrange格式的增量方法处理充气密封圈的大变形几何非线性问题,通过调整加载时间步长即可得到稳定的计算结果。
3 “M”形充气圈密封性能分析
3.1 等效应力与变形分析
图2~图4显示了充气密封圈原始状态的网格划分情况,不同加载阶段的整体变形和von-Mises应力分布情况。从图2中可以看出,充气密封圈未充气时,呈现原始的“M”形,与顶部的大门门框存在一个密封间隙;如图3所示,当充气密封圈内充入一定压力的气体后,顶部的“M”形向外膨胀变形逐渐与顶部的大门门框贴合挤压,将间隙填满;如图4所示,在充气密封圈右侧加载了被密封介质压力Po后,密封圈右侧部分受到挤压脱离了与门框的接触,接触横截面宽度变小。充气压力加载后,接触面处充气密封圈的应力分布呈轴对称分布,其中凹陷圆弧部位的应力达到峰值,充气密封圈的最大等效应力主要出现在“M”形左右两侧内部圆弧面、顶部凹陷圆弧与门框接触面处。这主要由于这几处圆弧部位发生了较大的弯曲变形,弯曲应力较大。因此,进行“M”形几处圆弧角度的设计中,需选择合适的倒角半径,既保证有足够的接触应力,又不至于圈内应力长期过大使得工作寿命降低。

图2 充气密封圈原始状态
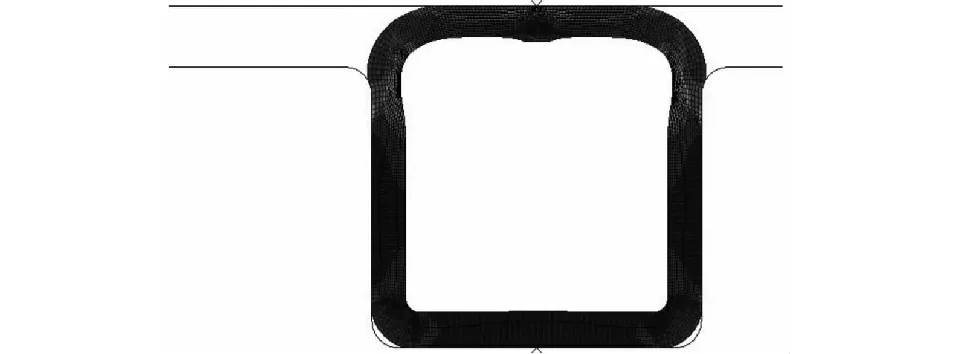
图3 充气密封圈充气状态

图4 充气密封圈密封状态
3.2 充气压力对接触应力的影响
当密封间隙D=5 mm,被密封介质压力Po=0 MPa时,对“M”形充气密封圈分别充入0.10 MPa,0.15 MPa和0.20 MPa的压力,如图5所示为不同充气压力下沿着密封面的接触应力分布曲线,可见法向接触应力随充气压力Pi的增大而增大。充气密封圈膨胀后密封接触横截面宽度约为14 mm,接触应力呈轴对称分布,整体呈现中间突出的倒“U”曲线形式。在接触面中间2 mm的长度范围内,接触应力随着密封圈的过度膨胀急剧增大达到峰值,这主要由于密封圈“M”形中间的凹陷圆弧部分,受到充气压力的强力反方向挤压,大幅度变形而造成。

图5 不同充气压力下接触应力沿密封面分布曲线图
为了确保充气圈的密封效果,在密封连接结构的接触面上,法向接触应力必须大于或等于被密封介质的压力。如图5所示充气圈内压力在0.10 MPa~0.20 MPa之间,接触应力值基本在0.50 MPa以上,最高达到2.24 MPa;正常工作时,被密封介质的压力在0~1000 Pa之间,接触应力远远大于被密封介质的压力,且接触应力峰值提高了充气圈的密封性能。随着充气压力的增大,法向接触应力不断增大,接触横截面宽度也随之增长,充气圈的密封性能不断增强。但同时也需考虑到充气圈的应力过大容易导致硅橡胶老化和密封失效,因此,要综合分析选择合适的充气压力。
3.3 被密封介质压力对接触应力的影响
图6 所示为充气压力Pi=0.20 MPa,密封间隙D=5 mm时,不同被密封介质压力下接触应力沿密封面分布曲线图。在“M”形充气密封圈内加载0.20 MPa的压力后,模拟工作状态,在充气圈的右侧分别加载0 MPa,0.05 MPa,0.10 MPa的被密封介质压力。从图6中可知,密封圈与被密封介质接触的一侧在被密封介质压力的作用下,法向接触应力不断减少,且波动较大;另一侧的接触应力略有增加;密封圈受到挤压脱离了与门框的接触,接触横截面宽度也随之变短。
当密封圈受到库内气体和沼液的压力作用时,密封面被迫发生分离,此时就要求密封圈能释放出足够的弹性应变能,能够弥补这个分离量,并留有保持密封所需要的接触应力[12]。因此,在提高密封圈的接触应力的基础之上,需选择适当的密封介质压力和充气压力比值,既能保证密封效果又能延长充气圈的使用寿命。同时,为了提升充气圈的吹出抗力,可以结合密封圈的受力变形、环境温度和材料特性等综合进行结构设计,例如加大充气圈和门框密封面的摩擦力,特别是接触密封介质的一侧,密封圈的表面还应做一些涂层防腐处理。

图6 不同被密封介质压力下接触应力沿密封面分布曲线图
3.4 密封间隙对接触应力的影响
图7所示为充气压力Pi=0.20 MPa,被密封介质压力Po=0 MPa时,不同密封间隙下接触应力沿密封面分布曲线图。随着密封间隙的增加,要求密封圈膨胀拉伸量也增加,导致其内部接触应力也相应增大。

图7 不同密封间隙下接触应力沿密封面分布曲线图
虽然密封间隙较大的时候,圈内的接触应力也较大,能带来较好的密封效果;但是,如果密封间隙过大,一方面会带来接触应力增加,大大降低了材料的使用寿命,对材料的性能要求较高;另一方面容易造成“M”形的展开程度不够,即中间圆弧角半径大的部位展不开,与密封面产生空洞,形成两段接触面,如图8所示,为密封效果带来隐患。因此,需要根据充气圈的结构、材料、尺寸和充气压力、密封介质压力,选择合适的密封间隙。
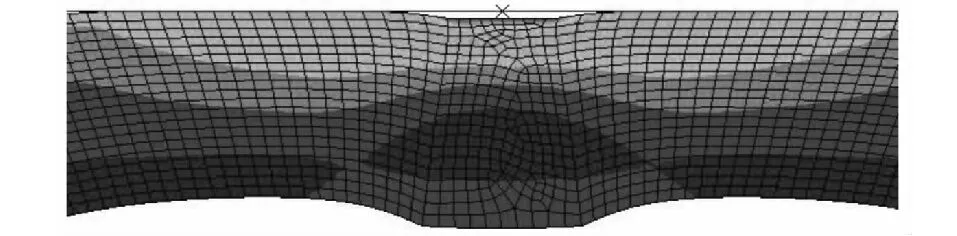
图8 密封面空洞图
4 结论
(1)通过有限元分析变形情况可知,“M”形充气密封圈最大von-Mises应力主要出现在“M”形左右两侧内部圆弧面、顶部凹陷圆弧与门框接触面处。因此,要选择合适的倒角半径,既保证有足够的接触应力,又不至于圈内应力长期过大使得工作寿命降低。
(2)法向接触应力是保证密封效果的关键,该应力随充气压力的增大而增大,接触横截面宽度也随之增长,在外表面中间的凹陷圆弧部分达到应力峰值;被密封介质压力使得靠近介质一侧的接触应力减小,接触横截面宽度变短;随着密封间隙的增加,其内部接触应力也相应增大。
(3)为了提升充气圈的密封性能,需要结合密封圈的受力变形、环境温度、环境压力和材料特性等综合进行结构设计,密封圈的表面还应做涂层防腐处理;选择适当的密封介质压力和充气压力比值,既能保证密封效果又能延长充气圈的使用寿命。
(4)利用有限软件ABAQUS对充气密封圈进行仿真模拟和优化设计是可行的。
[1] Kotter M. DRY Fermentation-A New Method For Biological Treatment[J/OL].http://www.gtz.de/ecosan/download/CESMA2002-Koettner.pdf,2007-10-20.
[2] Kottner M. Anaerobic systems for biological treatment in ecosan[EB/OL].http://www2.gtz.de/dokumente/oe44/ecosan/cb/en-anaerobic-system-ecosan-biogas-fertilizer-2005.pd,2007-10-20.
[3] Zhang Ruihong. Developing a R.D.T Digester System with Built-In Flexibility [EB/OL]. http://www.jgpress.com/Energy05/Zhang_M.pdf,2008-01-28.
[4] 韩 捷, 向 欣, 李 想. 覆膜槽沼气规模化干法发酵技术与装备研究[J]. 农业工程学报, 2008, 24(10):100-104.
[5] 赵国明. 规模化干法沼气发酵技术及装备的研究与示范[D].长春:吉林大学, 2009.
[6] 孟祥铠, 吴大转, 王乐勤. 充气密封的非线性有限元分析[J]. 润滑与密封, 2007, 32(3): 110~112.
[7] 贲可存, 汤文成, 徐鸿翔. 充气式柔性密封的非线性有限元分析[J]. 润滑与密封, 2008, 33(3): 69~71.
[8] 周仕明, 李道奎, 唐国金. 充气式自密封气囊结构的非线性有限元分析[J]. 润滑与密封, 2010, 35(10): 59~63.
[9] B N JPersson, O Albohr, C Creton, et al. Contact area between a viscoelastic solid and a hard randomly rough substrate[ J]. Journal of Chemical Physics, 2004, 120(18):8779 -8793.
[10] 王 伟, 邓 涛, 赵树高. 橡胶Mooney-Rivlin模型中材料常数的确定[J].特种橡胶制品,2004,25(4):8-10.
[11] Gent Alan N. Engineering with Rubber: how to Design Rubber Components[M]. Hanser Publishers, 2001.
[12] 付 平, 常德功. 密封设计手册[M]. 北京: 化学工业出版社, 2009: 157-170.
Nonlinear Finite Element Analysis of Inflatable Seals in the Garage-type Dry Fermentation Tank /
LI Rui-rong1,2, ZHU De-wen1, WANG Peng-jun1, HAN Bo-he1, CHEN Ming-jiang1, CHEN Yong-sheng1/
( 1.Nanjing Research Institute for Agricultural Mechanization, Ministry of Agriculture, Nanjing 210014, China; 2.Key Laboratory of Development and Application of Rural Renewable Energy, Ministry of Agriculture, Chengdu 610041,China)
Based on nonlinearity finite element theory of large deformation and contact problem, a 2D plane finite element model of M-shaped inflatable seal was derived. The seal mechanism was analyzed and the distribution rule of normal contact stress along sealing surface was obtained. The influence of loading pressure, sealed pressure and sealing gap on normal contact stress were discussed. Results showed that the normal contact stress was important to assure a safety sealing, which increased with the increase of loading pressure, reaching the peak in the middle of outside surface, and the length of sealing surface increased as well. With the action of the sealing pressure, the normal contact stress on the side of sealing media was cut down and the length of sealing surface got shortened. With the increase of sealing gap, the normal contact stress also increased. To promote the sealing performance, the structure of inflatable seal needs to be designed according to the stress deformation, environmental temperature, sealing pressure and material properties. It is needed to add a corrosion resistant coating on the surface of seals. And it is crucial to choose the suitable ratio of sealing pressure and loading pressure, which could ensure the sealing effect and prolonging the life of inflatable seals.
inflatable seals; nonlinear finite element; M-shaped seals; silicon rubber
2015-10-27
2016-01-19
项目来源: 农业部农村可再生能源开发利用重点实验室开放课题基金资助项目(2013009); 江苏省自然科学基金资助项目(BK20151073)
李瑞容,(1984-),女,汉,江苏南京人,助理研究员,主要从事农业废弃物处理与资源开发技术研究工作,E-mail:lrr006@163.com
陈永生,E-mail:cys003@sina.com
S216.4
A
1000-1166(2016)02-0066-04

