Modified filtered importance sampling for virtual spherical Gaussian lights

Yusuke Tokuyoshi()

Research Article

Modified filtered importance sampling for virtual spherical Gaussian lights

Yusuke Tokuyoshi1()

This paper proposes a modification of the filtered importance sampling method,and improves the quality of virtual spherical Gaussian light(VSGL)-based real-time glossy indirect illumination using this modification.The original filtered importance sampling method produces large overlaps of and gaps between filtering kernels for high-frequency probability density functions(PDFs). This is because the size of the filtering kernel is determined using the PDF at the sampled center of the kernel.To reduce those overlaps and gaps,this paper determines the kernel size using the integral of the PDF within the filtering kernel.Our key insight is that these integrals are approximately constant,if kernel centers are sampled using stratified sampling.Therefore,an appropriate kernel size can be obtained by solving this integral equation.Using the proposed kernel size for filtered importance samplingbased VSGL generation,undesirable artifacts are significantly reduced with a negligibly small overhead.

filtered importance sampling；real-time rendering；global illumination；virtual point lights

1 Introduction

The filtered importance sampling method[1]is a variance reduction technique of Monte Carlo integration often used for real-time or interactive rendering,which uses filtering kernels instead of sample points.This paper proposes a modification of filtered importance sampling,and improves the quality of virtual spherical Gaussian light(VSGL) [2]based real-time glossy indirect illumination using this modification.The original filtered importancesampling first samples the center of each filtering kernel according to a probability density function (PDF),and then determines the size of each filtering kernel using the PDF at the sampled center. However,this kernel size determination produces large overlaps of and gaps between filtering kernels for high-frequency PDFs(Fig.1).This is because the kernel size can be too large when the sampled center is at a local minimum of a high-frequency PDF. Therefore,this paper introduces an appropriate kernel size of filtered importance sampling to reduce these overlaps and gaps.

1 Square Enix Co.,Ltd.,Tokyo,160-8430,Japan.E-mail: tokuyosh@square-enix.com().

Manuscript received:2016-08-31；accepted:2016-09-21

Fig.1 Sampling VPL clusters from a reflective shadow map based on filtered importance sampling.Red points:kernel centers sampled according to the PDF(brightness).Orange squares:filtering kernels (i.e.,VPL clusters).The previous filtered importance sampling(a) produces significant overlaps of and gaps between filtering kernels. Our method(b)reduces these overlaps and gaps.

One effective application of our method is generation of VSGLs using reflective shadow maps [3].Reflective shadow map-based global illumination is well established for real-time rendering.However, stochastic sampling of virtual point lights(VPLs)[4] (i.e.,texels of reflective shadow maps which represent one-bounce light subpaths)produces noticeable variance especially for glossy interreflections.To reduce this variance,VSGLs were introduced

recently.A VSGL approximates a cluster of VPLs using a Gaussian-based representation.Thanks to this representation,the distribution of VPLs can be filtered with a simple summation operation(e.g., mipmaping). In addition,this representation has an analytical solution of the rendering integral for each VSGL.Therefore,if VSGLs are generated from reflective shadow maps inexpensively,we are able to render one-bounce glossy indirect illumination at real-time frame rates.

Tokuyoshi[2]sampled VPL clusters as VSGLs from a reflective shadow map based on filtered importance sampling to achieve real-time frame rates.However,while this approach is simpler and faster than k-means-based VPL clustering[5,6],it does induce flickering structured artifacts due to the previously mentioned overlaps and gaps.This problem is noticeable when a bidirectional reflective shadow mapping method[7]is used to build the PDF.This is because the bidirectional reflective shadow mapping method produces a dynamic and high-frequency PDF.Using our kernel size,we are able to reduce flickering artifacts significantly for such a high-frequency PDF.

The contributions of our work are as follows:

·An appropriate kernel size of filtered importance sampling is introduced to reduce undesirable overlaps of and gaps between filtering kernels.

·For image-based PDFs,the above kernel size is computed using a simple numerical approach with negligibly small overhead.

·Using the proposed filtered importance sampling method,flickering artifacts are reduced for VSGL-based real-time glossy indirect illumination.

2 Related work

2.1 Sampling with pre-integration

Sampling pre-integrated values is often used for image-based lighting.Structured importance sampling[8]stratifies samples hierarchically,and then the illumination is pre-integrated within each stratum.Debevec[9]subdivided an environment map into regions of equal energy using a median cut algorithm.This method approximates each region with a directional light source whose color is the sum of pixel values within the region.Filtered importance sampling[1]is introduced for glossy materials under environment maps. This technique samples prefiltered values using a mipmap,thus it performs at real-time frame rates.This paper modifies the kernel size of filtered importance sampling to improve the sampling quality.

2.2 Real-time global illumination

In this paper,we apply the proposed filtered importance sampling technique to real-time global illumination.Interactive global illumination algorithms were surveyed by Ritschel et al.[10].For a comprehensive survey of VPL-based rendering,we refer the readers to Dachsbacher et al.[11].Here we pay attention only to the most relevant works.

Virtual point lights(VPLs)are often used for representing indirect illumination[4].For realtime rendering,single-bounce VPLs lit from point or directional lights can be generated by using reflective shadow maps[3].Hundreds or thousands of VPLs are often resampled from a reflective shadow map by hierarchical sample warping[12] according to a mipmapped image-based PDF[13]. To generate shadow maps for so many lights,Ritschel et al.[14]proposed imperfect shadow maps.In their follow-up paper[7],a bidirectional reflective shadow mapping method was introduced to estimate a viewdependent importance for the image-based PDF. This method roughly computes the contribution of light paths from the eye to each reflective shadow map texel,and thus generates dynamic and highfrequency PDFs.Therefore,it can increase flickering artifacts,even though the total variance can be reduced.To take such dynamic PDFs into account, Barák et al.[15]introduced a temporally coherent sampling technique based on the Metropolis–Hastings algorithm for static light sources.They also proposed tessellation-based imperfect shadow maps to reduce memory usage.While the original VPL method is theoretically unbiased,variance is visible as spiky artifacts especially for glossy materials [16].To avoid this problem,VPLs are often clustered and then represented using a smaller number of area lights for interactive rendering.

Area light approximation via VPL clustering.Dong et al.[5]clustered VPLs using the k-means algorithm,and then approximated visibilities of VPLs using a soft shadow map for each cluster.Prutkin et al.[6]clustered texels of a reflective shadow map based on k-means similar to

Dong et al.,while they approximated the clusters with area lights for analytical radiance evaluation. They sampled cluster centers using the bidirectional reflective shadow mapping method to improve the quality.Luksch et al.[17]clustered VPLs using a kd-tree to generate virtual polygon lights to update light maps.These virtual area lights were evaluated using analytical form factors which cannot reduce variance caused by high-frequency bidirectional reflectance distribution functions(BRDFs).To allow for all-frequency BRDFs,recently spherical Gaussians have been used.

Spherical Gaussians[18,19]are often used for approximating the rendering of various types of materials under environment maps or area lights [20–24].This is because they have closed-form solutions for the integral,product,and product integral,which are fundamental operations to evaluate rendering integrals. Hence,all-frequency materials can be rendered efficiently.To represent static environment maps using spherical Gaussians, they have been fitted in preprocessing.For dynamic indirect illumination performed at near-interactive frame rates,Xu et al.[25]approximated the outgoing radiance using spherical Gaussians for each triangle primitive lit from distant light sources. Virtual spherical Gaussian lights(VSGLs)[2]were introduced to approximate a set of VPLs.To generate thousands of VSGLs at real-time frame rates,a filtered importance sampling-based approach was used with mipmapped reflective shadow maps. To generate a few VSGLs for more time-sensitive applications such as video games,the total value of all the reflective shadow map texels were computed instead of filtered importance sampling[26].These methods can render caustics,unlike eye-path tracingbased methods(e.g.,cone tracing[27,28]).

However, filtered importance sampling-based VSGL generation induces a flickering error for highfrequency PDFs due to inappropriate kernel sizes.In this paper,we introduce an appropriate kernel size of filtered importance sampling.

3 Modified filtered importance sampling

3.1 Filtered importance sampling

Filtered importance sampling can be used when the integrand has a 2D image f(x),where x∈[0,1]2is the image-space position.This method first samples each kernel center xi∈[0,1]2according to a PDF p(x),and then a filtered value of f(x)is used as each sample value instead of f(xi).This filtered value is given by a pre-filtered mipmap as follows:

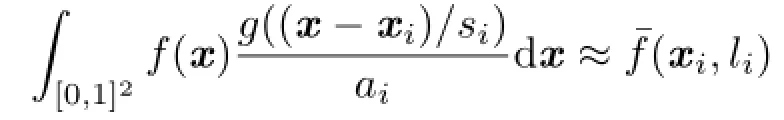
where g((x-xi)/si)is the unnormalized filtering kernel which has a fixed maximum,siis the kernel size,aiis the filtering area(i.e.,normalization factor) given by,andis the mipmapped value of f(x)at mip level li.Let M be the number of texels of f(x),then the filtering area aiis also written as a function of mip level li:Křivánek and Colbert[1]determined mip level liby representing this filtering area using the inverse of the density at sampled center xias

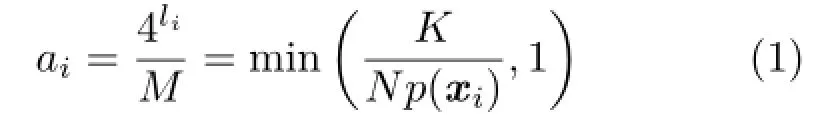
where N is the number of samples,and K is a user-specified parameter to tweak the kernel size (Křivánek and Colbert used K=4).However,this mip level determination is sensitive to the sampled center xi.When xiis at a local minimum of a high-frequency PDF,the filtering kernel can be too large.Conversely,the filtering kernel can also be too small when xiis at a local maximum.Therefore, undesirable overlaps of and gaps between filtering kernels can be produced.

3.2 Our filtering kernels

This paper introduces an appropriate kernel size to reduce overlaps of and gaps between filtering kernels for filtered importance sampling.Sampling according to a PDF is done by computing the inverse cumulative distribution function(CDF)of the PDF. As shown in Fig.2,a sampling interval of the vertical

axis is the integral of the PDF within each filtering kernel.Therefore,if kernel centers are sampled using stratified sampling,this integral is almostHence, an appropriate kernel size siis obtained by solving the following integral equation:

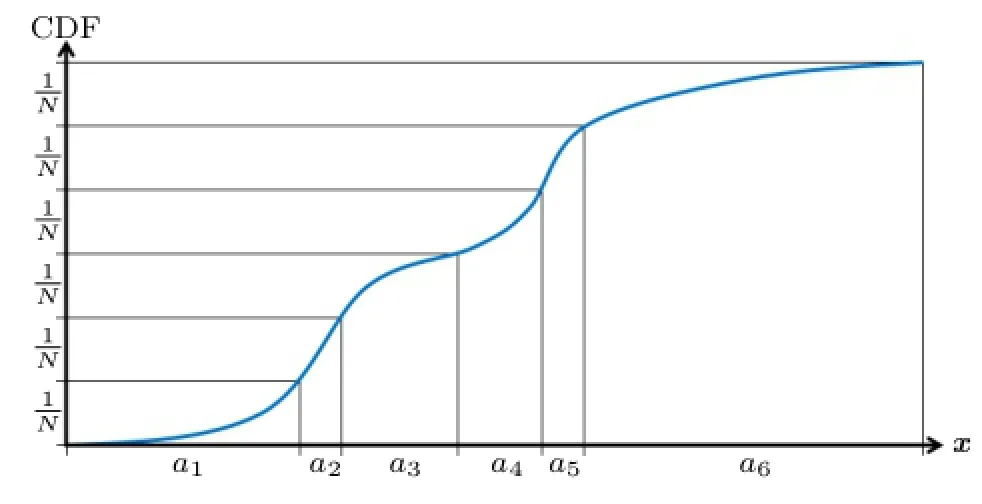
Fig.2 CDF(blue line)and stratified sampled kernels.

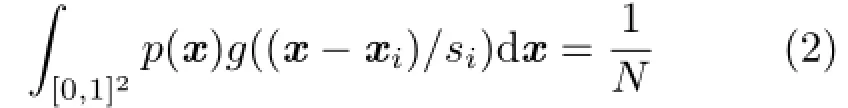
Since the left side is monotonically increasing with respect to the kernel size,we can obtain the kernel size using a bisection method.When PDF p(x) is given by a 2D image,we can use the mipmap of this PDF,which is also used for sampling xivia hierarchical sample warping[12]. Using this mipmap,Eq.(2)is rewritten as

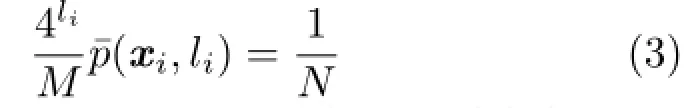
4 Application to virtual spherical Gaussian lights(VSGLs)

In this paper,we demonstrate generation of VSGLs as an effective application of our filtered sampling.A VSGL represents the positional distribution and total radiant intensity of VPLs using a Gaussian and spherical Gaussians,respectively. Since spherical Gaussians have closed-form solutions to evaluate rendering integrals,all-frequency illumination is computed analytically for each VSGL.The VSGL algorithm is composed of the following five phases: reflective shadow map rendering,PDF building, VSGL generation,shadow map rendering,and shading.This paper improves only on the VSGL generation phase.For the detail of VSGLs,please refer to Appendixes A,B,and C.

4.1 Mipmap-based VSGL generation

To generate VSGLs,VPLs are first clustered.Then VPL powers are summed and VPL distributions are averaged for each cluster(Fig.3).To represent VPL distributions with a Gaussian and spherical Gaussians,weighted averages of emission directions, VPL positions,and squared VPL positions weighted by each VPL power are required(for the detail, please refer to Appendix B).Therefore,a reflective shadow map to store the above VPL power and weighted distribution parameters is generated,and then they are mipmapped to approximately obtain total texel values(Fig.4).Let f(x)be the reflective shadow map,then the total texel value within the i th VPL cluster centered at xiis approximated using the mipmapas follows:

Fig.3 Clustered VPLs.Each cluster is approximated with a VSGL by computing the total VPL power and averaged VPL distributions within the cluster.These operations are done by filtered sampling on the reflective shadow map.

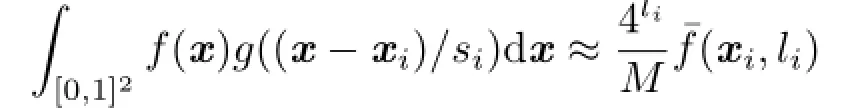
where filtering kernel g((x-xi)/si)represents the VPL cluster.To sample the kernel center xiand mip level li,a filtered importance sampling-based approach can be used. The kernel center xiis sampled according to a dynamic and high-frequency view-dependent PDF p(x)given by the bidirectional reflective shadow mapping method.Tokuyoshi[2] determined liusing Eq.(1)with K=1 according to the previous filtered importance sampling.Using this mip level determination,the total value of reflective shadow map texels within each cluster is given by

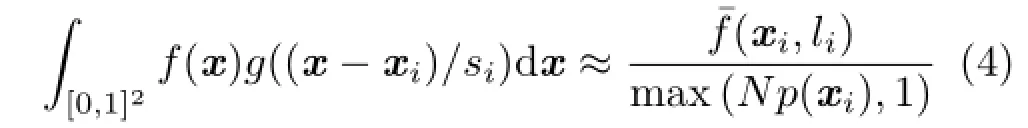
However,since the numerator is filtered while the denominator is not,this sampling method can induce an intensive error due to overlaps of and gaps between filtering kernels.

Fig.4 Mipmapped reflective shadow map for VSGL generation. Average emission directions(c,d)and positions(e,f)are weighted by VPL powers(a,b).VSGLs are sampled from this reflective shadow map based on filtered importance sampling.

4.2 VSGL generation using our filtering kernels

To obtain an appropriate mip level li,this paper employs Eq.(3)instead of Eq.(1)for filtered importance sampling-based VSGL generation.Using this mip level li,the total texel value within each cluster is approximated as follows:

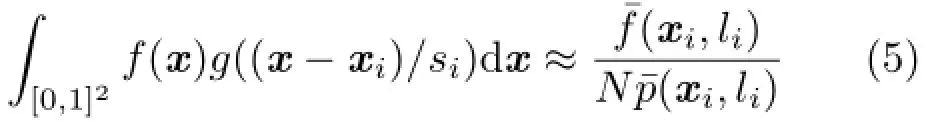
Unlike Eq.(4),both the numerator and denominator are filtered using the same kernel.Hence,temporal coherence is improved for a dynamic high-frequency PDF.Furthermore,the approximation error can be reduced if PDF p(x)is approximately proportional to f(x),similar to standard importance sampling.

Controlling the kernel size.For Eq.(5), the mip level liaffects only the filter bandwidth. Therefore,the user-specified parameter K can also be used for calculating liin our case.This is implemented usinginstead ofin Eq.(3). Using K ＞1,the temporal coherence is improved, though an overblurring error is induced. This overblurring error is reduced by increasing the number of samples N,similar to the original filtered importance sampling.

5 Experimental results

Here we present rendering results using 1024 VSGLs generated using our filtered importance sampling with K=1 on an NVIDIA®GeForce®GTXTM970 GPU.The frame buffer and reflective shadow map(RSM)resolutions are 1920×1088 and 5122, respectively.A tessellation-based imperfect shadow map[15]of resolution 642is employed to evaluate the visibility of each VSGL.To estimate a viewdependent PDF on the reflective shadow map using the bidirectional reflective shadow mapping method, 2048 VSGLs without shadow maps are generated on the G-buffer. For the PDF on the G-buffer, reflectance is used.To perform stratified sampling, the Fibonacci lattice point set using a golden ratio approximation[29]is employed as a quasi-random number.For comparison,this paper uses k-means clustering using 2D image space and 3D world space. In these k-means-based approaches,once clusters are assigned to all the texels,those texels are sorted by cluster ID.Then,to compute the total value of clustered texels,a thread is dispatched for each cluster similar to Prutkin et al.[6].For implementation detail,please refer to Appendix D.

Quality.Figure 5 shows rendered images using different VSGL generation methods. Using the previous kernel size(a),intense artifacts can be produced with low probability,though this sampling method is faster than the k-means-based approaches (c,d).This is because too large of a filtering kernel is produced when the sampled kernel center is at a local minimum of the PDF.On the other hand,our kernel size(b)does not produce these undesirable filtering kernels nor does it noticeably sacrifice performance.

Performance.Table 1 shows the computation time of VSGL generation both for bidirectional reflective shadow mapping(BRSM)(upper row) and final shading(lower row). Our contribution is written in red. Although our method is a numerical approach,its overhead is a total of about five microseconds more compared to the previous filtered importance sampling-based generation.In addition,our method is about 7–9 times faster than the k-means-based approaches. The difference is significant especially for the bidirectional reflective shadow mapping method,which uses a higherresolution G-buffer(1920×1088)than the reflective shadow map(5122).Table 2 shows the computation time using different PDFs. For these PDFs,the performance of k-means-based approaches is more expensive than Table 1.This is because the last pass“Sum”(which is the summation of texel values based on Prutkin et al.’s implementation)has a linear complexity with respect to the number of texels within a cluster.Comparatively,the performance of our approach is almost independent of the PDFs, because it uses pre-filtered mipmaps.Hence,the proposed method is suitable for applications which require stable performance.

Code size. Table 3 shows the code size of VSGL generation in our implementation.Filtered importance sampling-based approaches use only two compute shaders.One is for the calculation of the additional reflective shadow map(or G-buffer),and the other is for the filtered sampling of VSGLs. The difference of our method from the previous method[2]is only the mip level determination(10 lines of code). On the other hand,the k-meansbased approaches require more compute shaders

than ours.In addition,some of them are dispatched iteratively for the GPU sort.Our method is about five times fewer lines of code than the k-means-based approaches.

Fig.5 Rendered images using different VSGL generation methods for 331k-triangle scene(upper row)and 75k-triangle scene(lower row). When a sampled kernel center is at a local minimum of the PDF,the previous method(a)produces too bright of a VSGL with low probability. On the other hand,our method(b)does not produce such an error similar to k-means-based approaches(c,d).Aliasing artifacts on the glossy table in the upper row are the shadow acne of imperfect shadow maps.

Table 1 Computation time of VSGL generation (Unit:ms)

Kernel size controlling.As shown in Fig.6, the kernel size of our method is controllable by using the user-specified parameter K unlike k-means-based approaches.Although some illumination appearance is overblurred by using K＞1,the temporal coherence is improved.The parameter K can be used to balance illumination details and temporal coherence according to the liking of a user.

Table 2 Computation time of VSGL generation (Unit:ms)

Table 3 Code size of VSGL generation(C++and HLSL)

Fig.6 Unlike k-means-based approaches,our approach can control the kernel size using the user-specified parameter K.By increasing K, the temporal coherence is improved,while some illumination appearance is overblurred(262k-triangle scene).

6 Limitations

Feature space. As shown in Fig.7,filtered importance sampling-based approaches(a,b)ignore the difference of world space positions similar to the k-means-based approach using image space(c).If VPLs are clustered ignoring such high-dimensional features,some indirect illumination is blurred when using VSGLs.These low-frequency errors are a limitation of filtered importance samplingbased VSGL generation to achieve real-time frame rates,but they are more visually acceptable than high-frequency artifacts(e.g.,flickering and spiky artifacts).

Fig.7 Light occluded by columns(262k-triangle scene).Since filtered importance sampling-based approaches(a,b)ignore the difference of world space positions similar to the k-means-based approach using image space(c),they blur some indirect illumination for this scene.These low-frequency errors are visually acceptable compared to high-frequency artifacts.

Overlaps and gaps. Although our method reduces overlaps of and gaps between filtering kernels,they cannot be removed completely for inhomogeneous sample distributions.This problem is alleviated by using stratified sampling.

PDF.Since our method requires a given PDF,it cannot be applied to sampling strategies without the PDF(e.g.,sequential Monte Carlo instant radiosity [30]).

Temporal coherence. Since our method improves only the kernel size,kernel centers can still be temporally incoherent for dynamic PDFs. Although the Metropolis–Hastings algorithm can be used for temporally coherent sampling[15],it is limited to static light sources and has a lack of stratification.This problem induces noticeable artifacts especially for caustics(Fig.8).Therefore, this paper employs hierarchical sample warping for stratified sampling. If the temporal coherence is more important than detailed illumination,K ＞1 can be used for our method to improve the temporal coherence.

7 Conclusions

Fig.8 Caustics rendered using our method with the same PDF(514-triangle scene).Kernel centers of the upper row and lower row are generated using hierarchical sample warping[12]and the Metropolis–Hastings-based temporally coherent sampling[15],respectively.Due to a lack of stratification,Metropolis–Hastings produces noticeable artifacts.

This paper improved the kernel size of filtered importance sampling to reduce overlaps of and gaps between filtering kernels.Using this modification for VSGL generation,we are able to render glossy indirect illumination with fewer artifacts than the previous VSGL generation. The overhead of our method is about five microseconds for thousands of VSGLs on a commodity GPU.Although the filtered importance sampling-based approach cannot take into account the difference of higher-dimensional features(e.g.,world position)unlike k-means-based approaches,it is simple,fast,and has stable performance.This paper has demonstrated VSGL-based dynamic glossy indirect illumination,but our method is also usable for spherical Gaussian light generation for dynamic environment maps.Since environment maps are 2D light distribution,it might be more suitable than VSGL generation.We would like to investigate its efficiency in the future.

Appendix A Spherical Gaussians

A spherical Gaussian is a type of spherical function and is represented using a Gaussian function γ with respect to a direction vector ω∈S2as follows:

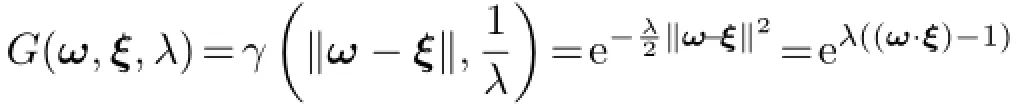
where ξ∈S2is the lobe axis,and λ is the lobe sharpness.ξ andcorrespond to the mean and variance for the Gaussian function,respectively.The integral of a spherical Gaussian is given by

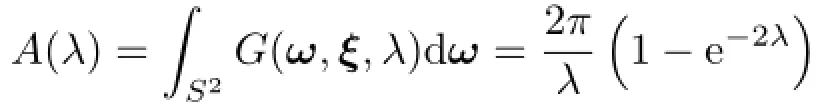
A normalized spherical Gaussianis known as the Von Mises–Fisher distribution.For VSGLs,this distribution is used for representing reflection lobes.

A.1 Spherical Gaussian approximation of reflection lobes

Diffuse lobes.For the Lambert BRDF ρd,the diffuse reflection lobe can be approximated with a spherical Gaussian taking energy conservation into account as follows:

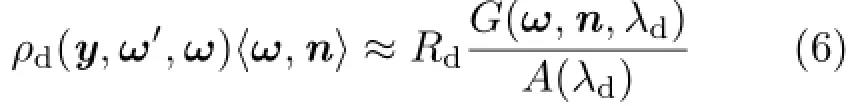
Specular lobes.For the microfacet BRDF ρs, the specular reflection lobe is fitted with a single spherical Gaussian by using Wang et al.’s analytical approximation[22].The BRDF is separated into two factors:the unnormalized normal distribution function D(ωh)whose maximum is one,and the rest of the factors C(ω)as follows:

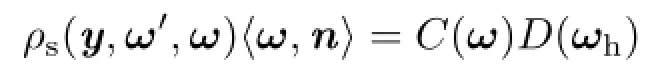
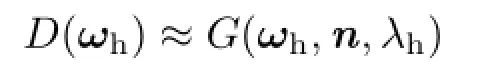
For Beckmann or GGX normal distribution functions,,whereα is the roughness parameter. Using spherical warping,this can be approximated with a function of ω as

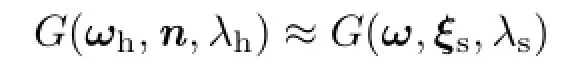
where ξsis the reflection vector given by ξs=2(ω＇·n)n-ω＇,andHence,the specular

lobe is approximated with the following equation:

ρs(y,ω＇,ω)〈ω,n〉≈C(ω)G(ω,ξs,λs)

Moreover,since microfacet BRDFs mostly preserve energy for highly glossy surfaces,the specular lobe can be approximated using a normalized spherical Gaussian as follows:

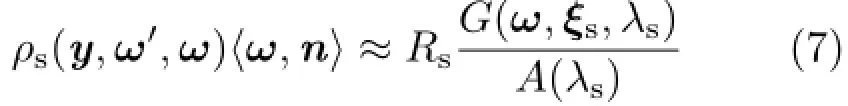
where Rsis the specular reflectance.Anisotropic spherical Gaussians[19]are also usable in the same manner.

Appendix B Virtual spherical Gaussian lights(VSGLs)

This paper approximates a cluster of VPLs with a VSGL.For a VSGL,the total radiant intensity and positional distribution of VPLs are represented using a spherical Gaussian and isotropic Gaussian distribution respectively.This representation can be computed using a simple summation operation.

B.1 Radiant intensity

The radiant intensity of the j th VPL is given as

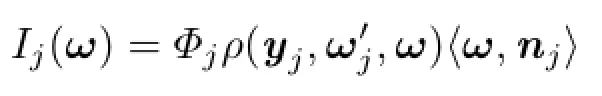
where Φjis the power of the j th photon emitted from the light source,is the incoming direction

of the photon,and nj∈S2is the surface normal at the VPL position yj∈R3,andis the BRDF.This paper first divides this BRDF into diffuse and specular components(i.e.,ρdand ρs). Then,the total radiant intensity of clustered VPLs is approximated with a single spherical Gaussian for each component by using Toksvig’s filtering[35]. For ease of explanation,this subsection hereafter describes only a single BRDF component.The total radiant intensity of a VPL cluster S is represented as

To compute spherical Gaussian parameters cv, ξv,and λvefficiently,each reflection lobe is approximated using Eq.(6)or Eq.(7)as follows:

where Rjis the reflectance,and ξjand λjare the axis and sharpness of the reflection lobe at the j th VPL.Then,the weighted average of the normalized spherical Gaussians weighted by the VPL power ΦjRjis approximated with a single spherical Gaussian as

Using Toksvig’s filtering, the j th normalized spherical Gaussian is first approximately converted into its averaged direction asNext, the weighted average of the directions is computed by

Finally,the filtered spherical Gaussian is obtained from the weighted average direction as,.The coefficient cvis given by cv=

B.2 Positional distribution

In this paper,the positional distribution of VPLs is represented with a single isotropic Gaussian distribution for a VSGL.Unlike radiant intensity, this distribution is not divided into diffuse and specular components in order to avoid the increase of visibility tests(i.e.,shadow maps).The weighted mean of VPL positions is computed by

where Rd,jand Rs,jare the diffuse reflectance and specular reflectance at the j th VPL,respectively. The positional variance is also calculated using weighted average as

Assuming VPLs are distributed on a planar surface, the emitted radiance of a VSGL is represented as follows:

where n is the surface normal which will be eliminated in shading(Section C.1).

B.3 VSGL generation using reflective shadow maps

As mentioned in Sections B.1 and B.2, a VSGL is generated by calculating the total VPL power,total weighted emission direction, total weighted position,and total weighted squared norm of the positionTherefore,these values are stored into reflective shadow maps,and then they are mipmapped to obtain the total values. The i th VPL cluster is represented by the unnormalized filtering kernel g((x-xi)/si)on the reflective shadow map.For example,let f(x)be VPL power stored in the reflective shadow map,then the total VPL power of the i th VPL cluster is given by

We are also able to calculate the total weighted emission direction,total weighted position,and total weighted squared norm of the position in the same manner. In this paper,the image-space position xiand mip level liare sampled based on filtered importance sampling.

Appendix C Shading

For each shading point ypwith view direction ωp,the reflected radiance is calculated using the rendering equation[36]defined by

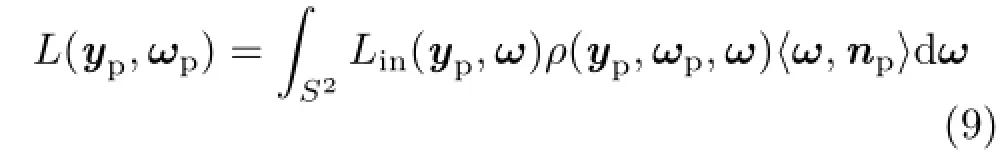
where Lin(yp,ω)is the incoming radiance,and npis the surface normal at the shading point.This paper approximates the incoming radiance using spherical Gaussians for the analytical approximation of the rendering integral[19,22].

C.1 Incoming radiance

Using Eq.(8),the approximated incoming radiance is given by

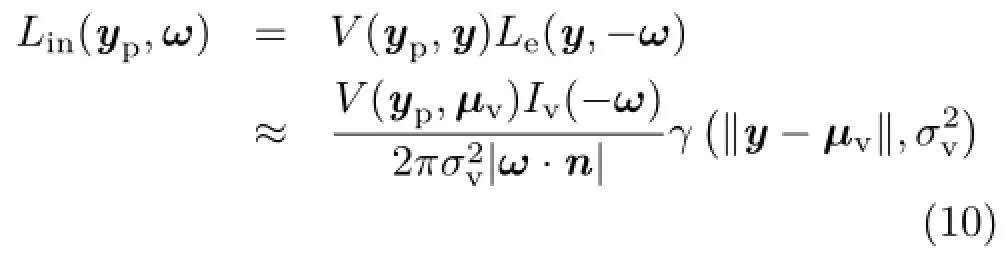
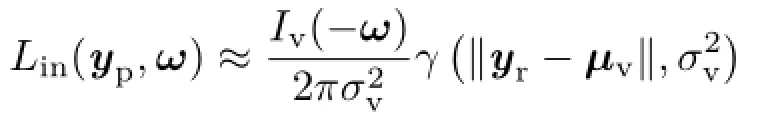
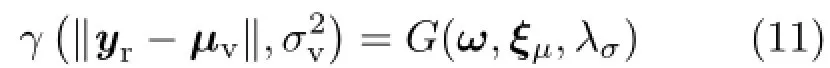
the VSGL viewed from yp.Using Eq.(11),the incoming radiance is approximated with the product of two spherical Gaussians which yields a spherical Gaussian as follows:

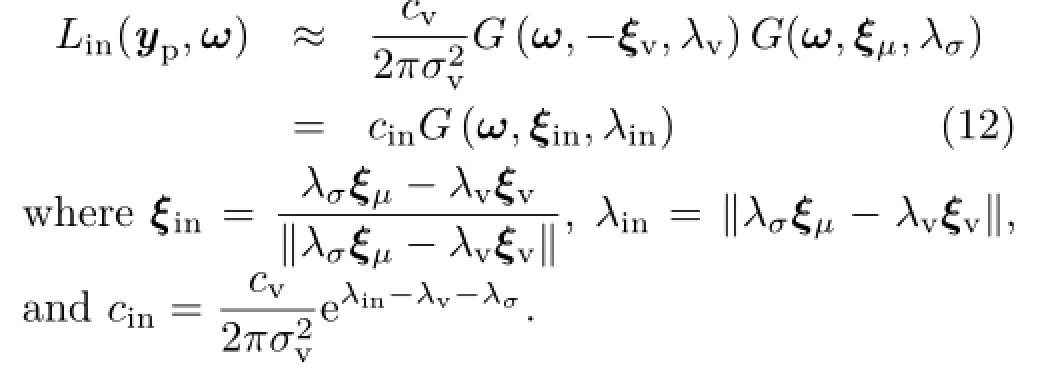
C.2 Shading via product integrals of spherical Gaussians

Since the reflection lobe ρ(yp,ωp,ω)〈ω,np〉can be approximated using spherical Gaussians and anisotropic spherical Gaussians,Eq.(9)can be calculated using the analytical product integral.

Diffuse reflection. Using Eq.(6)and Eq.(12), the rendering integral of the diffuse component is calculated using the analytical product integral of two spherical Gaussians.This approach is efficient for a few VSGLs[26].However,a light leak error caused by the spherical Gaussian approximation of reflection lobes cannot be reduced by increasing the number of VSGLs.Unlike the secondary bounce represented by VSGLs,light leaks are noticeable at the first bounce which is more visually important. Therefore,for thousands of VSGLs,the cosine factor at the first bounce is assumed to be a constant and pulled out of the integral[22]as follows:

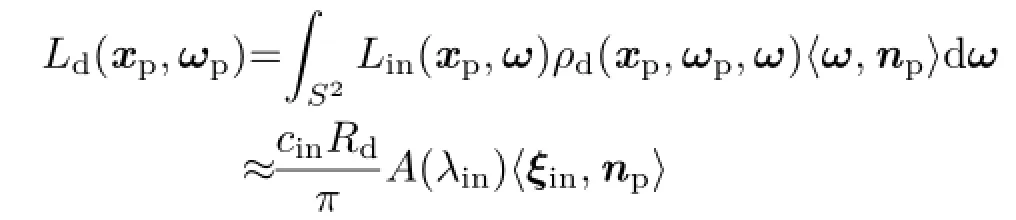
In addition,when λinis not small,can be assumed[20].Therefore,diffuse reflection is inexpensively calculated using the following equation:

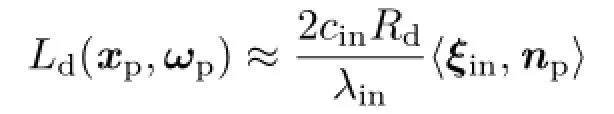
Specular reflection.While spherical Gaussians are used for VSGLs,this paper employs an anisotropic spherical Gaussian to approximate a specular lobe at a shading point.This is because a specular lobe can be anisotropic even if it is an isotropic BRDF model,especially for shallow grazing angles.For simplicity,anisotropic spherical Gaussians are used only for the first bounce which is more visually important than the second bounce. In addition,the product integral of a spherical Gaussian and anisotropic spherical Gaussian[19] has a reasonable computation cost.An anisotropic spherical Gaussian is defined as

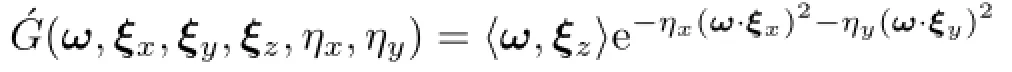
where ξx,ξy,ξzare orthonormal vectors,and ηx, ηyare the bandwidth parameters.Since a specular lobe is approximated with an anisotropic spherical Gaussian as, ξy,ξz,ηx,ηy),the rendering integral is calculated as

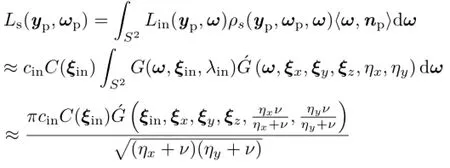
Appendix D Implementation details of VSGL generation

VSGL generation using filtered importance sampling. Our implementation is based on Tokuyoshi[2],and uses DirectX®11.After rendering a reflective shadow map,an additional reflective shadow map(which stores VPL positions,squared VPL positions,and average emission directions to calculate VSGL parameters)is generated using a compute shader. Then,these reflective shadow maps are mipmapped using a graphics API(i.e., GenerateMips of DirectX).Finally,VSGLs are generated based on filtered importance sampling. The proposed mip level liis calculated using Algorithm 1.

Algorithm 1 Mip level calculation using the bisection method lmin←0 lmax←the top mip level offor k=1 to the user-specified iteration count do l←(lmin+lmax)/2 if 4lN then lmin←l else l max←l end if end for li←(lmin+lmax)/2 M(xi,l)＜K

VSGL generation using k-means. For comparison,this paper uses k-means VPL clustering using 2D image space and 3D world space.The k-means algorithm first samples the cluster center according to the PDF,and then the closest center is computed for each VPL.In our implementation, all the texels are assigned to clusters for highfrequency geometries and textured glossy materials unlike Dong et al.[5].To accelerate the search of the closest cluster center for each texel,a kd-tree of cluster centers is built using parallel construction of a binary radix tree[38].For densely distributed cluster centers,this tree-based search is more efficient than using a 2D uniform grid proposed by Prutkin et al. [6].Once clusters are assigned to all the texels,those texels are sorted by cluster ID.Then,to compute the total value of clustered texels,a thread is dispatched for each cluster similar to Prutkin et al.[6].Unlike Prutkin et al.,we use a GPU radix sort[39]instead of bitonic sort for the high-resolution reflective shadow map and G-buffer. Although k-means clustering can be improved by updating cluster centers in an iterative fashion,we do not update iteratively in this paper.

Acknowledgements

The polygon models are courtesy of M.Dabrovic, F.Meinl,A.Grynberg,and G.Ward.The author would like to thank the anonymous reviewers for valuable comments and helpful suggestions.

[1]Křivánek,J.；Colbert,M.Real-time shading with filtered importance sampling.Computer Graphics Forum Vol.27,No.4,1147–1154,2008.

[2]Tokuyoshi, Y.Virtual spherical Gaussian lights for real-time glossy indirect illumination.Computer Graphics Forum Vol.34,No.7,89–98,2015.

[3]Dachsbacher,C.；Stamminger,M.Reflective shadow maps.In:Proceedings of the 2005 Symposium on Interactive 3D Graphics and Games,203–231,2005.

[4]Keller,A.Instant radiosity.In:Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques,49–56,1997.

[5]Dong,Z.；Grosch,T.；Ritschel,T.；Kautz,J.；Seidel, H.-P.Real-time indirect illumination with clustered visibility.In:Proceedings of the Vision,Modeling,and Visualization Workshop,187–196,2009.

[6]Prutkin,R.；Kaplanyan,A.S.；Dachsbacher,C. Reflective shadow map clustering for real-time global illumination.In:Proceedings of Eurographics 2012 (Short Papers),9–12,2012.

[7]Ritschel,T.；Grosch,T.；Kim,M.H.；Seidel,H.-P.；Dachsbacher,C.；Kautz,J.Imperfect shadow maps for efficient computation of indirect illumination.ACM Transactions on Graphics Vol.27,No.5,Article No. 129,2008.

[8]Agarwal,S.；Ramamoorthi,R.；Belongie,S.；Jensen, H.W.Structured importance sampling of environment maps.ACM Transactions on Graphics Vol.22,No.3, 605–612,2003.

[9]Debevec,P.A median cut algorithm for light probe sampling.In: Proceedings of SIGGRAPH 2005 Posters,Article No.66,2005.

[10]Ritschel,T.；Eisemann,E.；Ha,I.；Kim,J.D. K.；Seidel,H.-P.Making imperfect shadow maps viewadaptive:High-quality global illumination in large dynamic scenes.Computer Graphics Forum Vol.30, No.8,2258–2269,2011.

[11]Dachsbacher,C.；Křivánek,J.；Hašan,M.；Arbree,A.；Walter,B.；Novák,J.Scalable realistic rendering with many-light methods.Computer Graphics Forum Vol. 33,No.1,88–104,2014.

[12]Clarberg,P.；Jarosz,W.；Akenine-Möller,T.；Jensen, H.W.Wavelet importance sampling: Efficiently evaluating products of complex functions.ACM Transactions on Graphics Vol.24,No.3,1166–1175, 2005.

[13]Dachsbacher,C.；Stamminger,M.Splatting indirect illumination.In:Proceedings of the 2006 Symposium on Interactive 3D Graphics and Games,93–100,2006.

[14]Ritschel,T.；Dachsbacher,C.；Grosch,T.；Kautz,J. The state of the art in interactive global illumination. Computer Graphics Forum Vol.31,No.1,160–188, 2012.

[15]Barák,T.；Bittner,J.；Havran,V.Temporally coherent adaptive sampling for imperfect shadow maps.Computer Graphics Forum Vol.32,No.4,87–96,2013.

[16]Křivánek,J.；Ferwerda,J.A.；Bala,K.Effects of global illumination approximations on material appearance.ACM Transactions on Graphics Vol.29, No.4,Article No.112,2010.

[17]Luksch,C.；Tobler,R.F.；Habel,R.；Schwärzler, M.；Wimmer,M.Fast light-map computation with virtual polygon lights.In:Proceedings of the ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games,87–94,2013.

[18]Tsai,Y.-T.；Shih,Z.-C.All-frequency precomputed radiance transfer using spherical radial basis functions and clustered tensor approximation.ACM Transactions on Graphics Vol.25,No.3,967–976, 2006.

[19]Xu,K.；Sun,W.-L.；Dong,Z.；Zhao,D.-Y.；Wu,R.-D.；Hu,S.-M.Anisotropic spherical Gaussians.ACM Transactions on Graphics Vol.32,No.6,Article No. 209,2013.

[20]Iwasaki,K.；Dobashi,Y.；Nishita,T.Interactive

bi-scale editing of highly glossy materials.ACM Transactions on Graphics Vol.31,No.6,Article No. 144,2012.

[21]Iwasaki,K.；Mizutani,K.；Dobashi,Y.；Nishita, T.Interactive cloth rendering of microcylinder appearance model under environment lighting. Computer Graphics Forum Vol.33,No.2,333–340, 2014.

[22]Wang,J.；Ren,P.；Gong,M.；Snyder,J.；Guo,B. All-frequency rendering of dynamic,spatially-varying reflectance.ACM Transactions on Graphics Vol.28, No.5,Article No.133,2009.

[23]Xu,K.；Ma,L.-Q.；Ren,B.；Wang,R.；Hu,S.-M.Interactive hair rendering and appearance editing under environment lighting.ACM Transactions on Graphics Vol.30,No.6,Article No.173,2011.

[24]Yan,L.-Q.；Zhou,Y.；Xu,K.；Wang,R.Accurate translucent material rendering under spherical Gaussian lights.Computer Graphics Forum Vol.31, No.7,2267–2276,2012.

[25]Xu,K.； Cao,Y.-P.； Ma,L.-Q.； Dong,Z.；Wang,R.；Hu,S.-M.A practical algorithm for rendering interreflections with all-frequency BRDFs. ACM Transactions on Graphics Vol.33,No.1,Article No.10,2014.

[26]Tokuyoshi,Y.Fast indirect illumination using two virtual spherical Gaussian lights.In:Proceedings of SIGGRAPH Asia 2015 Posters,Article No.12,2015.

[27]Crassin,C.；Neyret,F.；Sainz,M.；Green,S.；Eisemann,E.Interactive indirect illumination using voxel cone tracing.Computer Graphics Forum Vol.30, No.7,1921–1930,2011.

[28]Xu,C.；Wang,R.；Bao,H.Realtime rendering glossy to glossy reflections in screen space.Computer Graphics Forum Vol.34,No.7,57–66,2015.

[29]Sloan,I.H.；Joe,S.Lattice Methods for Multiple Integration.Oxford University Press,1994.

[30]Hedman,P.；Karras,T.；Lehtinen,J.Sequential Monte Carol instant radiosity.In:Proceedings of the 20th ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games,121–128,2016.

[31]Blinn,J.F.Models of light reflection for computer synthesized pictures.ACM SIGGRAPH Computer Graphics Vol.11,No.2,192–198,1977.

[32]Beckmann,P.；Spizzichino,A.The Scattering of Electromagnetic Waves from Rough Surfaces.New York:MacMillan,1963.

[33]Trowbridge,T.S.；Reitz,K.P.Average irregularity representation of a rough surface for ray reflection. Journal of the Optical Society of America Vol.65,No. 5,531–536,1975.

[34]Walter,B.；Marschner,S.R.；Li,H.；Torrance,K. E.Microfacet models for refraction through rough surfaces.In:Proceedings of the 18th Eurographics Conference on Rendering Techniques,195–206,2007.

[35]Toksvig,M.Mipmapping normal maps.Journal of Graphics Tools Vol.10,No.3,65–71,2005.

[36]Kajiya, J.T.The rendering equation.ACM SIGGRAPH Computer Graphics Vol.20,No.4,143–150,1986.

[37]Hašan,M.；Křivánek,J.；Walter,B.；Bala,K.Virtual spherical lights for many-light rendering of glossy scenes.ACM Transactions on Graphics Vol.28,No. 5,Article No.143,2009.

[38]Karras,T.Maximizing parallelism in the construction of BVHs,octrees,and k-d trees.In:Proceedings of the 4th ACM SIGGRAPH/Eurographics Conference on High-Performance Graphics,33–37,2012.

[39]Merrill,D.G.；Grimshaw,A.S.Revisiting sorting for GPGPU stream architectures.In:Proceedings of the 19th International Conference on Parallel Architectures and Compilation Technique,545–546, 2010.

Yusuke Tokuyoshi is a senior researcher at Square Enix.He received his Ph.D.degree in engineering from Shinshu University in 2007.Before joining Square Enix,he engaged in R&D on compiler optimization at Hitachi,Ltd. His interests include global illumination algorithms and real-time rendering.

Open Access The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License(http:// creativecommons.org/licenses/by/4.0/), which permits unrestricted use,distribution,and reproduction in any medium,provided you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons license,and indicate if changes were made.

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript,please go to https://www. editorialmanager.com/cvmj.

© The Author(s)2016.This article is published with open access at Springerlink.com