降低解析几何运算量的几种技巧

王昊渊

降低解析几何运算量的几种技巧

王昊渊

解析几何题的运算式子复杂，运算量大，往往成为学生失分的重要因素。在学习过程中，笔者认为要解决失分问题，就必须使运算的式子简便，降低运算量。由此，总结了解决这个问题的几种技巧。

一、善于设点的坐标

设点的坐标是解题中常用的方式。设得好，设得巧，可以使运算式子简便，降低运算量。

（1）当k=0时，分别求C在点M和N处的切线方程；

（2）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由。

因此，x1+x2=4k，x1x2=-4a。

假设存在点P（0，b），使得当k变动时，总有∠OPM=∠OPN，则由角平分线定理，得

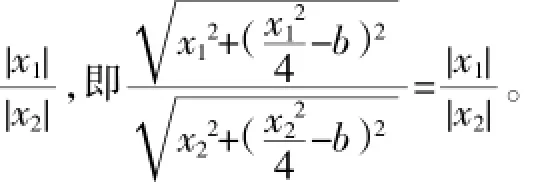
当b=a时，唯有k=0时成立，故舍去。所以b=-a，故y轴上存在点P（0，-a），使得当k变动时，总有∠OPM=∠OPN。

二、巧用平面几何定理

平面几何中涉及的线、角、面积的大小关系都可以用几何等式来表达，没有代数运算的繁杂。利用平面几何知识找出题中的平行、垂直、全等、相似关系，可以缩短思考的过程，然后用坐标表示，也能达到减少运算量的目的。因此，将平面几何中的一些定理用到解析几何中，是减少解析几何运算量常用的技巧。

（1）求△OAB面积的最小值；

（2）过点O作AB的垂线，垂足是P，求点P的轨迹方程。

因此，cos2β=sin2α，sin2β=cos2α。

显然，当sin2α=0，α=0°时，有最小值

（2）先证一个结论。

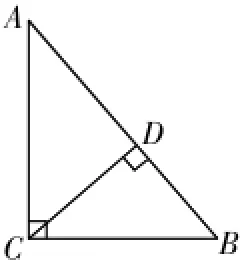
在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，则

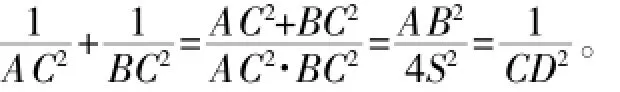
故点P的轨迹方程是x2+y2=。

三、妙用圆锥曲线的几何性质

圆锥曲线的定义（两种）、焦半径、离心率、准线以及a，b，c等有十分明确的几何意义，如果能够恰当地将几何意义应用到解题中，可以简化许多复杂的运算，还容易找到解题思路。

设椭圆的右顶点为A，并设∠AFPi=α（ii=1，2，3）。不失一般性，设，且设点P（ii=1，2，3）在l上的射影为Q（ii=1，2，3）。

减少解析几何运算量的方法还有一些，如整体代换、坐标变换、运用参数方程与极坐标方程等。解题时，要仔细分析条件与待求（证）式子的特点，选择合适的方法，才能达到事半功倍的效果。

（作者单位：湖南师范大学附中梅溪湖中学）