混合分布下带干扰的多险种负风险模型*

闭盟华，方世祖，覃利华

(广西大学 数学与信息科学学院,广西 南宁 530004)



混合分布下带干扰的多险种负风险模型*

闭盟华，方世祖，覃利华

(广西大学 数学与信息科学学院,广西 南宁 530004)

考虑混合分布的带干扰多险种风险模型，运用风险理论及随机过程理论的知识得到该模型的盈利过程的期望、方差、矩母函数、独立平稳增量性、调节系数以及用鞅方法得到该模型的最终破产概率及其破产概率满足的Lundberg不等式.

混合分布；负风险模型；盈利过程；最终破产概率；矩母函数;调节系数；鞅; Lundberg不等式

针对近年保险公司保险业务的蓬勃发展，保险品种越发多样化，同时公司的经营还受到其他不确定因素的影响，传统经典的负风险模型[1-3]已经不能满足现实的需求，之前带干扰的单或双险种的负风险模型[4-10]日益受到学者的重视研究及推广.为了更加贴近实际,文章在总结现有研究的基础上,针对现实中保险公司各种寿险理财产品的“理赔”次数过程的期望与方差的三种大小关系，继续讨论一类混合分布下带干扰的多险种负风险模型，其中混合分布为一险种的“理赔”次数服从负二项分布，另一险种的“理赔”次数服从二项分布,第三个险种的“理赔”次数服从poisson分布;在此先给出二项随机序列和负二项随机序列以poisson随机过程的定义，接着再给出混合分布下带干扰的多险种负风险模型.

定义1 非负整数随机序列{P(n),n=0,1,2,…}中，P(0)=0,且对于任意n1>n2,增量P(n1)-P(n2)服从参数为(n2-n1,p)的二项分布,则称序列{P(n),n=0,1,2,…}为二项随机序列.其期望E(P(n))=npX,方差Var(P(n))=npxqY,矩母函数为MP(t)=(pXet+qX)n,且二项序列“理赔”次数过程的均值大于方差.

定义3 如果计数过程{R(t),t≥0}具有参数θ(θ>0)和独立平稳增量性,并且同时满足R(0)=0和E[R(t)]=θt,则称其为poisson过程,poisson随机序列的“理赔”次数过程的均值等于方差,其期望E(R(t))=θ,方差Var(R(t))=θ,矩母函数为MR(t)=exp[θ(et-1)].

下面给出混合分布带干扰多险种负风险模型：

(1)

其中

2)保险公司单位时间支出为常数c>0;

3)i,j,k和n均取非负整数;初始资本为常数u≥0;

4)零初值二项序列{P(n),n≥0}服从参数(n,pA)，{Q(n),n≥0}为服从参数(n,pB)的零初值负二项序列，{R(n),n≥0}是强度为θ的poisson过程;

5){Xi,i≥1},{Yj,j≥1},{Zk,k≥1}是独立同分布的非负理赔额随机序列，均值分别为η1、η2和η3，分布函数为F(x)、F(y)、F(z)，二阶矩都存在.

6)随机干扰项ε{T(n),n=1,2,3,…}为标准布朗运动,代表不确定收益;

7)假定{P(n),n≥0}，{Q(n),n≥0}，{Xi,i≥1}，{Yj,j≥1}，{Zk,k≥1}，{T(n),n≥0}相互独立;

注:上述负风险模型(1)在实际应用中,可用Xi表示某地区青年人寿险年金保险的第i次“理赔”额,Yj表示某地区中年人寿险年金保险的第j次“理赔”额,Zk表示某地区老年人寿险年金保险的第k次“理赔”额.

引理 上述带干扰负风险模型(1)的盈利过程{S(n),n≥0}具有以下性质:

1){S(n),n≥0}是独立的平稳增量过程,且S(n)→∞ a.s.(n→+∞);

2){S(n),n≥0}的期望、方差、矩母函数分别为：

其中Var[X]=δ1,Var(Y)=δ2,Var(Z)=δ3,qX=1-pX,qY=1-pY.

证明:1)先证明独立性.对于任意的0≤n1≤n2≤n3≤…≤ns,0≤r≤s,

再证平稳性.对给定的l≥1,

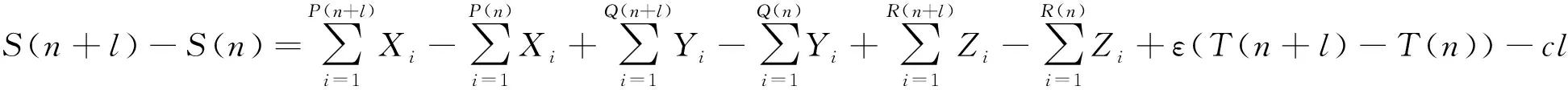
综上可知，{S(n),n≥0}是平稳独立增量过程.

2)由随机过程论相关知识及假定7)中的独立性可知:

定理1 存在函数l(t)在盈利过程{S(n),n≥0}上满足E[exp(-tS(n))]=exp(nl(t)).

证明:E[exp(-tS(n))]

定理2 在其定义区间(0,b)内方程l(t)=0存在唯一正解t=R，R称为调节系数.

证明:观察方程l(t)=0，

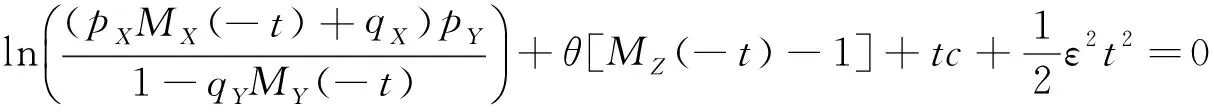
知MX(0)=1,MY(0)=1,MZ(0)=1,

此时方程(2)恒成立.即l(0)=0

(2)

现对函数l(t)对t求导，有

(3)

l″(t)

(4)

由(2)、(3)、(4)结合数学分析的函数相关性质可知，函数l(t)在[0,+∞)上是下凸函数且存在唯一正解R,定理得证.

证明：关于F为鞅的证明可分3步:

1)显然指数函数是F可测的,而U(t)是建立在完备的概率空间(Ω,F,P)上的F可测函数,故复合函数G(t)=exp[-RU(t)]也F可测.

2)E[G(t)]=E{exp[-RU(t)]}=exp(-Rt)E{exp[-RS(t)]} =exp(-Rt)<1<+∞,∀t≥0.

3)对任意的0≤s

E[G(t)|Fs]=E[exp{-R[u+S(t)]}|FS] =E[exp{-R[u+S(t)+S(s)-S(s)]}|FS] =exp{-R[u+S(s)]}E[exp{-R[S(t)-S(s)]}|FS] =G(s)E[exp{-R[S(t)-S(s)]}|FS]=G(s)

综上所述，由随机过程论中连续参数鞅的定义可知{G(t);t≥0}关于F的鞅.

下面用两种方法求带干扰的混合分布多险种负风险模型(1)的最终破产概率τ(u).

方法1:鞅方法

由定理3前部分关于G(t)为鞅的证明可知G(t)=e-RU(t)=G(0)e-RS(t)为非负鞅,由非负鞅收敛性定理知存在几乎处处收敛的有限极限使得

取定t,由于破产时刻T为有界停时，则T∧t也为有界停时,由鞅的可选抽样定理知

E[G(T∧t)]=E[G(0)]=e-Ru,对e-Ru用全期望公式,有

e-Ru=E[G(T∧t)]=E[G(T∧t|T≤t)]P{T≤t}+E[G(T∧t)|T>t]P{T>t} =E[G(T)|T≤t]P{T≤t}+E[G(t)|T>t]P{T>t}.

又∀m0,故G(m)=e-RU(m)<1<+∞,由Lebesgue控制收敛定理和单调收敛定理有,e-Ru=E[G(T<+∞)|T<+∞]P{T<+∞}+E[G(+∞)|T=+∞]P{T=+∞}

E[G(+∞)|T=+∞]P{T=+∞}=0,于是 e-Ru=E[G(T<+∞)|T<+∞]P{T<+∞}

又 τ(u)=P{T<+∞|U(0)=u}=P{T<+∞},G(T<+∞)=G(T)=e-RU(T)，所以有

E(U(n))=φ1n+u,Var(U(n))=φ2n

(5)

分别服从参数为(n-H,pX),(n-H,pY),(θ-H)n的二项分布,负二项分布,poisson分布,且

于是对任意n,t>0,

E[e-tU(H)]=E[e-tU(H)|H>n]P(H>n)+E[e-tU(H)|H≤n]P(H≤n)=H1+H2

(6)

Ω(n)>0,且易知U(n)>Ω(n).

将H1拆成两项讨论,即

H1=E[e-tU(H)|H>n]P(H>n)=E[e-tU(H)|H>n,U(n)>Ω(n)]P(H>n,U(n)>Ω(n))+E[e-tU(H)|H>n,0≤U(n)≤Ω(n)]P(H>n,0≤U(n)≤Ω(n))≤P(0≤U(n)≤Ω(n))+e-tΩ(n)

(7)

再由切比雪夫不等式，有

于是由夹逼定理及(7)式可知,

H1=E[e-tU(H)|H>n]P(H>n)→0,(n→+∞)

(8)

令t=调节系数R,则

E[e-RU(n)]=E[e-RU(H)|H>n]P(H>n)+E[e-RU(H)|H≤n]P(H≤n)

(9)

当n充分大时,(9)式右边第二项可化为E[e-RU(H)|H<∞]P(H<∞)

即 E[e-RU(n)]=E[e-RU(H)|H>n]P(H>n)+E[e-RU(H)|H<∞]P(H<∞)

(10)

结合(8)式和(10)式及τ(u)=P{T<+∞|U(0)=u}=P{T<+∞}知，该风险模型的最终破产概率为:

推论 注意到U(H)<0,R>0,于是

故τ(u)≤e-Ru,∀u≥0.

即混合分布下带干扰的多险种负风险模型(1)的最终破产概率满足

Lundberg不等式τ(u)≤e-Ru,∀u≥0，证毕.

[1]Grandel J.aspects of risk theorey[M].New York:Springer-Verlag,1991:4-11.

[2]林元煭.应用随机过程[M].北京:清华大学出版社,2002.

[3]成世学.破产论研究综述[J].数学的进展,2002,31(5).

[4]Chen Hongyan,Liu Wei.The ruin probability of a kind of promoted two-type-risk compound poisson risk model[J].J.of Math.(PRC),2009,29(2):201-205.

[5]李应求,甘柳,魏民.一类多险种复合Poisson-Geometric过程风险模型研究[J].统计与决策,2010(7).

[6]Luo Kui,Hu Yijin.The negative risk model with the compound binomial process[J].J.Math.(PRC),2009,29(10):409-412.

[7]蒋志明,王汉兴.一类多险种风险过程的破产概率[J].应用数学与计算数学学报,2000(1):9-16.

[8]董迎辉,王过京.常利率下带干扰负风险模型的破产概率[J].应用数学学报,2010,33(1):88-94.

[9]方世祖,黄鸿君,陈流红.保费随机收取下带特殊分红策略的复合二项风险模型[J].数学理论与应用.2014,3(3-8).

[10]方世祖,陈流红,郭梦丹,等.离散时间的双险种风险模型研究[J].广西科学院学报,2015,31(1):54-58.

[11]Avanzi B.& Gerber H.U.Optimal dividend in the dual model with diffusion[J].ASTIN Bulletin,2008,38(2)：653-667.

[责任编辑 苏 琴] [责任校对 黄祖宾]

A Negative Risk Model Perturbed by Diffusion with Mixed Distribution

BI Meng-hua,FANG Shi-zu,QIN Li-hua

(SchoolofMathematicsandInformationSciences,GuangxiUniversity,Nanning530004,China)

In this paper,we consider the distribution of the hybrid multiple risk model with interference,risk theory and random process theory knowledge get the expectation and variance of the process model of profit,the moment generating function,smooth independent incremental,adjustment coefficient and the ultimate ruin probability of the model and meet the Lundberg inequality.

Mixed distribution; Negative risk model; Earnings process; The final bankruptcy probability; Moment generating function ;The adjusting coefficient; martingale; Lundberg inequality

2016-03-10.

国家自然科学基金项目(71462002)；广西教育厅科研项目(201010LX004).

闭盟华(1984-),男,广西南宁人,广西大学在校研究生,研究方向：随机过程在风险理论中的应用.

方世祖(1964-),男，广西武鸣人，广西大学硕士生导师，研究方向：随机过程在风险理论中的应用.

O211.67

A

1673-8462(2016)03-0059-06