关于多险种初始资本分配策略的研究

曲忠宪，武文华，王春红

(海南热带海洋学院海洋信息工程学院，海南三亚572022)

1 经典破产理论模型

破产论具有代表性的几个研究方向．完全离散经典风险模型的研究［1～2］;重尾部分布破产论的研究［3］;具有投资收益破产论的研究［4］;保险数学与金融数学交叉的研究［5～6］;随机投保费下多险种破产模型的研究［7～8］．

设保险公司在时刻t的盈余为

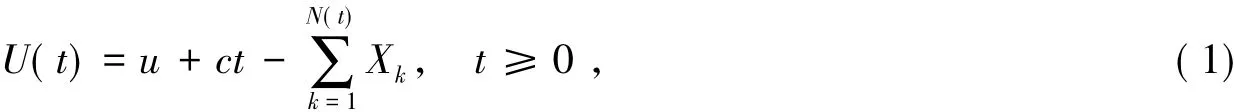
其中:u为初始资本;c为保险公司单位时间征收的保险费率;Xk(k≥1)为第k次索赔额;N(t)为到时刻t为止发生的索赔次数;称公式(1)为经典破产模型．

假设{Xk:k≥1}是独立同分布于X的变量序列，记X的分布函数为F(x)，数学期望为μ;{N(t):t≥0}是以λ为强度的泊松过程;{Xk:k≥1}与{N(t):t≥0}相互独立．保险公司为了保证安全，要求cλμ ＞ 0．

盈余过程有可能取负值，这时称保险公司“破产”．以下恒记T为保险公司首次破产的时刻，简称为破产时刻，即令T=inf{t:U(t)＜0}．

记最终破产概率为Ψ(u)，则Ψ(u)=P(T＜"U(0)=u)．

假设个体索赔额的矩母函数

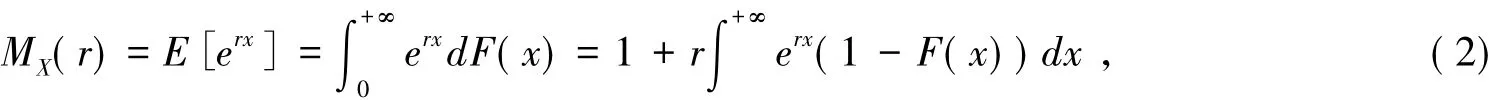
至少在包含原点的某个邻域内存在，并且下述方程

具有正解．方程(3)若有正根，必是唯一的，记正根为R并称其为调节系数．

定理1［9］若上述假设成立，则有Ψ(u)≤e－Ru，u≥0．

2 经典破产理论模型的推广

在文献［10］中，将经典风险模型(1)推广到多险种破产模型(4)得到了下面的定理2．

设保险公司在时刻t的盈余为

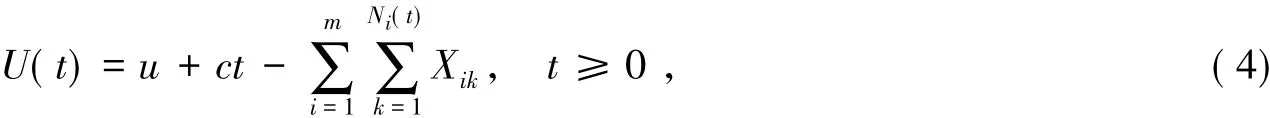
其中为保险公司单位时间征收的保险费率;ci为第i个险种单位时间征收的保险费率;Xik为第i个险种的第k次索赔额;Ni(t)为至时刻t为止第i个险种发生的索赔次数．

假设{Xik:k≥1}是独立同分布于Xi的随机变量序列，记Xi的分布函数为Fi(x)，数学期望为μi＞是以λi为参数的Poisson过程;{Xik:k≥1}与{Ni(t):t≥0} 相互独立;各{Xik:k≥1}，i=1，2，…，m相互独立;各{Ni(t):t≥0}，i=1，2，…，m相互独立;各个调节系数Ri存在且唯一．

保险公司为了保险起见，对于第i险种要求ci－λiμi＞0，因此即单位时间平均获利大于零．

以下恒记T为保险公司首次破产的时刻，即令T=inf{t:U(t)＜0}，最终破产概率记为φ(u)，则φ(u)=P(T ＜"U(0)=u)．

设Mi(r)是变量Xi的矩母函数，函数－rc，则有如下定理．

定理2 破产模型(4)的最终破产概率φ(u)≤e－Ru，其中R是方程h(r)=0的唯一正根，u是初始资本．

3 多险种初始资本分配策略

保险公司有m个险种，每个险种独立经营，自负盈亏．u是初始资本，ci是第i个险种的单位时间征收的保险费率．问题:能否提供较优的分配初始资本u的策略，使关心的险种最终破产的概率都小于等于一个小正数．

设0＜α ＜ 1，对于第i(i=1，2，…，m)个险种应用定理1，令其中:Ri为调节系数是方程λiMi(r)=λi+cir的正根．求解不等式(5)可得:

3．1 如果，则第i(i=1，2，…，m) 个险种初始资金分配即可，可以保证第i个险种最终破产的概率φi(vi)≤α，i=1，2，…，m;此时初始资本有结余额面讨论如何将M追加到这m个险种之中．

3．1．1 加权平均的分配策略

取以 k1，k2，…，km为权来分配余额 M．令

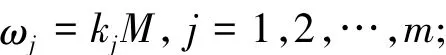
其中:ωj为追加到第j个险种的资本，从而第j个险种的初始资本为uj=vj+ωj．故第j险种最终破产概率φj(vj+ ωj) ≤ e－Rj(vj+ωj)≤ α，j=1，2，…，m．

3．1．2 减少α的值到达α0的分配策略

令方程

求方程(7)的解α0，可知

从而第i个险种追加

故第i(i=1，2，…，m)个险种分配到初始资金时，就能使各个险种破产的概率都小于等于α0．

显然，分配策略 3．1．1 与 3．1．2 是一致的．

3．2 如果，那么有可能满足不了使每个险种最终破产的概率都小于等于α，因此必须再注入资本下面给出没有资本可以注入的条件下，如何分配初始资本u．

3．2．1 序下的分配策略

将m个险种按平均单位时间的获利由大到小排序，比如排序为第i1，i2，…，im险种，即cik－λikμik≥cij－ λijμij，1 ≤ k ＜ j≤ m．按照公式

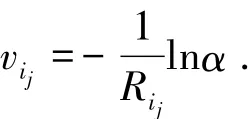
可以算出vi1，vi2，…，vim的值，这些数从左到右累加，求出使得下式成立的k，

于是保险公司优先经营第i1，i2，…，ik险种，考虑放弃其它m－k个险种的经营．

3．2．2 预留储备资金的分配策略

从初始资本 u中取出储备资金 u0，记调节系数 R1，R2，…，Rk中的最小的数为 R(1)，并且假定．将资本u－u0分配到每个险种中，令函数

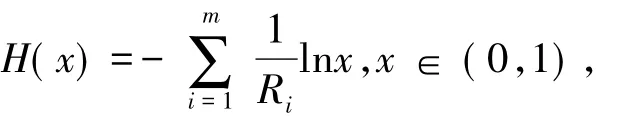
则 H(x)=u－u0有唯一解x1，x1∈(α，1)，于是分配到第i个险种的资本是出储备资金u0的目的是将它追加入第i(i=1，2，…，m)个险种能够使得最终破产的概率不超过α，即

可得分配到第i个险种的资本

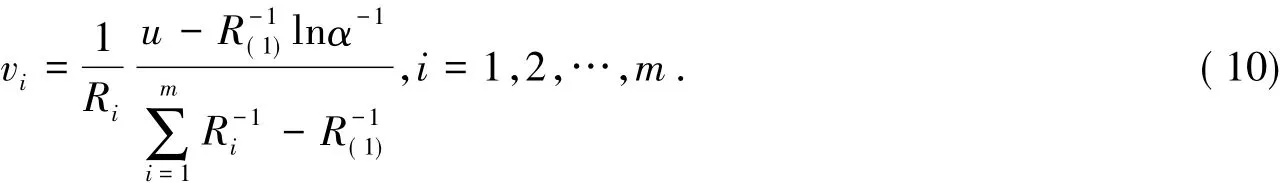
综上，当这m个险种中首个即将破产时，就将储备资金u0注入该险种可使最终破产的概率不超过α，但对于来临的第二个破产险种，就无能为力了．

以上考虑了m个险种的每个险种独立经营自负盈亏时较优的分配初始资本u的几个策略方案．如果这m个险种的盈余可以互补，把m个险种作为一个整体来考虑，我们建立了多险种破产模型(4)，下面讨论保险公司准备多少初始资本u，可使模型(4)最终破产的概率不超过α．

由定理2可知求解不等式e－Ru≤α比独立经营自负盈亏时的初始资本少的多了．

参考文献

［1］ Cheng Shixue，Wu Bao．The survival probability infinite time period in fully discrete risk model［J］．Applied Mathematics，A Journal of Chinese Universities:B，1999，14(1):67－74．

［2］ Cheng Shixue，H．U．Gerber，E．S．W．Shiu．Discounted probabilities and ruin theory in the compound binomial model［J］．Insurance:Mathematics and Economics，2000，26(2):239－250．

［3］ P．Embrechts，T．Mikosch．Modelling extremal events:for insurance and finance［M］．New York:Springer－Verlag，1997:183－199．

［4］ J．Paulsen．Ruin theory with compounding assets－a survey［J］．Insurance:Mathematics and Economics，1998，22(1):3－16．

［5］ H．U．Gerber，E．S．W．Shiu．Pricing perpetual options for jump processes［J］．North American Actuarial Journal，1998，2(3):101－107．

［6］ H．U．Gerber，E．S．W．Shiu．From ruin theory to pricing reset guarantees and perpetual put options［J］．Insurance:Mathematics and Economics，1999，24(1/2):3－14．

［7］ 曲中宪，徐中海．随机投保费下多险种破产模型的研究［J］．东北师范大学学报:自然科学版，2010，42(1):18－21．

［8］ 曲中宪，武文华．随机保费的多险种破产模型［J］．东北电力大学学报，2009，29(2):59－63．

［9］ 成世学．破产论研究综述［J］．数学进展，2002，31(5):403－422．

［10］曲中宪，武文华，徐中海．L－C经典破产模型的推广及应用［J］．北华大学学报:自然科学版，2009，10(4):300－303．