考虑土-结构相互作用的输电塔风振系数计算
刘春城,龙祖良,查传明,王重阳,葛旋宇
(1.东北电力大学建筑工程学院,吉林 吉林 132012;2.中国电建集团贵州电力设计研究院有限公司,贵州 贵阳550081;3.国网新疆电力公司经济技术研究院,新疆乌鲁木齐830013)
随着我国经济的高速发展,输电塔建设风起云涌,作为高柔结构,风荷载对其影响越来越显著[3].时常造成倒塔事故,严重影响人民的生活[4].因此,加强对输电线路风振系数计算的研究,具有十分重要的意义.
针对输电塔结构风振系数计算的研究,邓洪洲、吴昀等[5]结合崖门大跨越实例,统计计算了现行规范的风振系数取值.赵峰、孙威[6]结合汉江大跨越,分别采用规范、三维建模分析和二维简化分析三种方法计算其风振系数.徐明鸣、何洪波[7]根据风速时程模拟和结构随机振动理论,提出输电塔结构风振系数计算的技术思路和实现方法.以上研究存在这一问题:没有运用新荷载规范同时考虑土-结构相互作用对其影响.
邓洪洲、段成荫[8]总结了新荷载规范对顺风向风振系数的修改要点,最后提出了与新荷载规范形式相协调的高耸结构风振系数表达式.范玉娟、邓洪洲[9]采用有限元法分析了输电塔的动力特性,对比了由于新荷载规范湍流度的提高对输电塔结构位移响应和加速度响应的影响,并把模拟结果计算出的风振系数和新旧荷载规范计算出的风振系数相对比.李峰、贾国庆[10]通过实例计算和对比分析,发现新规范较大幅度的提高了输电塔结构设计风振系数的取值.以上研究利用了新荷载规范计算风振系数,但没有考虑土-结构相互作用对其影响.
本研究为了更准确分析结构风振系数,通过利用新旧荷载规范分别计算考虑土-结构相互作用和基础固支两种工况的风振系数,对比分析4种组合条件下的风振系数值.希望能为输电塔结构的抗风设计及风振响应分析提供一些建议和帮助.
1 有限元建模方法
结构采用的塔型如图1所示,高度为42.6 m,呼称高30 m,材料属性为:弹性模量E=2.1×1011Pa,泊松比υ=0.3,密度ρ=7850 kg/m3,选用的角钢规格有12种,利用ABAQUS软件建立输电塔有限元模型,角钢单元定义为 beam[11].
单腿单桩,桩长、桩径分别为 10 m、0.6 m,弹性模量 E=3×1010Pa,泊松比 υ=0.3,密度 ρ=2 500 kg/m3,桩本构模型假定为线弹性.本研究选取的土体区域长和宽为50倍桩径,高取2倍桩长.采用的土体参数如表1所示,土体的本构模型采用Mohr-Coulomb,桩土相互作用采用主从接触面法.

表1 场地土体参数
通过ABAQUS软件建模,得到考虑SSI的整体有限元模型和基础固支的输电塔三维模型,考虑SSI的整体有限元模型,如图2所示.
2 动力特性分析
分别对考虑SSI和基础固支工况下有限元模型进行动力特性分析,采用软件中Block Lanczos方式提取输电塔前10阶振型.图3为固支工况下结构的第1阶、2阶、5阶、6阶振型图,由结果可以看出,第1阶、2阶振型分别为横向、纵向侧移变形,第5阶、6阶振型分别为结构横向、纵向二次侧移变形.
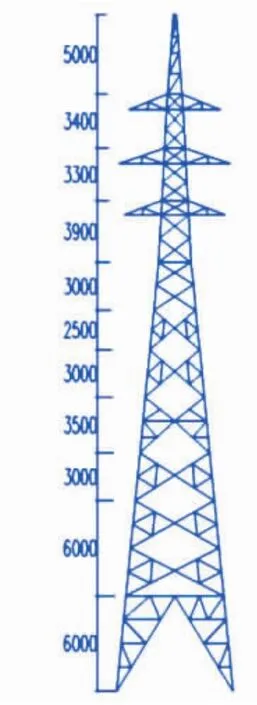
图1 输电塔立面图

图2 考虑SSI的整体有限元模型

图3 固支工况下第1阶、2阶、5阶、6阶振型
图4为I类工况下考虑土-结构相互作用结构的第1阶、2阶、8阶、9阶振型,如图4所示.由图可知,第1阶、2阶振型都为输电塔底部构件扭曲变形,直至第8阶振型,才发生结构一次横向侧移变形,第9阶振型发生结构一次纵向侧移变形,由此得出,考虑土-结构相互作用后,输电塔相应的振型有所滞后.

图4 考虑SSI的第1阶、2阶、8阶、9阶振型
分别提取考虑SSI和基础固支工况下前10阶的自振频率,如表2所示,考虑SSI的结构自振频率比基础固支自振频率有显著的减小;相反,自振周期有显著的增大.

表2 自振频率表
3 风振系数计算
2001年荷载规范中风振系数计算公式采用脉动增大系数和脉动影响系数形式:
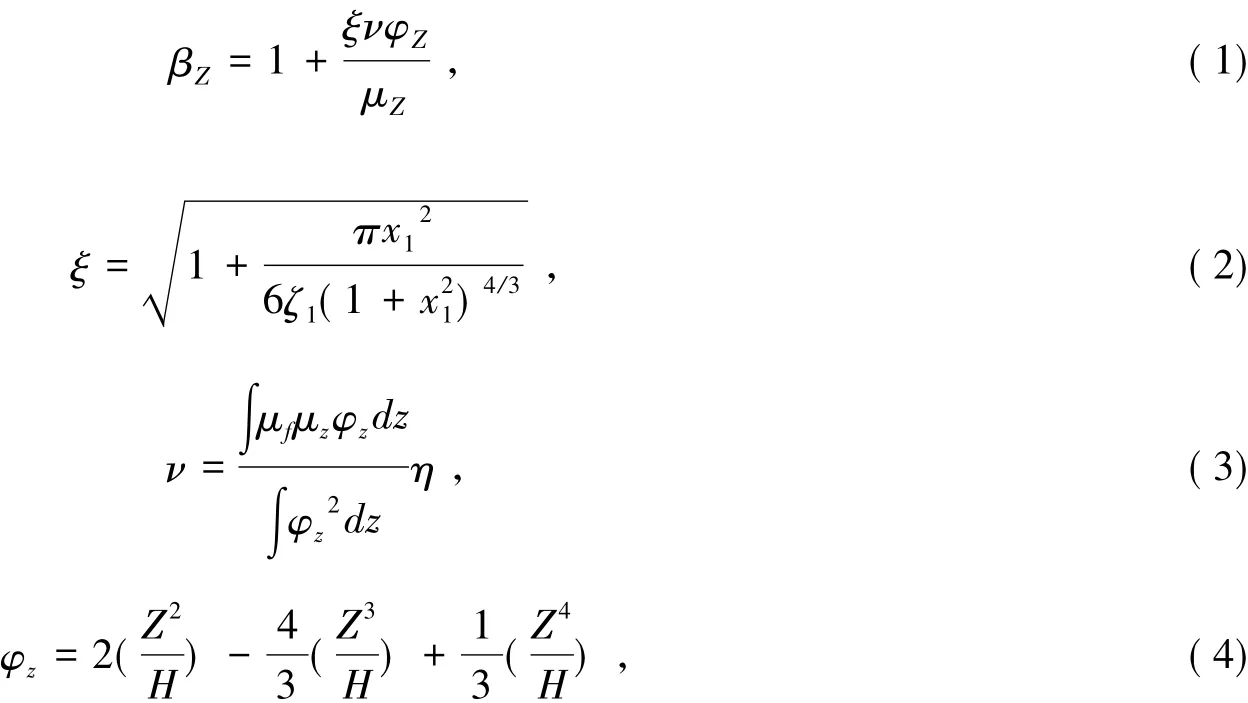
式中:ξ为脉动增大系数;ν为脉动影响系数;φΖ为结构振型系数;μΖ为风压高度变化系数.2012年荷载规范对风振系数计算进行了较大的改动.
2012荷载规范风振系数计算公式采用背景响应和共量响应的表达形式:

式中:g为峰值因子,为常量;Ι10为10 m高度名义湍流强度,为常量;R为脉动风荷载的共振分量因子;ΒΖ为脉动风荷载的背景分量因子.
分别利用新旧荷载规范计算考虑SSI和基础固支工况下输电塔结构上11个点处的风振系数.表3、表4分别为旧、新荷载规范计算得出基础固支和考虑SSI两种工况下塔段的风振系数,考虑SSI后,输电塔结构风振系数有不同程度的增大,最大增幅为8.35%.

表3 旧荷载规范下两种工况的风振系数值

表4 新荷载规范下两种工况的风振系数值
分别利用新旧荷载规范计算出两种工况下输电塔的风振系数,为了对比分析新旧荷载规范,分别把考虑SSI的新旧荷载规范计算出的风振系数进行对比分析,如表5所示.相比旧荷载规范,新荷载规范计算得到的风振系数有显著增大,最大增量达30.87%;把基础固支下新旧荷载规范计算得出的风振系数值对比,如表6所示.新荷载规范得到的风振系数值也有非常显著增大,最大增幅为30.65%.

表5 新旧荷载规范下考虑SSI工况的结构风振系数值对比分析

表6 新旧荷载规范下基础固支工况的结构风振系数对比分析
考虑SSI工况和基础固支工况在新、旧荷载规范下计算得出风振系数值对比,如图5所示,图5中一共有4条曲线,分别代表新荷载规范下考虑SSI工况的风振系数值、新荷载规范下基础固支工况的风振系数值、旧荷载规范下考虑SSI工况的风振系数值、旧荷载规范下基础固支工况的风振系数值.由图5可知,新荷载规范下考虑SSI工况的风振系数值最大,这一组合可以更准确的计算结构的风振系数,为以后输电塔结构抗风设计和风振响应分析提高了适当参考.
4 结 论
(1)相比基础固支工况,考虑土-结构相互作用的输电塔自振周期变大,相应的结构振型有所滞后.
(2)考虑土-结构相互作用后,利用新旧荷载规范计算得出输电塔各塔段的风振系数,两种计算结果都有不同程度增大,最大增幅达8.35%,输电塔结构设计和风振响应分析时应该适当考虑土-结构相互作用对其影响.
(3)在基础固支和考虑SSI工况下,相比旧荷载规范,新荷载规范下结构风振系数值都有非常显著地增大,最大增幅达30.87%,设计时必须严格按照新荷载规范进行.
(4)利用新荷载规范计算考虑SSI的输电塔风振系数值,比其它三种情况所得值大,计算结构的风振系数更准确合理.

图5 4种组合风振系数对比
参考文献
[1] GB50009-2012建筑结构荷载规范[S].北京:中国建筑工业出版社,2013.
[2] GB50009-2001建筑结构荷载规范[S].北京:中国建筑工业出版社,2002.
[3] 肖琦,宋玉,孙海军,等.铁塔与抱杆耦合系统抗风能力研究[J].东北电力大学学报,2016,36(6):91-96.
[4] 白俊峰,鞠彦忠,曾聪.龙卷风作用下空间钢架的受力分析[J].东北电力大学学报,2011,31(5/6):46-51.
[5] 邓洪洲,吴昀,刘万群,等.大跨越输电塔结构风振系数研究[J].特种结构,2006,23(3):66-69.
[6] 赵峰,孙威.100m以上输电塔风振系数的研究[D].武汉:武汉科技大学,2011.
[7] 徐明鸣,何洪波,黄满长.输电塔风振系数模拟计算[J].湖南电力,2011,31(3):8-10.
[8] 范玉娟,邓洪洲.新旧荷载规范对输电塔风振的影响[J].电力建设,2013,34(11):22-26.
[9] 邓洪洲,段成荫.新荷载规范下高耸结构风振系数计算探讨[J].特种结构,2013,30(6):1-6.
[10]李峰,贾国庆.新旧荷载规范中输电塔结构风荷载的计算和对比[J].四川建材,2014,40(1):54-55.
[11] 张恩铭,龚靖,曹帅,等.新型输电杆塔的设计研究[J].东北电力大学学报,2011,31(5/6):60-63.

