低秩矩阵在CT图像重建中的应用*

马海英，宣士斌，b，c，向顺灵

(广西民族大学 a.信息科学与工程学院；b.广西混杂计算与集成电路设计分析重建实验室；c.中国-东盟研究中心，广西 南宁 530006)



低秩矩阵在CT图像重建中的应用*

马海英a，宣士斌a，b，c，向顺灵a

(广西民族大学 a.信息科学与工程学院；b.广西混杂计算与集成电路设计分析重建实验室；c.中国-东盟研究中心，广西 南宁 530006)

CT图像重建是医学影像学的重要研究课题，但由于噪声对医学 CT 图像的影响比较大，为了在不牺牲图像精度和空间分辨率的情况下，重建出噪声含量最低的图像，就要选择合适的去噪方法对图像进行预处理.针对于此，笔者提出一种新的CT图像重建算法，重建过程分成两个步骤：首先用低秩矩阵加权核范数最小化(WNNM)进行图像去噪，再用低秩矩阵分解(LRMD)更新CT图像.实验结果表明，提出的方法具有较强的细节保持能力，低秩矩阵的特性简化计算过程，降低算法复杂度，同时保证了重建图像的去噪效果.

低秩矩阵；核范数；CT图像重建

0 引 言

近年来，CT图像重建的统计学习方法发展迅速，这是由于CT扫描时需要低剂量的X射线辐射的同时要保留高质量的重建图像.然而，统计学方法计算量大、耗时长的特点限制了它的实际应用，为了加速统计方法，许多优化技术被提出，这些算法包括：迭代阈值法(Iterative shrinkage/thresholding algorithm,IST)[1]、两步迭代阈值法(Two step iterative shrinkage/thresholding algorithm,TwIST)[2]、快速迭代阈值法(Fast Iterative shrinkage/thresholding algorithm,FISTA)[3]；分裂 Bregman 方法(Split Bregman algorithm)[4]、Bregman 算子分裂方法(Bregmanized operator splitting，BOS)[5]；低秩矩阵恢复(low-rank matrix recovery，LRMR)技术[6]；Tao[7]等在交替最小化方法的基础上提出了交替方向乘子法(Alternating direction method of multipliers,ADMM)[8]；低秩矩阵分解(low-rank matrix decomposition，LRMD)技术是近几年迅速发展起来的一种高维数据分析工具，并在协同过滤(collaborative filtering)、控制(control)、遥感(remote sensing)、量子态层析成像(quantum state tomography)、机器学习和计算机视觉等领域得到广泛应用.近似低秩矩阵，旨在从它的退化视图中恢复潜在低秩矩阵，它在计算机视觉和机器学习中有较大应用.例如，通过人脸面部图像形成矩阵的低秩特性允许我们重建损坏的脸部[9].网飞公司客户数据矩阵就被认为是一种低秩矩阵，因为客户的选择大部分受一些常规因素的影响[10].通过静态相机捕获的视频片段有一个清晰的低秩特性，基于背景建模和前景抽取[11]可以被统计出来.在自然图像中通过非局部相似块形成矩阵也是低秩特性.由于凸凹优化技术的迅速发展，近年来在近似低秩矩阵中有一系列的研究，同时提出许多重要模型和算法.

目前低秩矩阵技术主要包含矩阵填充(matrix completion,MC)[12]、鲁棒主成分分析(robust principle component analysis,RPCA)[13]和低秩表示(low-mnk representation,LRR)[14]三个方面的内容.该技术的理论基础是矩阵的仿射秩最小化理论，即在给定线性方程组约束下，以矩阵的秩作为测度对目标矩阵进行分析和处理.然而，秩最小化问题在理论上是NP难(Non-deterministic Polynomial Hard,NP Hard)的.类似于压缩感知(compressive sensing,CS)中用l1范数代替l0范数[15]，在拓展了约束等距性(restricted isometry property，RIP)条件后，核范数(矩阵的所有奇异值的和)被用来代替秩函数作为原优化问题的目标函数[16].事实上，压缩感知与秩最小化是密切相关的.当矩阵为对角矩阵时，秩最小化问题就是退化为在矩阵的子空间中找一个最稀疏向量的问题.此时，矩阵的奇异值的和就等同于矩阵的对角元的绝对值之和，即求解核范数最小化问题与l1范数最小化问题是等价的.

由于低秩矩阵分解的凸松弛问题，核范数最小化成为近年来研究的重点.标准核范数最小正则化(NNM)[17]每一个奇异值等同于追求目标函数的凸性问题.然而，这也使其在处理许多实际问题中(如，图像去噪、图像恢复)很大程度上限制了它的性能和灵活性，因为有些奇异值有明显的物理意义，应该区别对待.文中，我们研究了加权核范数最小化(WNNM)问题，此处的奇异值被分配了不同的权重，然后利用图像非局部自相似性将提出的WNNM算法进行图像去噪，实验证明提出的WNNM算法在图像定量测量和视觉感知质量方面明显高于许多先进的去噪算法(如BM3D).

文中，我们提出了基于低秩矩阵加权核范数最小化的去噪模型，并将该模型应用于CT图像去噪，同时将基于低秩矩阵分解应用于CT重建，在重建模型中利用前面提出的图像去噪模型进行图像去噪，建立CT数据重建数学模型，利用傅里叶变换和低秩矩阵的特性简化计算过程，降低算法复杂度.实验表明本文提出的方法具有较好的去噪效果，且为CT重建中的图像去噪步骤提供了坚实的基础，同时具有较强的细节保持能力.

1 相关工作

(1)

我们所要求解的去噪后的图像为px.其中，p代表对动态图像投影，‖·‖F为F范数，‖·‖1为l1范数.

1.1 加权核范数进行图像去噪

核范数最小化(NNM)是一个凸性最优问题.由于许多低秩矩阵能通过NNM方法得到很好的恢复并能高效的解决，因此核范数最小化广泛应用于低秩矩阵最优化问题中，它能通过F范数测量观测数据矩阵Y和潜在数据矩阵X的区别，通过奇异值的软阈值法得到一个分析解.由于相同的软阈值将会应用到所有奇异值中，NNM方法显然不太合理，因为不同的奇异值可能有不同的价值，因此他们需要区别对待.为达到这个目的，我们使用加权核范数来正则化X.下式为加权核范数最小化式化：

(2)

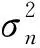
(3)

显然，现在的关键问题是权重向量w的确定.对于自然图像，我们有普遍的先验知识，即pXj的较大奇异值比较小的更重要，因为他们代表Xj主要部分的能量.去噪应用中，奇异值越大，他就应该缩减得越小.因此，权重分配给σi(Xj)，Xj的第i个奇异值应该和σi(Xj)成反比，我们让：

(4)

c>0是常数，n是Yj中相似块的数目，ε=10-16是防止除数为0.

假定噪声能量跨越基底U和V的每个子空间是均匀分布的，然后最初σi(Xj)估计可以写成如下：

(5)

σi(Yj)表示Yj第i个奇异值.通过将以上的程序应用到每个块中然后聚集所有的块，就能重建图像x.实际操作中，我们可以多次运行以上程序以提高去噪质量.整体的去噪算法在算法1中总结出来：

算法1：基于WNNM的图像去噪

输入：噪声图像y

2)for k=1:K do

4)for y(k)中的每个块yjdo

5)找到相似块组Yj

6)评估权重向量w

7)奇异值分解 [U,∑，V]=SVD(Yj)

9)结束

11)结束

2 低秩矩阵分解更新CT图像

在重建模型中利用前面提出的图像去噪模型进行图像去噪，建立CT数据重建数学模型，然后利用低秩矩阵分解的特性将得到的清晰图像运用到锥束CT成像(CBCT)[19]图像重建中.

Cai等人[19]将时间作为一个维度，利用序列CBCT图像中潜在的周期性或重复性等时间上的相关性建模并求解.首先将应用于所有不同投影时刻的图像xi以向量的形式按列依次排成一个矩阵X.矩阵的每一列代表一幅待重建的CBCT图像，矩阵的列数即为投影的次数.该算法的核心思想是矩阵X的秩远小于投影的次数，因此对其进行矩阵的乘法分解X=LR.X中的图像性质分别体现在矩阵L的稀疏性和矩阵R的近似周期性上.首先，矩阵L的列是对矩阵R的秩的约束，无形中对CBCT中所有图像加了一个时间相容性条件.事实上，矩阵L的每一列都是一幅CBCT图像，因此L是可被用于表示矩阵X中的所有图像的一组基.其次，矩阵R的行是矩阵X在基L下的系数，具有一定的周期性或重复性.

可以将CBCT重建看成一个如下最优化问题：

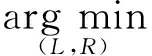
s.t.‖p(LR)-Y‖≤σ2

(6)

其中，p代表对动态图像投影，Y为投影数据，σ为误差控制项.考虑到L和R分别具有稀疏性和潜在的周期性等先验信息，分别采用了在小波紧框架[21]下的稀疏算法d和傅里叶变换f.‖·‖为l1范数，λ为平衡参数.

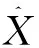
2.1 算法

首先，Cai使用split Bregman[22]方法来解决这个优化问题，首先引入两个辅助变量C和D，那么等式(6)就等价于下式：

s.t.p(LR)=F,C=dL,D=fR

(7)

增广拉格朗日式即：

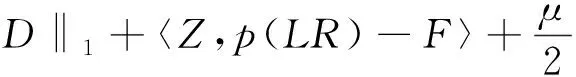
(8)

此处<·,·>表示内积，Z,Z1和Z2表示拉格朗日乘子.合理的固定Z，Z1，Z2，再通过最小化E(C,D,L，R,Z,Z1,Z2)就能找到最优的C，D，L，R.因此，关键是确定Z，Z1，Z2.在增广拉格朗日算法中，我们使用下式进行交替极小化算法：

(9)

这4个子问题通过软阈值法和线性方程求解器(如共轭梯度法)求解.这个算法总结到如下算法中，Γ是软阈值运算符，定义为[Γ(A)]ij=sign([A]ij)·max{‖A‖ij-,0}.

1)通过如下最小化迭代.

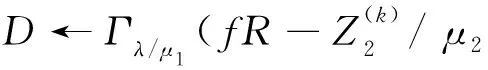
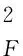
返回.

3)Z(k+1)=Z(k)+(p(L(k+1)R(k+1))-F)

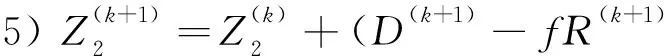
6)k=k+1，返回第1步.

3 图像质量客观评价标准

为了对图像去噪效果进行评价，采用峰值信噪比(PSNR)进行客观评价.令大小为M×N的原图和有噪声图像分别为x和y，PSNR值计算公式如下：

(10)

其中x(i,j)和y(i,j)分别表示图像x和y在位置(i,j)处的幅值.PSNR的值越高表示图像和原图越相似，去噪效果越好.

为了对重建图像效果进行评价，本文采用均方根误差(RMSD)进行评价.

(11)

RMSD值越小表示图像和原图越接近，重建效果越好.

4 实验结果与分析

程序仿真基于VirtualBox centos 6.6-32bit 系统下的Matlab编程环境，在CPU为AMD Athlon2.99 GHz П X2 B24 处理器下，内存为1.75 GB的PC机上运行.视频的分辨率均为480×320.

为了验证文中所提基于低秩矩阵加权核范数最小化的图像去噪算法的有效性，对CT图像进行了仿真测试，并采用峰值信噪比PSNR (Peak Signal Noise Ration)评价标准作为评价图像去噪的标准.

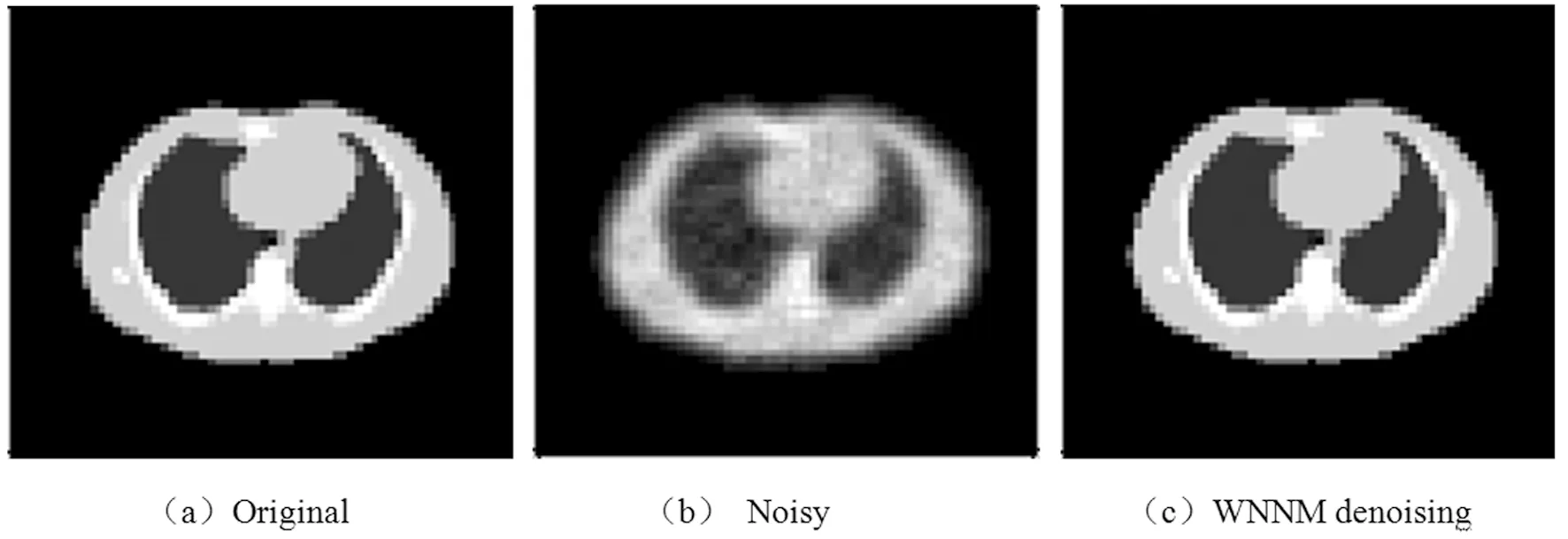
图1 CT图像在WNNM下的去噪效果

为了验证加权核范数最小化(WNNM)去噪效果的优越性，本文对比算法是NNM和BM3D，所用评价标准为PSNR.从表1可以看出，对于CT图像的去噪结果，本文所提算法PSNR值比NNM和BM3D (精确已知噪声标准差的情况)高，因此本文所提去噪算法的去噪结果会比NNM、BM3D好.

为了验证本文提出算法(LRMD-WNNM)的可行性，由于每一个锥束CT(CBCT)图像的重建都是基于相应的瞬时投影.该算法首先进行去噪预处理，然后有效地利用潜在的周期性或重复性等时间上的相关性建模并求解，如图2所示，容易发现本文算法能捕获解剖图的运动状态并恢复得其结构，同时能重构出高分辨率的CT图像.

表1 不同方法的去噪效果(PSNR)

图2 提出算法(LRMD-WNNM)对NCAT体模的重建过程效果图

为了验证本文提出的算法(LRMD-WNNM)相对于Cai提出的简单的LRMD方法更具优越性，分别将这两种方法进行CT重建，由图3可知，提出的算法(LRMD-WNNM)更能有效地去除伪影，具有较好的去噪能力，重建效果更清晰.这主要是由于CT图像在低秩矩阵分解之前进行去噪预处理，因此重建的图像更接近原始图像.

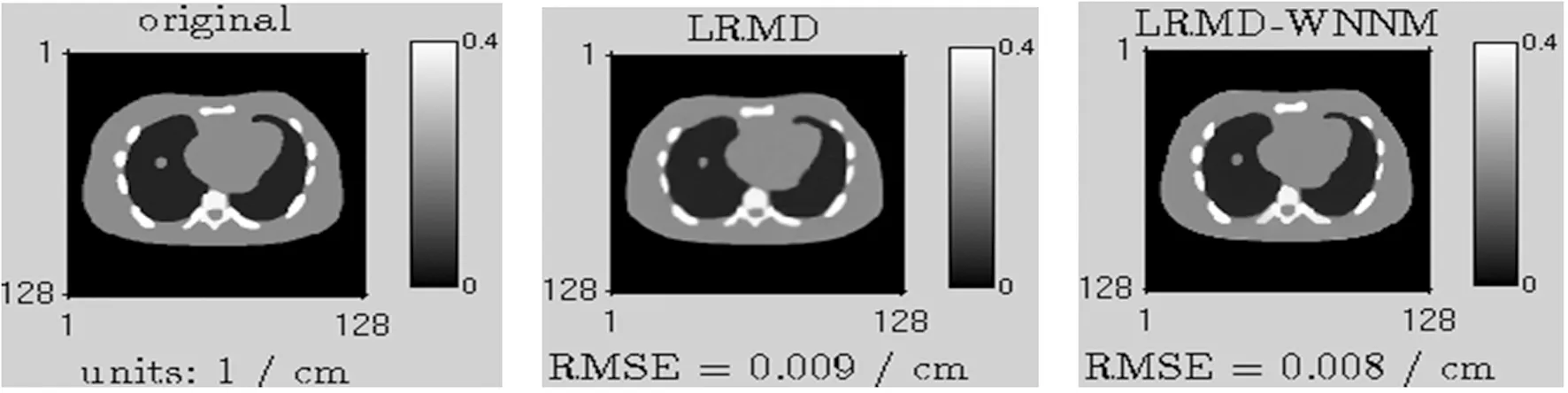
图3 原始图像、简单的低秩矩阵分解(LRMD)和提出的算法(LRMD-WNNM)对NCAT体模的重建效果比较

为了验证提出算法的优越性，实验将三种算法在相同条件下进行的CT图像重建效果比较.图4将滤波反投影法(FBP)、可分二次迭代(SQS)和提出的算法(LRMD-WNNM)进行CT图像重建效果的比较，图5将这三种方法在前10次迭代的RMSD进行了比较.由图可知LRMD-WNNM算法的重建效果优于FBP、SQS算法，这主要是因为LRMD-WNNM算法相对于SQS算法具有更好的稳定性且预先进行了更好地去噪处理，这就使得提出的算法在更新图像的过程中降低了图像伪影，低秩矩阵的特性简化计算过程，降低算法复杂度，提高了算法的收敛速率，同时也降低了RMSD值，具有更优越的重建精度.

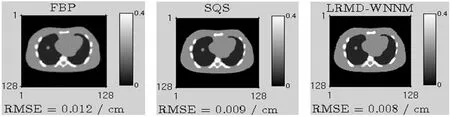
图4 滤波反投影法(FBP)、可分二次代理(SQS)与提出的算法(LRMD-WNNM)对NCAT体模的重建效果比较

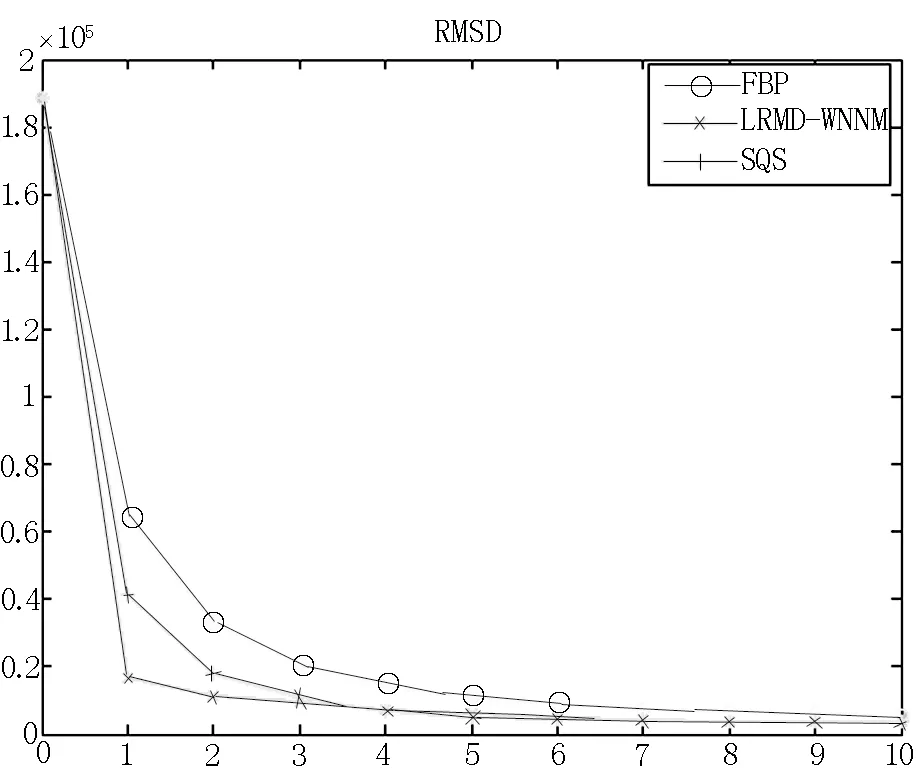
迭代次数

5 结语

本文提出了基于低秩矩阵加权核范数最小化的去噪模型，并将该模型应用于CT图像去噪，同时将基于低秩矩阵分解应用于CT重建，在重建模型中利用前面提出的图像去噪模型进行图像去噪，建立CT数据重建数学模型，利用傅里叶变换和低秩矩阵的特性简化计算过程，降低算法复杂度.实验表明本文提出的方法具有较好的去噪效果，且为CT重建中的图像去噪步骤提供了坚实的基础，同时具有较强的细节保持能力.

尽管这种可行性实验取得了成功，但是对于CBCT的临床应用仍然存在一些实际问题.首先，当把CB几何模型建模成一个立体CBCT图像时，由于涉及极大的数据就会带来一些潜在问题，计算效率也会降低.这些问题能通过一些更有力的计算平台(如计算GPU)得到一定缓解.降低图像质量的另一问题是呼吸模型的奇异性.这种方法在CBCT图像中有效地利用时间相关的周期性，然而它在患者不规则呼吸运动情况下(如咳嗽)时将有所下降，将来可以对那些不规则运动的情形在仿真数据中进行更深远的研究.

[1] Figueiredo M A T,Nowak R D.An EM algorithm for wavelet-based image restoration[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2003,12(8):906-916.

[2] J M Bioucas-Das,M Figueiredo.A new twist:two step iterative shrinkage /thresholding algorithms for image restoration [J].IEEE Transactions on Image Processing,2007,16(12):2992-3004.

[3] A Beck,M Teboulle.Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems [J].IEEE Transactions on Image Processing,2009,18(11):2419-2434.

[4] T Goldstein,S Osher.The split Bregman algorithm for l1 regularized problems [J].SIAM Journal on Imaging Sciences,2009,2(2):323-343.

[5] X Zhang,M Burger,X Bresson,S Osher.Bregmanized nonlocal regularization for deconvo-lution and sparse reconstruction [R].UCLA CAM Report,2009.

[6] Chandrasekaran V,Recht B,Parrilo P A,et al.The Convex Geometry of Linear Inverse Problems[J].Foundations of Computational Mathematics,2012,12(6):805-849.

[7] Y Wang,J Yang,W Yin,Y Zhang.A new alternating minimization algorithm for total varia-tion image reconstruction [J].SIAM Journal on Imaging Science,2008,1(3):248-272.

[8] M Tao,J Yang,B He.Alternating direction algorithms for total variation deconvolution in image reconstruction [R].Available at Optimization-online,2009.

[9] Zheng Y,Liu G,Sugimoto S,et al.Practical low-rank matrix approximation under robust L1-norm[C]// IEEE Conference on Computer Vision and Pattern Recognition，2012:1410-1417.

[10] Salakhutdinov R,Srebro N.Collaborative Filtering in a Non-Uniform World:Learning with the Weighted Trace Norm[J].Advances in Neural Information Processing Systems,2010:2056- 2064.

[11] Mu Y,Dong J,Yuan X,et al.Accelerated low-rank visual recovery by random projection[C]// IEEE Conference on Computer Vision and Pattern Recognition，IEEE Computer Society,2011:2609-2616.

[12]Gamper U,Boesiger P,Kozerke S.Compressed sensing in dynamic MRI[J].Magnetic Resonance in Medicine Official Journal of the Society of Magnetic Resonance in Medicine,2008,59(2):365-373.

[13]Jung H,Sung K,Nayak K S,et al.k-t FOCUSS:a general compressed sensing framework for high resolution dynamic MRI.[J].Magnetic Resonance in Medicine,2009,61(1):103-116.

[14]Ravishankar S,Bresler Y.MR image reconstruction from highly undersampled k-space data by dictionary learning.[J].IEEE Transactions on Medical Imaging,2011,30(5):1028-1041.

[15] Dabov K ,Foi A ,Katkovnik V ,et al.Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2007,16(8):2080-2095.

[16] Akçakaya M,Basha T A,Goddu B,et al.Low-dimensional-structure self-learning and thresholding:Regularization beyond compressed sensing for MRI Reconstruction[J].Magnetic Resonance in Medicine Official Journal of the Society of Magnetic Resonance in Medicine,2011,66(3):756-767.

[17] Lin Z,Liu R,Su Z.Linearized Alternating Direction Method with Adaptive Penalty for Low-Rank Representation[J].Advances in Neural Information Processing Systems,2011:612-620.

[18] Dong W,Shi G,Li X.Nonlocal image restoration with bilateral variance estimation:a low-rank approach.[J].Image Processing IEEE Transactions on,2013,22(2):700-711.

[19] Cai J F,Jia X.Cine cone beam CT reconstruction using low-rank matrix factorization:algorithm and a proof-of-princple study[J].IEEE Transactions on Medical Imaging,2012,33(8):1581 - 1591.

[20] Ron A,Shen Z.Ane systems in L2(IR d ):the analysis of the analysis operator[J].Journal of Functional Analysis,1997,148(2):408-447.

[21] Gao X.Penalized weighted low-rank approximation for robust recovery of recurrent copy number variations[J].Bmc Bioinformatics,2015,16(1):1-14.

[22] The split Bregman method for L1 regularized problems[C]// SIAM J.Imag.Sci，2009.

[责任编辑 苏 琴]

[责任校对 黄招扬]

Low-Rank Matrix Technology for CT Image Reconstruction

MA Hai-yinga,XUAN Shi-bina,b,c,XIANG Shun-linga

(a.CollegeofInformationScienceandEngineering;b.GuangxiKeyLaboratoryofHybridComputationandICDesignAnalysis;c.TheChina-ASEANStudyCenterofGuangxiUniversityforNationalities,GuangxiUniversityforNationalities,Nanning530006,China)

Computed tomography (CT)image reconstruction is an important research subject in field of medical imaging.But as the heavily influence of the noise in medical CT image,We must choose appropriate denoising method for image preproce-ssing to get the lowest noise images,while without sacrificing image precision and spatial resolution.To this problem,this paper proposes a new CT image reconstruction algorithm,the reconstruction process has two steps:first,the low rank weighted nuclear matrix norm minimization(WNNM)which is applied to image denoising.Then a low-rank decomposition of matrix which is used to update CT images.Experimental results show that the proposed method has strong ability to keep the details of the CT images,the characteristics of low-rank matrix to simplify the calculation process,reduce the complexity of the algorithm,and the denoising method has good denoising effect.

low-rank matrix; nuclear norm; CT image reconstruction

2016-04-08.

马海英(1990-)，女，湖南湘潭人，广西民族大学在读硕士，研究方向：图像处理与模式识别；宣士斌(1964-)，男，安徽无为人，博士，广西民族大学教授，硕士生导师，研究方向：图像处理与模式识别.

TP391.4

A

1673-8462(2016)03-0086-07