主元法破解极值点偏移问题

☉安徽省太和县太和中学 岳峻

主元法破解极值点偏移问题

☉安徽省太和县太和中学 岳峻

2016年全国卷Ⅰ的第21题是一道导数应用问题，呈现的形式非常简洁，考查了函数的双零点的问题，也是典型的极值点偏移的问题，是考生实力与潜力的综合演练场.虽然大多学生理解其题意，但对于极值点偏移的本质理解的深度欠佳，面对此类问题大多感到“似懂非懂”或“云里雾里”.

所谓主元法就是在一个多元数学问题中以其中一个为“主元”，将问题化归为该主元的函数、方程或不等式等问题，其本质是函数与方程思想的应用.作为一线的教育教学工作者，笔者尝试用主元法破解函数的极值点偏移问题，理性的对此类进行剖析、探究，旨在为今后的高考命题和高考复习教学提供一点参考.

一、试题再现及解析

（一）题目

（2016年全国卷Ⅰ）已知函数f（x）=（x-2）ex+a（x-1）2有两个零点.

（1）求a的取值范围；

（2）设x1，x2是f（x）的两个零点，证明：x1+x2＜2.

本题第（1）小题含有参数的函数f（x）有两个零点，自然想到研究其单调性，结合零点存在性定理求得a的取值范围是（0，+∞）.第（2）小题是典型的极值点偏移的问题，如何证明呢？

（二）官方解析

（2）不妨设x1＜x2，由（1）知，x1∈（-∞，1），x2∈（1，+∞），2-x2∈（-∞，1），f（x）在（-∞，1）上单调递减，

所以x1+x2＜2等价于f（x1）＞f（2-x2），即f（2-x2）＜0.

由于f（2-x2）=-x2e2-x2 +a（x2-1）2，而f（x2）=（x2-2）ex2+ a（x2-1）2=0，

所以f（2-x2）=-x2e2-x2 -（x2-2）ex2

.

令g（x）=-xe2-x-（x-2）ex，则g′（x）=（x-1）（e2-x-ex），

所以当x＞1时，g′（x）＜0，而g（1）=0，

故当x＞1时，g（x）＜g（1）=0.从而g（x2）=f（2-x2）＜0，故x1+x2＜2.

二、对解析的分析

本问待证是两个变量的不等式，官方解析的变形是x1＜2-x2，借助于函数的特性及其单调性，构造以x2为主元的函数.由于两个变量的地位相同，当然也可调整主元变形为x2＜2-x1，同理构造以x1为主元的函数来处理.此法与官方解析正是极值点偏移问题的处理的通法.

不妨设x1＜x2，由（1）知，x1∈（-∞，1），x2∈（1，+∞），2-x1∈（1，+∞），f（x）在（1，+∞）上单调递增，所以x1+x2＜2等价于0=f（x2）＜f（2-x1），即f（x1）-f（2-x1）＜0.

令u（x）=f（x）-f（2-x）=xe2-x-（2-x）ex（x＜1），则

u′（x）=（x-1）（ex-e2-x）＞0，

所以u（x）＜u（1）=0，即f（x）＜f（2-x）（x＜1），

所以f（x1）=f（x2）＜f（2-x1）.

所以x2＜2-x1，即x1+x2＜2.

三、例谈主元法破解极值点偏移问题

对文献［1］的四道例题，笔者都能运用主元法顺利破解，验证主元法破解极值点偏移问题的可行性.

例1（2014年江苏省南通市二模第20题）设函数f（x）=ex-ax+a，其图像与x轴交于A（x1，0），B（x2，0）两点，且x1＜x2.

（1）求a的取值范围；

单调递减，在（lna，+∞）上单调递增.

因为f′（x）=ex-a单调递增，

所以g（x）在（0，lna）上单调递减，g（x）＞g（lna）=0，得证.

例2（2010年天津理科21题）已知函数f（x）=xe-x（x∈R）.

（1）求函数（fx）的单调区间和极值；（2）（略）；

（3）如果x1≠x2，且（fx1）=（fx2），证明x1+x2＞2.

解：（1）（fx）在（-∞，1）上是增函数，在（1，+∞）上是减函数，（fx）=（f1）=极小值

只需证明f（x2）=f（x1）＞f（2lna-x1）即可.

（3）证明：f′（x）=e-（x1-x），f（x1）=（fx2），亦即= x，且x1＜1＜x2，

欲证明x1+x2＞2，即x2＞2-x1，只需证f（x2）-f（2-x1）＜0，即f（x1）-f（2-x1）＜0.

令g（x）=f（x）-f（2-x）（x＜1），则g（x）=xe-x-（2-x）ex-2，

因为g′（x）=（1-x）（e-x-ex-2）＞0，

所以g（x）在（-∞，1）上单调递增，

故g（x）＜g（1）=0，得证.

例3（2011年辽宁理科21题）已知函数f（x）=lnxax2+（2-a）x.

（1）讨论f（x）的单调性；

（3）若函数y=（fx）的图像与x轴交于A，B两点，线段AB中点的横坐标为x0，证明：f（′x）0＜0.

解：（1）若a≤0，（fx）在（0，+∞）上单调递增；若a＞0，）上单调递增，在）上单调递减；（3）由（1）可得a＞0，f′（x）=-2ax+2-a在（0，+∞）上单调递减，

（2）（略）不妨设A（x，0），B（x，0），0＜x＜x，则0＜x＜＜x，

121212欲证明f′（x）＜0，即f′（x）＜f′），只需证明x=

000

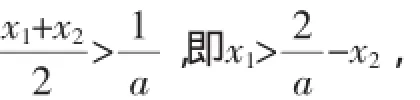
（1）求f（x）的单调区间；

（2）证明：当f（x1）=f（x2）（x1≠x2）时，x1+x2＜0.

解：（1）f（x）在（-∞，0）上单调递增，在（0，+∞）上单调递减.

（2）由（1）知，当x＜1时，f（x）＞0.

不妨设x1＜x2，因为f（x1）=f（x2），即

则x1＜0＜x2＜1，

要证明x1+x2＜0，即x1＜-x2＜0，

只需证明f（x1）＜f（-x2），即f（x2）＜f（-x2）.

而f（x2）＜f（-x2）等价于（1-x2）e2x2-1-x2＜0，

令g（x）=（1-x）e2x-1-x（x＞0），则g'（x）=（1-2x）e2x-1，

令h（x）=（1-2x）e2x-1，则h′（x）=-4xe2x＜0，

所以h（x）单调递减，h（x）＜h（0）=0，即g′（x）＜0，所以g（x）单调递减，

所以g（x）＜g（0）=0，得证.

对文献［3］的例1，朱老师提供了3种方法，笔者也可运用主元法顺利破解，请看以下解析，岂不更为简捷？

例5函数（fx）=x4-x3与直线）交于A（x1，a），B（x2，a），证明：x1+x2＜2.

若0＜x1＜1，1＜x2＜，要证明x1+x2＜2，即0＜x1＜2-x2＜1，

只需证明（fx1）＞（f2-x2），即（fx）2＞（f2-x2）.

令g（x）=（fx）-（f2-x）（x＞1），

所以g（x）＞g（1）=0，得证.

1212

四、通法提炼

一般地，主元法破解极值点偏移问题思路是：

第一步：根据f（x1）=f（x2）（x1≠x2）建立等量关系，并结合f（x）的单调性，确定x1，x2的取值范围；

第二步：不妨设x1＜x2，将待证不等式进行变形，进而结合原函数或导函数的单调性等价转化.如例1、例3中的待证是导函数的值的不等式，因此应用导函数的单调性等价转化，例2、例4中的待证是应用原函数的单调性等价转化；

第三步：构造关于x1（或x2）的一元函数T（x）=f（xi）-f（2a-xi）（i=1，2），应用导数研究其单调性，并借助于单调性，达到待证不等式的证明.

五、通性通法的感悟

极值点偏移问题在高考中几乎年年可见，深受高考命题专家的青睐，年年岁岁意相似，岁岁年年题不同，属于高考高频题型.对于此类问题的研究，多位方家已经作了探讨.

文［1］从高等数学的视角阐述了问题的背景，指明并提炼出极值点偏移问题的解题策略：若（fx）的极值点为x0，则根据对称性构造一元差函数F（x）=（fx0+x）-（fx0-x），巧借F（x）的单调性以及F（0）=0，借助于（fx）1=（fx2）=［fx0-（x0-x2）］与f［x0+（x0-x）2］=（f2x0-x）2，比较x2与2x0-x1的大小，即比较x与的大小.有了这种解题策略，我们师0生就克服了解题的盲目性，细细咀嚼不得不为其绝妙的想法喝彩，但是，此解法并不利于学生思维的提升，比较突兀，有“模式化”的曲高和寡之嫌疑，显然不是自然的想法，“想说爱你不容易.”教师的自然想法却让学生屡屡想不到、想不通、学不会，加重其自卑感；顺应学生的思维，才能对接学生的认知，贴近学生“最近发展区”，化用于无痕，活用于无间，妙用于无限，神用于无形，走有限之路，饮不竭之泉.

文［2］结合文［1］的四个例题验证了转化为对数平均的求解的可行性，提炼出极值点偏移问题的又一解题策略：根据f（x1）=f（x2）建立等式，通过消参、恒等变形转化为对数平均，捆绑构造函数，利用对数平均不等式链求解.这种解题策略，师生都感到运算量繁杂，有一定的技巧要求，而且对数平均数的不等式链也有超纲的嫌疑，在解答过程中存在能否直接运用的疑问［4］，“想你，但，我不会爱你！”

其实，解决极值点偏移问题的上两种方法，实质上都是把双变量的等式或不等式转化为一元变量问题求解，途径都是构造一元函数，因此，主元法才是破解极值点偏移问题的通法，亲切自然，美感灵气.这一点也可以从官方答案得到印证.对于官方提供的参考答案，是命题专家经过反复考量的，承载着新课程改革的理念和导向，渗透着创新精神和实践能力的培养，体现着高考改革的发展趋向，同时也蕴含着命题者解题的思维历程，蕴含着其问题的本质.我们多一份敬畏，将参考答案激活，用“冰冷的美丽”促进学生“火热的思考”，多一份收获.

六、质疑

文［1］中提到“利用极值点对折，构造一元差函数F（x）=f（x0+x）-f（x0-x）的解题策略”是极值点偏移问题的本质之所在.文［2］中又称“极值点偏移问题的另一本质回归—对数平均.”到底哪一种方法是极值点偏移问题的本质？极值点偏移问题的本质可否有多种？某一种解题策略是否为此类问题的本质又如何判断？有待于方家探讨.

1.邢友宝.极值点偏移问题的处理策略［J］.中学数学教学参考（上），2014（7）.

2.赖淑明.极值点偏移问题的另一本质回归［J］.中学数学教学参考（上），2015（4）.

3.朱红岩.极值点偏移的判定方法和运用策略［J］.中学数学教学参考（上），2016（3）.

4.岳峻，童永奇.对数平均数不等式链的几何证明与变式探究［J］.数学通讯（教师版），2016（11）.Z