双站无源定位精度与布站仿真分析

任时兴，孙晓峰

(1.中国电子科技集团公司第36研究所，嘉兴 314033； 2.海军702厂，上海 200434)



双站无源定位精度与布站仿真分析

任时兴1，孙晓峰2

(1.中国电子科技集团公司第36研究所，嘉兴 314033； 2.海军702厂，上海 200434)

根据定位平台与目标的几何关系、测向测时误差、定位精度要求等因素，对基于圆概率误差、定位模糊区和相对误差等不同指标的双站无源定位精度进行仿真，并分析不同态势下定位平台的布站形式，对双多站无源定位具有现实意义。

无源定位；定位精度；布站

0 引 言

无源定位已广泛应用于海空平台远距离目标定位，基于到达方位角度以及到达时间差的定位方法是无源定位中常用的2种方法。由于无源定位平台与目标的几何态势不同,最优交会角的定位精度标准各异[1-4]，导致了无源定位交会角和布站方式上不同结论的出现。文献[1]～[3]分别从圆概率误差(CEP)和模糊定位面积的角度对测向交叉定位的最优夹角进行了研究，文献[4]在相对误差条件指标下讨论了传感器测角精度、平台间距和目标三者构成的三角形形状之间的关系，文献[5]讨论了二维平面时差定位中最佳传感器分布。本文在圆概率、定位模糊区和相对误差等定位准则的基础上，通过理论和仿真计算，对双站多站测向测时无源定位的精度、布站优缺点进行分析，为提高双多站无源定位精度提供参考。

1 无源定位精度

无源定位系统中通常采用3种指标来衡量目标定位精度。一种是圆概率误差，它是指目标落入给定区域内概率为50%的误差分布圆半径，此时的定位误差等概率轮廓线为一个椭圆；其次是定位模糊区，通过测向交叉定位系统中定位模糊区面积达到最小值的必要条件来推导传感器平台最优配置角；第3种是相对误差标准，分析雷达测角精度、基线测量精度一定的情况下定位误差与传感器布站的关系，给出定位误差与传感器布站之间的关系。

如图1所示，设有一辐射源位于xy平面的E点(xe,ye)。在装载侦察设备的定位平台位A(x1,y1)和B(x2,y2)上对辐射源测向，测得的方位角分别为θ1和θ2(以方位基线为基准)。2个位置线的夹角为β(无源定位交会角)，辐射源到方位基线的距离为D，2个侦察站之间距离为L。根据已知的点A和B坐标(x1,y1)、(x2,y2)和方位角θ1、θ2便可以确定辐射源E点的坐标(xe,ye)。由于测向总是存在误差，所以会产生对目标的定位误差。计算目标的位置误差为：

(1)

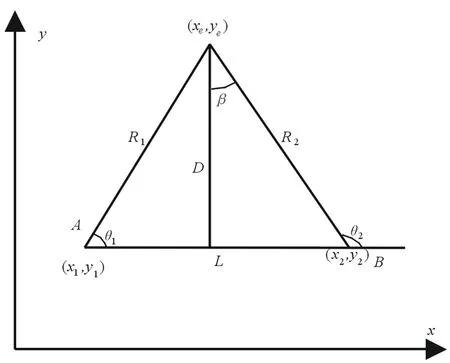
图1 双站无源定位图

1.1 圆概率误差

图1中，θ1，θ2的测量误差分别为Δθ1，Δθ2，当测量误差较小时，可用微分代替增量的办法对定位误差进行分析，可得圆概率误差：

(2)

若把目标到基线的距离D看作是常量，则可求得协方差rxx、ryy的显式表达式为：

(3)

(4)

(5)

则将式(3)、(4)代入到式(2)中整理化简，可求得圆概率误差r0.5为：

(6)

式中:σθ1和σθ2以弧度为单位。

由此可看出，圆概率误差r0.5与基线长度L、传感器测角误差的方差σθ1和σθ2、2个无源观测站所测得的方位角θ1，θ2以及交会角β有关。

经推导得出[1-2]，当θ1=±35°，θ2=±145°时，圆概率误差最小，定位精度最高。此时，2个无源观测站和目标呈等腰三角形分布，交会角的绝对值|β|=110°。

1.2 定位模糊区CEP

由于内部噪声的影响，在方向角测量过程中出现的随机测向误差会使不同传感器2条测向线的交点围绕着真实点E随机分布，在辐射源附近形成一个定位模糊区，可用四边形来近似表示，如图2所示。

图2 定位模糊区

由于2个无源观测平台的测角误差很小，求得阴影部分的面积为:

(7)

1.3 相对误差

双站无源定位精度不仅与侦察雷达的测向精度、定位海空平台之间距离测量精度有关，还与目标和定位平台构成的三角形的形状有关。因为传感器测向、定位海空平台之间距离测量都有误差，而目标距离通过解三角形得到，根据误差传递原理，测向、定位平台之间距离测量误差肯定会传递到目标距离测量中，当传感器测向、定位平台之间距离测量误差一定时，定位误差的大小与三角形的形状有关。根据上述时间序列数据解三角形，即可求出任意时刻的目标到定位平台的距离R1，R2:

(8)

(9)

为分析定位误差的大小，在式(8)中将R1分别对R3，θ1，θ2求偏导，则：

(10)

(11)

(12)

根据误差传递公式，得到侦察雷达定位的相对误差表达式：

(13)

1.4 时差定位CEP

对于基线时差定位体制，与测向定位同样的配置下，二维平面定位的误差方差[5]可表示为：

(14)

定位误差的圆概率误差表示为：

(15)

当各副站传感器均匀分布在以主无源站为圆心的圆上时，可得到目标位置坐标的最小Cramer-Rao下界，此时的传感器分布为二维平面时差定位中最佳传感器分布[5]。

2 仿真分析

假设无源传感器的探测范围：x轴方向为±100 km，y轴方向为±100 km；2个测向站位置分别为(-50 km,0 km)和(50 km,0 km)，测向误差的标准差均为1.5°；3个时差站位置分别为(0 km,0 km)，(30 km,0 km)，(60 km,0 km)，时差测量精度30 ns。

图3为基于圆概率误差等值线图，图4为无源站与目标构成三角关系中无源定位圆概率误差极小值。2个或多个无源站实施测向定位时，圆概率误差取决于被动传感器的测向均方误差。理论上，该方法最优交会角为110°，且有确定、可知的全局最小定位精度值。由图4可看出圆概率误差极小值曲线有规律，成对称分布，根据文献[1]和数值仿真结果，验证圆概率误差为指标时，无源定位最优交汇角为β=110°，无源站目标角为θ1=θ2=35°。图5为测向交叉定位的模糊区等值曲线，经理论计算，该方法无全局最小值，其较优交会角通常为60°左右。图6为无源站与目标构成三角关系中无源定位模糊四边形面积极小值曲线。曲线呈锯齿状，变化无规律，θ1、θ2中一个为接近0°的小锐角，另一个为接近90°的角度。模糊区面积无全局最小值，离主无源站越接近其相对误差越小。这种态势的发生，对无源定位的战术使用无实际意义。

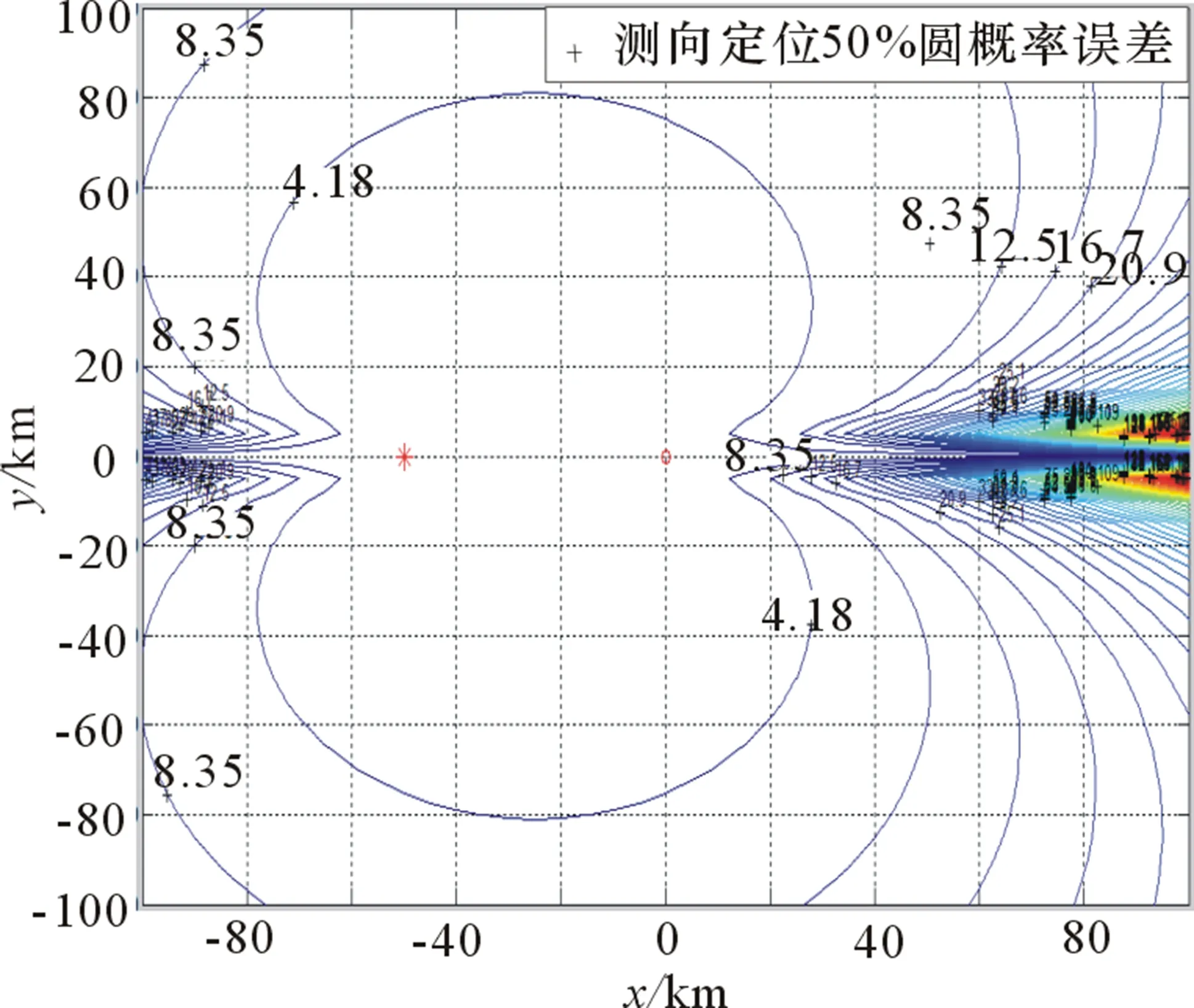
图3 测向定位的圆概率误差

图4 圆概率误差最小值变化

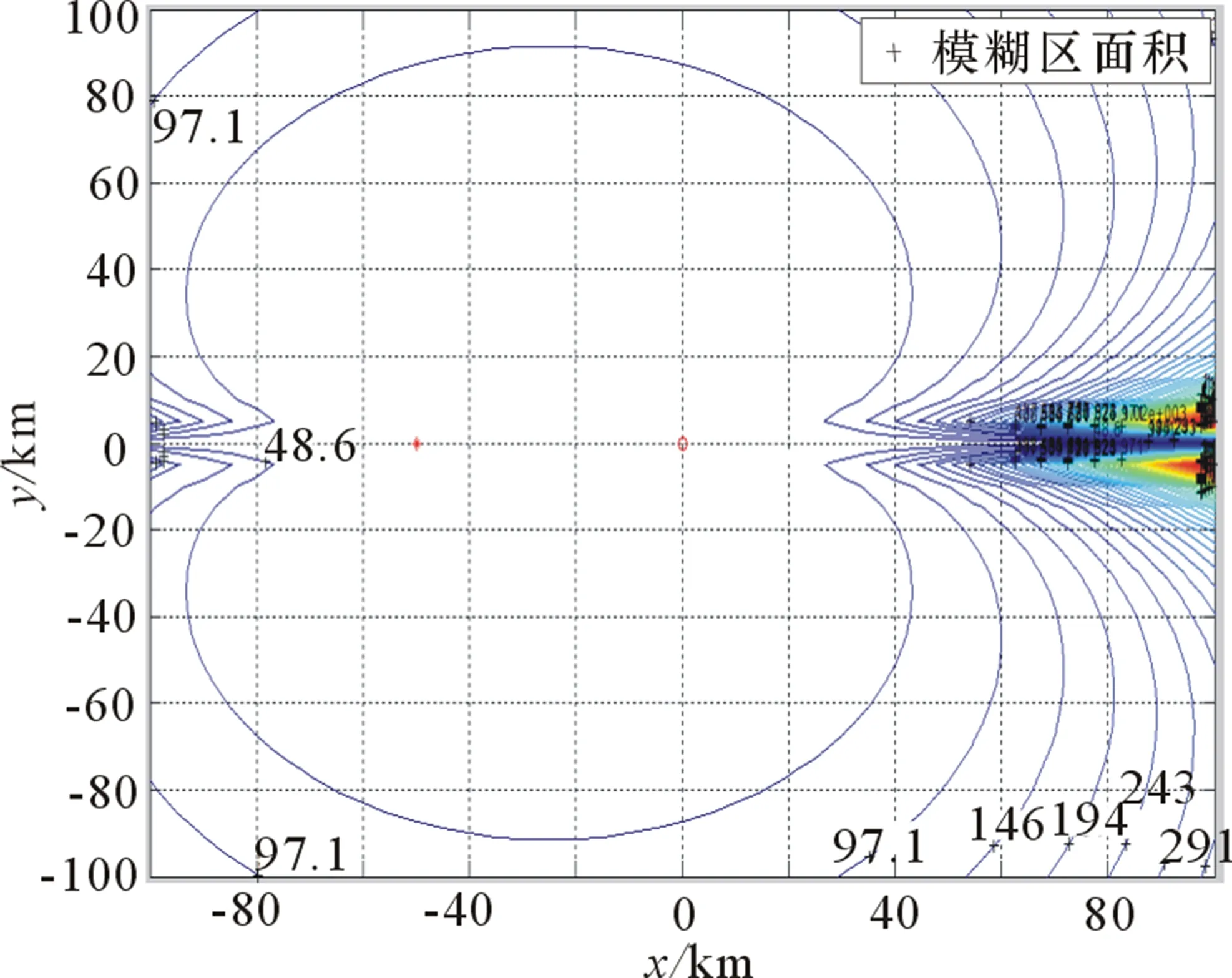
图5 测向定位的模糊区面积

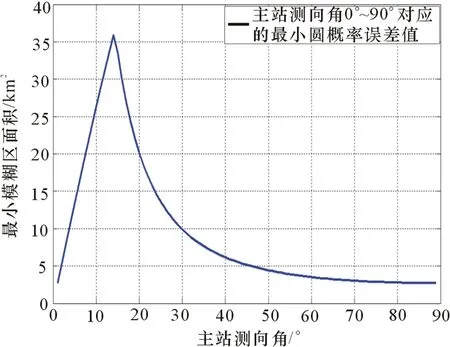
图6 模糊四边形面积最小值变化

图7为相对误差等值曲线，通常用于确定目标相对于主要攻击平台的相对误差(ΔR1/R1)，而与另一平台距离无关联，未充分利用编组平台全部信息。采用该方法计算定位精度时，ΔR1/R1的大小与目标的远近(R1的大小)无关。当θ1较小(接近0°)或较大(接近180°)时，无源测向定位相对误差很大；在基线中垂线附近时，无源定位误差相对较小；但距离无源站基线距离越近，误差越小。从相对误差等值曲线图看，相对误差无全局最小值，离主无源站越接近其相对误差越小，情形与模糊区定位误差相类似。图8为时差定位精度等值曲线，在相同定位精度曲线上，基线中垂线上的目标距离无源站最远，此时无源站与目标构成等腰三角形，与文献[5]的结论一致。

图7 测向定位的相对误差

图8 时差定位误差

3 结束语

圆概率误差取决于被动传感器的测向均方误差，该方法且有确定、可知的全局最小定位精度值，最优交会角为110°；测向交叉定位的模糊区方法无全局最小值，其较优交会角通常为60°左右，离主无源站越接近其误差越小；相对误差方法较优交会角为90°，无全局最小值，离主无源站越接近其相对误差越小；时差定位方式，无源站与目标构成等腰三角形时，定位误差相对较小。

[1] 修建娟,何友.测向交叉定位系统中的交会角研究[J].宇航学报,2005(3):282-286.

[2] 白晶,王国宏.测向交叉定位系统中的最优交会角研究[J].航空学报,2009(2):298-304.

[3] 王本才.多站无源定位最佳配置分析[J].中国科学(信息科学),2009(2):1251-1267.

[4] 李兴民,李国君,李健.双站交叉定位雷达布站方法研究[J].雷达科学与技术,2011(5):405-408.

[5] 易云清,徐汉林,王化.时差定位的传感器位置分布研究[J].计算机应用,2009(12):58-65.

Analysis of Dual-station Passive Location Precision and Station Distribution Simulation

REN Shi-xing1，SUN Xiao-feng2

(1.The 36th Research Institute of China Electronic Science & Technology Group,Jiaxing 314033，China;2.Factory 702,Shanghai 200434，China)

According to the factors such as the geometrical relationship between location platform and target,direction finding (DF)/time finding error,location precision request,etc.,this paper simulates the precision of dual-station passive location based on the indexes such as circular probable error,ambiguous location area and relative error,etc.,and analyzes the station distribution type of location platforms under different situation,which is valuable to analyze the double/multiple stations passive location.

passive location;location precision;station distribution

2016-01-19

TN971

A

CN32-1413(2016)03-0015-04

10.16426/j.cnki.jcdzdk.2016.03.004