干涉仪测向技术研究
赵小华,梁广真
(中国船舶重工集团公司第723研究所,扬州 225001)
干涉仪测向技术研究
赵小华,梁广真
(中国船舶重工集团公司第723研究所,扬州 225001)
干涉仪测向具有测向精度高、灵敏度高、观测频带宽等特点,因而在电子对抗、雷达等领域中广泛应用。但是相位干涉仪的弱点是测角的线性范围小,当角度超过其不模糊视角时容易产生相位模糊。针对相位模糊问题,提出了参差基线法、虚拟基线法2种解模糊方法,并通过仿真实验比较其解模糊能力。
干涉仪测向;解模糊;参差基线法;虚拟基线法
0 引 言
现代战争是高科技的战争,电子对抗对战争胜负有着至关重要的作用,其中对敌方雷达的情报侦察更是电子对抗的关键。在现代空间高科技技术支撑下,电子侦察卫星可以在不受区域国界限制的情况下,对针对地区的辐射源进行侦察定位,从而掌握敌方雷达的技术参数、指标和分布情况[1]。
电子侦收是通过电子侦察设备取得敌方军事情报,以便我军进行电子进攻和电子摧毁。电子侦收是对敌方军事电子设备辐射的电磁信号进行截获、检测、分析、识别、定位,以便确定敌方军事电子设备及相关平台对己方的威胁程度,为己方指挥决策和电子战装备设计提供情报支援[2]。
相位干涉仪的测向精度比较高,广泛应用于电子侦察领域。相位干涉仪只能在[-π,π]范围单值测量相位差,但单基线相位干涉仪存在测向精度和最大不模糊角度之间的矛盾。传统的解模糊方法是利用长短基线结合的办法,要求短基线长度小于λmin/2,但对于高频信号,λmin会非常小,这将会导致低频率信号在各个阵元之间的耦合,造成波达角测向精度和分辨率的降低[3]。更为严重的是:干涉仪阵元本身的物理尺寸由信号的最长波长决定,这使得在最小半波长的空间内无法安装2个阵元,即传统方法很难在工程上实现。
为了解决干涉仪测向中存在的相位模糊问题,提出了参差基线法、虚拟基线法这2种解模糊方法,分析其优缺点并通过仿真实验比较其解模糊的能力。
1 单基线干涉仪测向
经典的干涉仪测向系统一般由4个部分组成:测向天线阵、多波道接收机、测向处理单元和遥控设备,如图1所示。

图1 干涉仪测向系统模型
单基线指的是测向系统只由1组测向基础构成。如图2 所示的最简单的一维(只能测量入射俯仰角)单基线相位干涉仪,它只有1组且只有1条基线。D为阵元之间的间距,θ是信号入射的方位角,λ是载波的波长[4]。
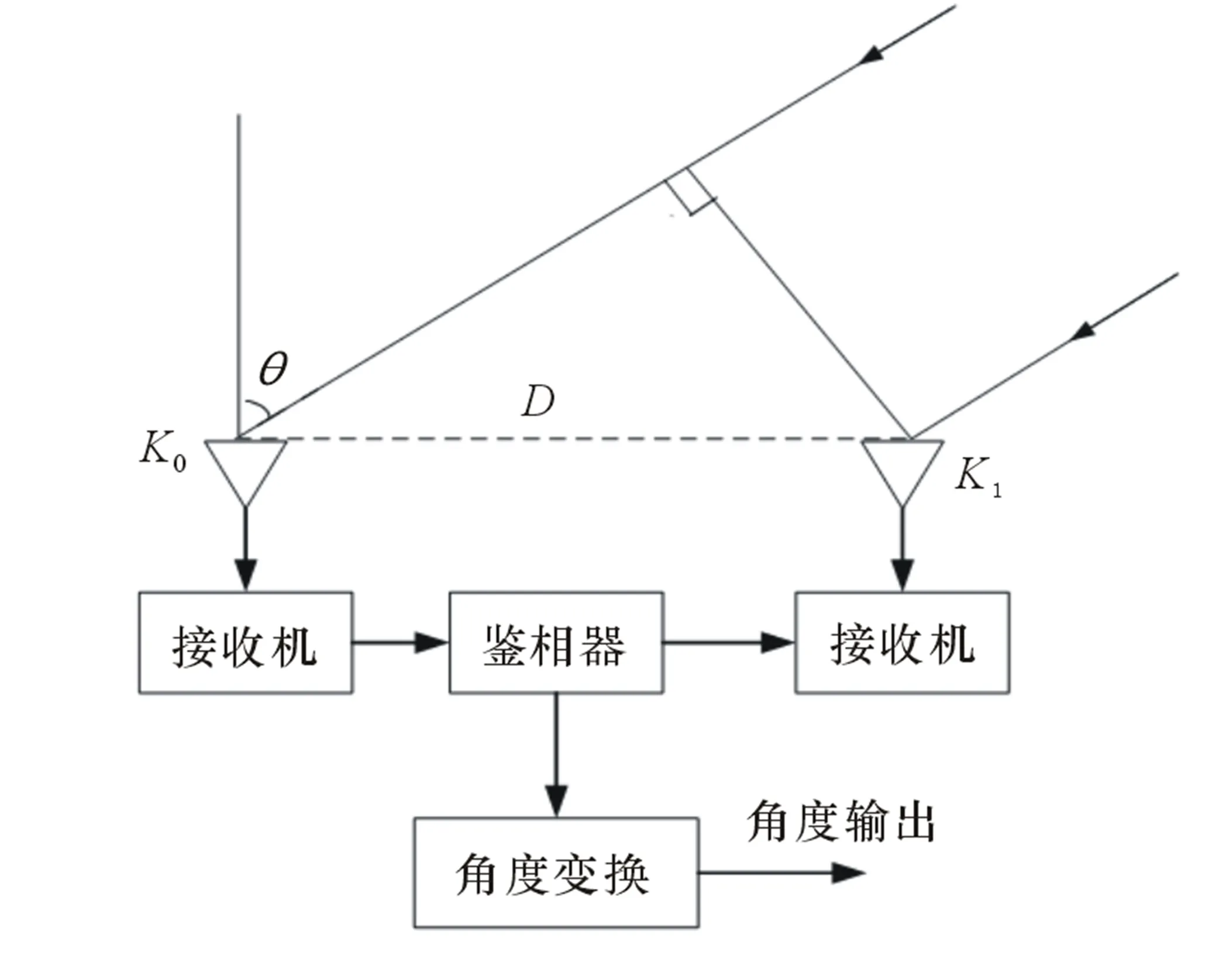
图2 单基线一维相位干涉仪
则可得两阵元接收到信号的空间相位差为:
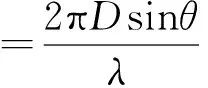
(1)
由于鉴相器无模糊的相位检测范围为[-π,+π],可以得到单基线干涉仪测向的最大不模糊测角范围为 [-θmax,θmax],根据式(1)可获得最大相位差为π时的信号到达角θmax为:
(2)
可以发现,当一维相位干涉仪进行测向时,如果同一信号的入射角分别来自θ方向和π-θ方向时,这2个方向得到的相位差一样,而且都为2πDsinθ/λ,即存在一个模糊问题,因此考虑采用参差基线法和虚拟基线法解模糊。
2 参差基线法解模糊
当入射信号频率波段比较高时,它所对应的波长就会很小。鉴于此就会产生几个问题:一是为了解模糊,在长短基线法中往往需要最小基线长度小于半波长,而这在实际工程中很难实现,所以该方法不适用;二是由于基线长度较短,天线阵元之间会产生耦合现象,影响相邻天线的相位差,最后影响测量结果,所以基线长度也不能过短。因此,结合上述情况,在实际宽频带测向系统中,可以用参差基线法来解模糊,其原理主要是余数定理。
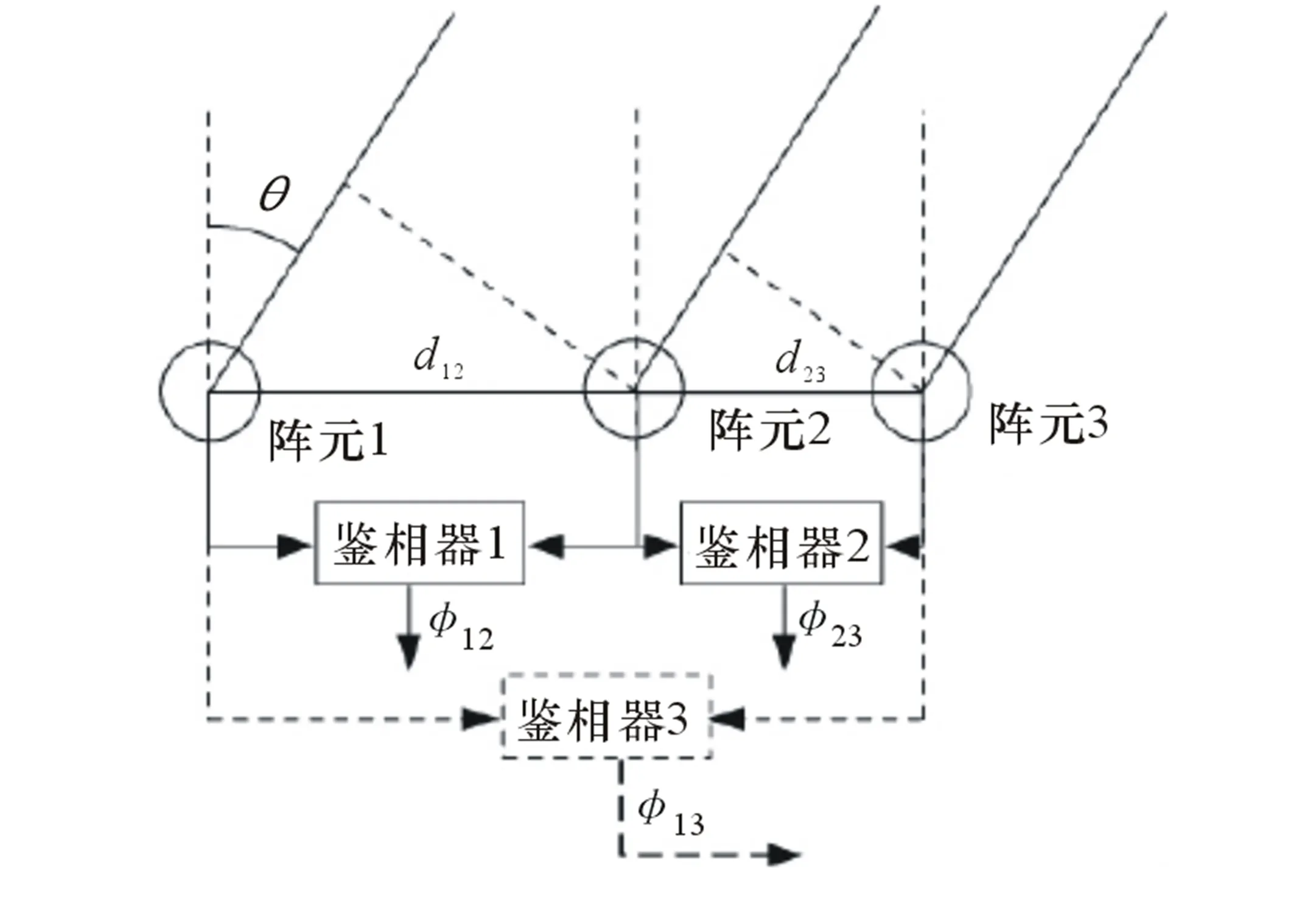
图3 双基线干涉仪原理图
这里以双基线为例,设d12=m1x,d23=m2x(其中,m1和m2必须互为质数,x<λ/2)。同样,φ1,φ2分别为短基线和长基线对应的有模糊相位差,来求取两基线对应的无模糊相位差φ1和φ2。根据干涉仪测向原理有:
(3)
(a) 当θ>0时,把φ1,φ2化到[0,2π)的区间范围,这时N1,N2≥0,将式(3)进行变形得:
(4)
(b) 当θ<0时,把φ1,φ2化到[-2π,0)的区间范围,这时N1,N2≤0,将式(4)中的等式2边同时乘以(-1)得:
(5)
(c) 采用最小二乘法确定入射角。
然而在实际工程中,采用上述方法仍然存在一个问题,即θ究竟是大于0还是小于0,这将决定我们是采用方法(a)还是方法(b)解模糊,若是方法的选择会影响最后的结果,那么就需要判定来波方向。但是经过大量的仿真实验可以发现:若是x的值小于半波长,方法(a)和方法(b)解模糊的结果只有一个有效结果,另一种方法无解,因为sinθ的值不在[-1,1]范围内。
余数定理解模糊随着技术的进步而越来越简单,但是它也有一个缺点,如果因为噪声影响了其中一个余数的测量,那么在解模糊的过程中会得到错误的结果。
针对长短基线的物理基线长度难实现的问题,余数定理法可以较好地解决这个问题。但是因为其本身限制,基线长度之间必须互质,就会使得天线阵列形式受限,比较单一,而且在实际测向环境中往往噪声不可去除,因此余数的测量也是有偏差的,以至于最后入射角的测向结果存在误差。
3 虚拟基线法解模糊
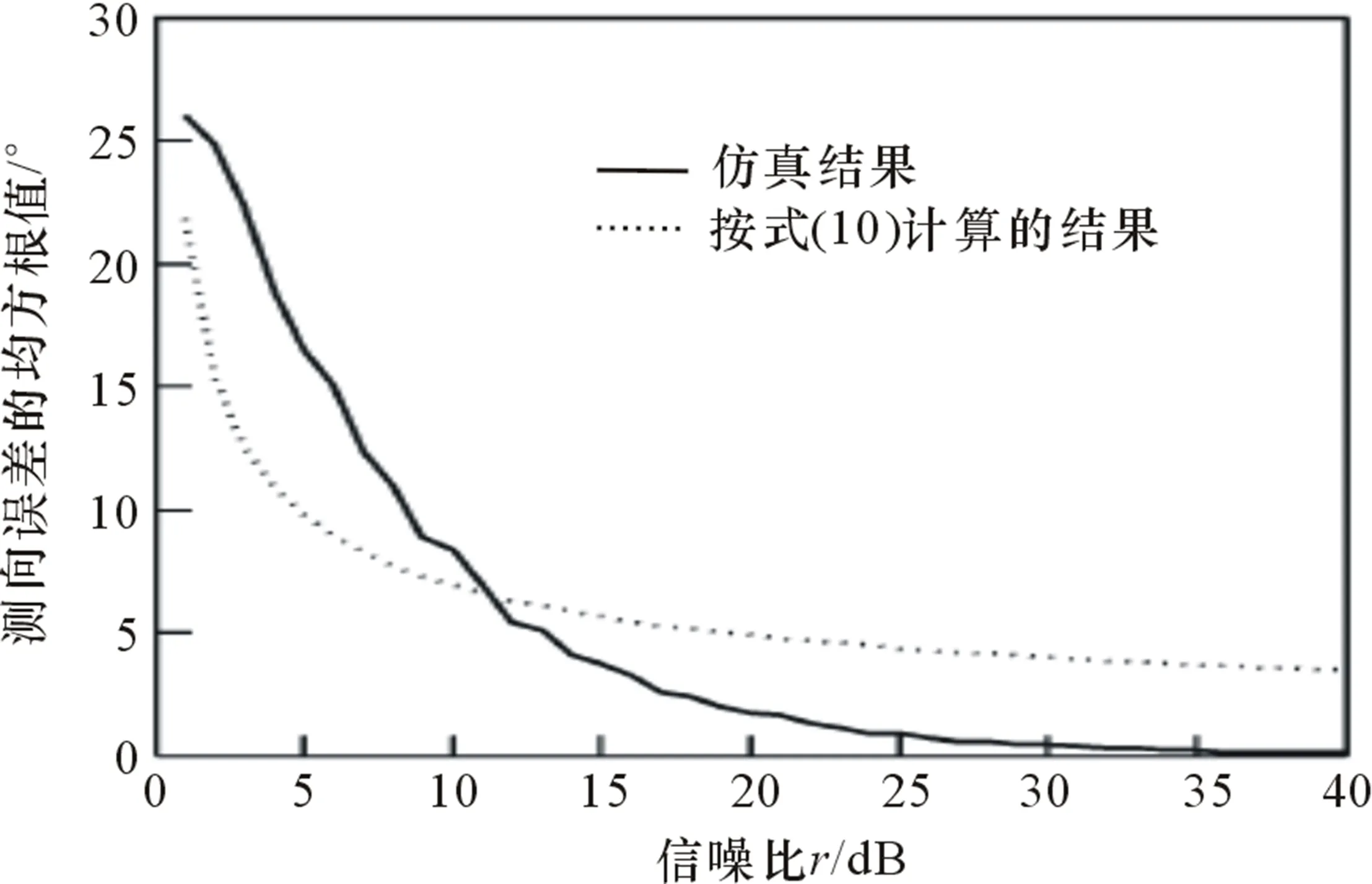
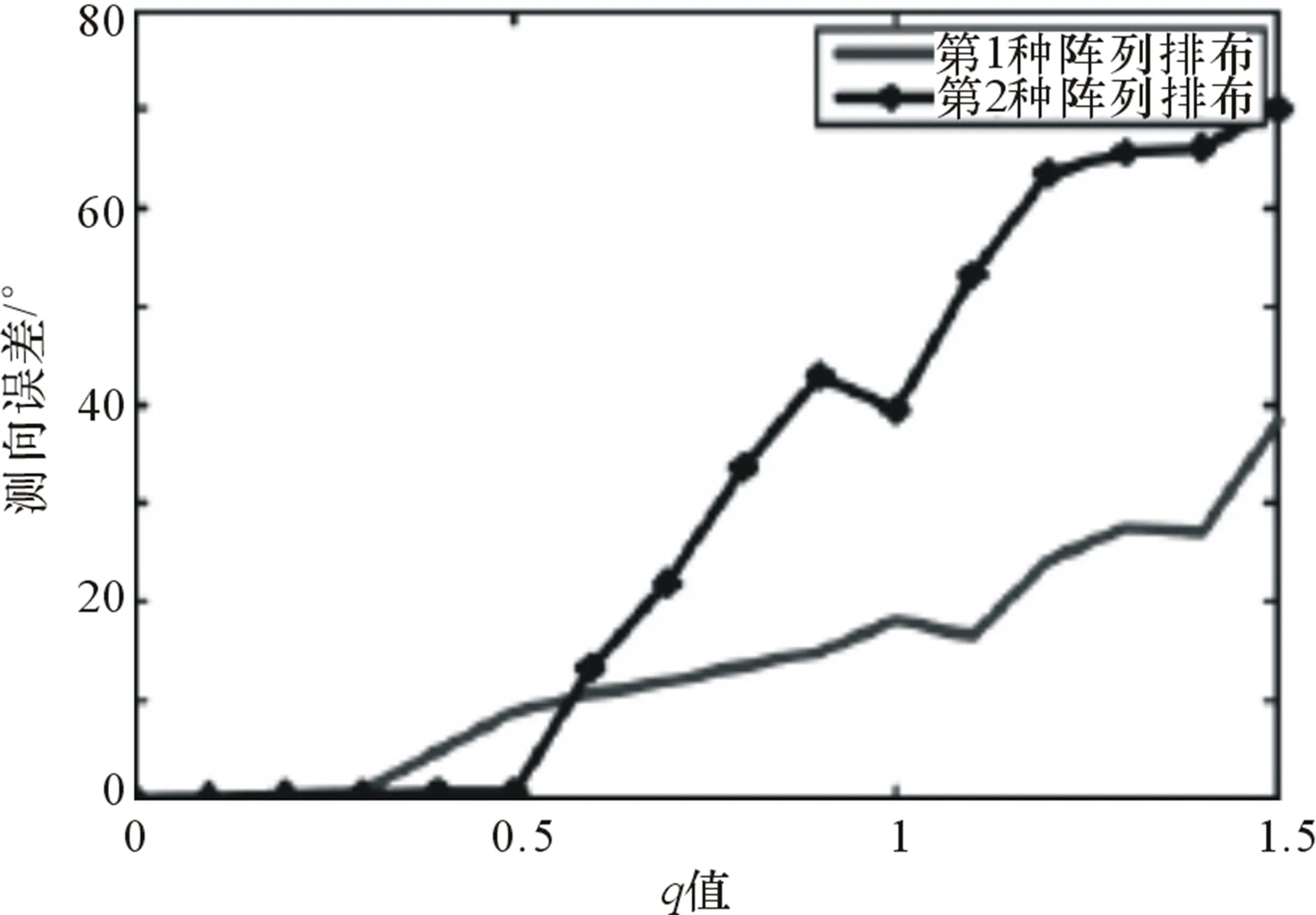
图4为一维n基线相位干涉仪天线阵示意图。设相邻基线长度分别为d1,d2,…,dn,且可以测得任意两天线i,j之间的相位差φij。构造的m条虚拟基线就是通过这n+1个天线得来,设为d1′=di1-dj1,d2′=di2-dj2,…,dm′=dim-djm,其中i1,i2,…,im,j1,j2,…jm∈[1,2,…,n]。设这m条基线满足一个关系:d1′ 图4 一维n基线相位干涉仪示意图 如图4所示,入射角为θ,那么两天线对应信号之间的相位差为: (6) 式中:φi为两天线之间的相位差,且φi∈[-π,π];Ni为整数;λ为入射信号的波长[6]。 因为入射信号频率已知,那么结合式(6)就可以测得θ: (7) 因为干涉仪单基线测向存在的模糊问题,Ni的值无法确定。长短基线法因为其缺点也不适用,因此这里通过构造虚拟基线法解模糊。式(6)代入不同的基线及结果φij,并相减,得到: (8) 式中:Nk′=Nik-Njk;φk′=φik-φjk;dk′=dik-djk,ik,jk∈[1,2,…,n]。 由图4,将基线长度表示为D1,D2,…,Dm+n,Di=di′,i=1,2,…,m为虚拟基线,Dm+j=dj,j=1,2,…,n,为实际基线,则有D1 (9) 式中:k=2,3,…,m+n。 其实该方法跟长短基线法还是有一些相同之处的,都是通过短基线来求解长基线的模糊,不同之处在于该方法通过构造虚拟基线法解决了物理天线长度过短无法实现的问题。 (10) 只要选取的基线长度符合解模糊时构造虚拟基线的条件,该方法可以很好地解决模糊问题。然而在实际工程测向中,因为很多误差因素会影响测向精度,因此在解模糊过程中往往采用逐级解模糊的方法,而不是直接用虚拟基线解模糊,那样产生的误差会比较大。而且,这种方法一般需要较多的天线阵元,对设备要求比较高,成本相对较高。 以双基线干涉仪测向系统为例,比较参差基线法和虚拟基线法的解模糊正确百分比:L=d1+d2=d12+d23=0.47 m,θ=-25°。 (a) 基于余数定理解模糊时,d12=0.36 m,d23=0.11 m; (b) 基于虚拟基线解模糊时,d1=0.24 m,d2=0.23 m。 当2种方法信噪比一样时,2种解模糊方法错误解模糊百分比(错误解模糊次数与总仿真次数之比,并用百分比表示)与信号波长间的关系曲线(4 000次独立仿真计算的统计结果)如图5所示。 图5 解模糊能力与信号波长之间的关系 通过虚拟基线解模糊时,也存在基线长度满足互质的情况,因此也对此种情况参与了比较,所以图5也给出了在满足(b)中基线条件时,采用余数定理解模糊的结果,记为余数定理解模糊1。 通过图5可以发现: (1) 当基线关系满足(b)中的条件时,虚拟基线法和余数定理法的解模糊能力基本一致,且不随着入射信号波长的变化而变化; (2) 当满足(a)中条件时,随着信号波长的增大,余数定理法的解模糊能力也会增强。 虚拟基线测向系统由3个天线组成,构成双基线测向系统。信号源频率为18 GHz,入射角为10°,信噪比为10 dB时,虚拟短基线测向误差的均方根值为σθ=6.9°。在不同信噪比条件下,进行了1 000次Monte-Carlo仿真实验,如图6所示。从图6可以看出,测向精度随着信噪比的增大而提高。 图6 测向误差与信噪比关系 图7 测向误差与信噪比关系图 通过仿真可以发现,在相同情况下,虚拟基线法的解模糊能力是逊于参差基线法的,在条件允许的情况下,选择参差基线法解模糊相对来说更好一些。 另外,当给定虚拟基线配置时,其解模糊能力是不会随着信号波长的增加而增强的。 本文针对相位模糊问题,提出参差基线法、虚拟基线法这2种工程上比较常用的解模糊方法,并分析其各自优缺点,通过仿真探讨影响测向精度的因素。同时通过比较这2种方法的解模糊能力,得出一定情况下,参差基线法的解模糊能力要优于虚拟基线法的结论,也给干涉仪测向系统解模糊方法的选择提供了依据。 [1] 毛虎,杨建波,刘鹏.干涉仪测向技术现状与发展研究[J].电子信息对抗技术,2010(6):1-6. [2] 罗贤欣,刘光斌,王忠.干涉仪测向技术研究[J].舰船电子工程,2012(8):74-76. [3] 任鹏,李建军,周彬,王建水.多基线干涉仪解模糊算法[J].电子信息对抗技术,2015(3):6-8. [4] 冯啸羽.干涉仪测向的校准技术研究[D].西安:西安电子科技大学,2012. [5] 司伟建.一种新的解模糊方法研究[J].制导与引信,2007(1):44-47. [6] 梁双港.基于相位干涉仪测向算法的定位技术研究[D].西安:西北工业大学,2006. Research into Interferometer Direction-finding Technology ZHAO Xiao-hua,LIANG Guang-zhen (The 723 Institute of CSIC,Yangzhou 225001,China) Interferometer direction-finding has the characteristics such as high direction-finding accuracy,high sensitivity,wide observation frequency band and so on,thus it is used widely in the electronic countermeasure,radar and other fields,but the weakness of phase interferometer is the linear range of the angle measurement is small.When the angle is bigger than the non-ambiguity view angle,the phase ambiguity may generate easily.Aiming at the problem of phase ambiguity,this paper puts forward two solving ambiguity methods of stagger baseline and virtual baseline,and compares the solving ambiguity capabilities through simulation experiments. interferometer direction-finding;solving ambiguity;stagger baseline method;virtual baseline method 2016-01-04 TN971.1 A CN32-1413(2016)03-0007-04 10.16426/j.cnki.jcdzdk.2016.03.002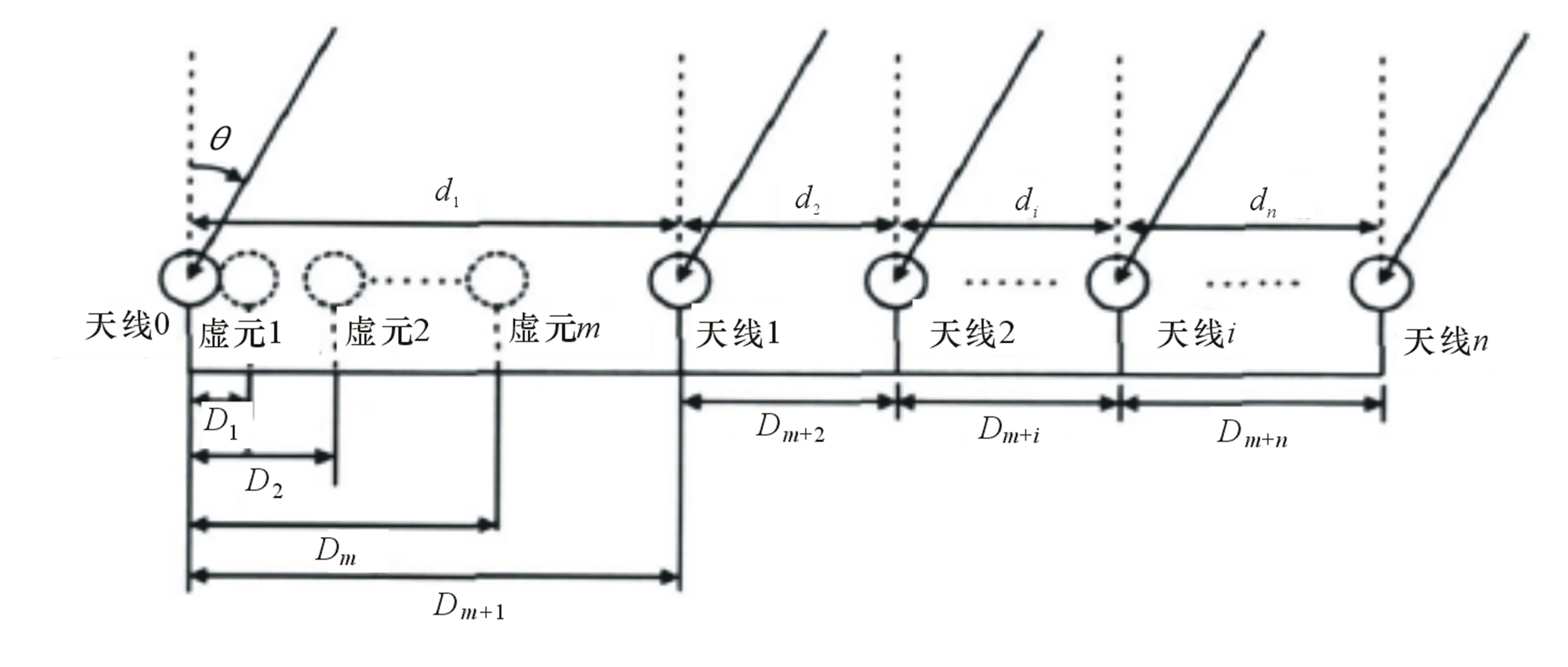
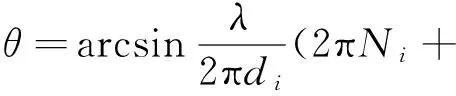
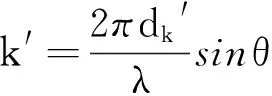
4 对比解模糊能力
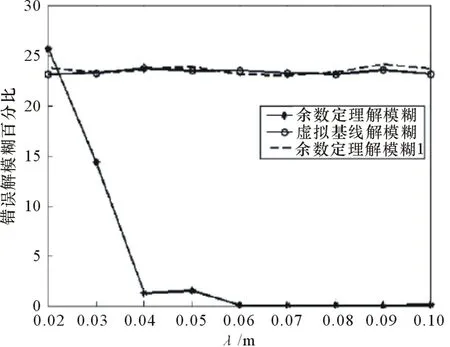
5 仿真实验
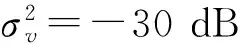
6 结束语

