初中数学教学中“顿悟”的策略与实践研究
刘绍洲

摘 要 我国的教育事业在不断改革和推进,在深化义务教育改革的过程中,注重对学生的素质教育培养,数学作为课程素质教育改革的重要学科,要注重学生在数学学习过程中的数学思维能力的培养,教师要在数学教学中不仅传授数学知识和数学概念、规律等,还要引导学生的数学学习思维,可以充分运用顿悟的方法,引导学生在数学思维过程中进行分析和思考,从而启迪学生的数学智力,提高学生的探究能力和创新精神。
关键词 初中数学 顿悟 数学思维
中图分类号:G424 文献标识码:A DOI:10.16400/j.cnki.kjdkz.2016.10.052
Abstract Education in our country in continuous reform and progress, in the process of deepening the reform of compulsory education, pay attention to students quality education and training, mathematical as an important subject of curriculum reform of quality education to pay attention to student learning in Mathematics in mathematical thinking ability in the process of training, teachers should not only teach mathematics knowledge and mathematics concepts, laws, should guide students in mathematics learning and thinking in Mathematics, can make full use of Epiphany, guide the students in mathematical thinking in the process of analysis and reflection, so as to inspire the students mathematical intelligence, improve students inquiry ability and innovation spirit.
Keywords junior high school mathematics; epiphany; mathematics thinking
初中数学的学习是一个复杂的过程,它体现了学生在数学学习过程中的直觉感知和逻辑思维。这两个思维过程是数学学习的前提和基础,同时也是数学学习顿悟的基础,它可以在数学学习过程中起到一个引导的作用,对学生的抽象逻辑思维能力和想象力都有较高的要求,在应用顿悟的过程中,可以使学生的数学认知架构不断由低到高,实现质的飞跃。
1 初中数学教学中顿悟的功用
数学教学中的顿悟是指在数学解题和知识教学的过程中,突然获得了解决数学问题的方法和思路,而这个方法和思路并不是凭空产生的,不是想象而来的,而是在特定的数学教学环境下因偶然的因素而造成的,也可以认为是创造性思维的数学教学内容,对学生的数学思维活跃性和开放性有重要的推动作用。顿悟在初中数学教学中的功用主要表现为以下几个方面:
(1)顿悟可以提升中学生对数学语言材料的理解和感悟。在初中数学的解题和知识学习过程中,汉语材料可以帮助学生进行理解和感悟。在一些数学解题过程中,有时不须严密的数学逻辑思维和推断,可以根据数学习题中的语言,分析数学问题,从而提升初中生对数学习题的读题速度,增强对数学语言材料的感悟能力。
(2)顿悟可以提升学生数学学习的主动性和开放性。在数学学习活动中,学生的参与程度,在较大程度上影响了数学知识的学习效能,传统的数学教学注重数学概念和规律的传授,而对学生数学思维的培育较少,而顿悟可以让学生的主动性合理地调动,并且可以在一定程度上活跃数学课堂氛围,增强学生主动思维的能力,提升数学学习效果。
(3)顿悟有助于学生创新思维能力的培育。初中数学教学不仅要传授数学知识,还要培养学生的数学创新思维能力,运用顿悟式教学方法,可以让学生进行手脑并用的思考和分析问题,在不经意间产生顿悟,培育出学生的创新思维能力。
2 初中数学教学中顿悟的开放性研究及探索
2.1 注重学生在数学情境中进行多层次的数学解答
在初中数学的知识学习过程中,学生要具有良好的数学知识结构,要具备足够灵活的双向产生式知识和层次分明的解题意识,在条件前提和数学结构的知识储备之下,进行多层次、多角度的数学问题解答和探索。在运用顿悟的数学教学过程中,实现多层次的数学问题解答,需要从以下几个方面加以考虑:
2.1.1 要注重数学知识的触发条件
数学概念和数学定理可以用于解决相应的数学问题,然而,这些数学概念和数学定理在情景条件发生变化的情况下,学生不会灵活地运用数学概念和定理。这就需要考虑数学知识产生的触发条件,在多层次的知识产生链的结果之下,要注重每一个知识点的触发条件,要建立数学知识和数学问题之间的丰富联结,并将数学知识镶嵌在具体的数学问题情境之中,试探学生在数学问题情境之中对条件信息的识别状态,并由此引发的数学学习活动。
例如:在对已知条件得知三角形是直角三角形的识别产生条件下,学生可以作出反应,并判定:斜边的平方等于两条直角边的平方之和,在这个勾股定理的检索信息之中,学生还没有将其具体应用于数学问题情境,还需要溶入个体数学活动的体验,并在数学问题信息提取、分析和整理的过程中,实现知识的迁移。
2.1.2 要建构数学知识的组块体系
在运用顿悟策略和方法的数学学习过程中,要将学生长时记忆的数学知识储存在有序的认知结构之中,在对数学问题进行分析的过程中,要从不同角度对数学概念和数学命题进行梳理,在逐步完善数学认知结构的条件下,形成数学知识组块体系,为多角度、多层次的数学问题解答提供条件和前提。
2.1.3 探索开放性数学问题情境之中的多层次解答
在数学顿悟教学的方法之中,要以探索为数学教学的生命线,在开放性的答案解答过程中,对问题进行验证和修正,使学生在探究性的数学研究过程中进行多层次的解答,体验如何“做数学”,并实现对数学问题的“再创造”。
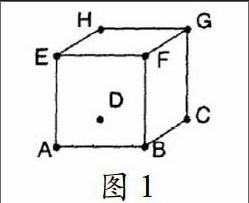
例如:有一个边长为a的正方体ABCD-EFGH(图1),在底部的A处有一只猫,在A的对角顶点处有一只老鼠,猫可以沿着什么路线前进,可以在最短的时间内抓住老鼠(假设前提条件为老鼠在G处不动),试画出有多少条路径?
习题解答:教师可以启发学生将这个问题进行转化,设计成由A-G处的最短路径问题,学生思考后对这个问题进行解答:在A和G处的两点之间的连线最短,它们之间连线的路径可以进行计算得知。
T:这条路径虽然最短,然而,我们的前提条件是猫不会飞,这条路径事实上并不存在。
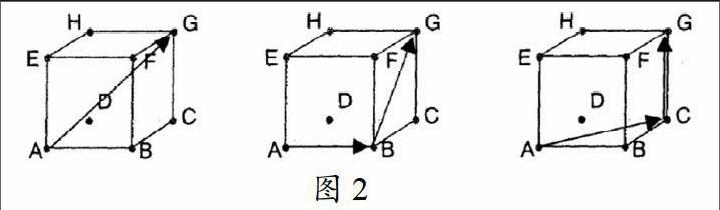
S:可以沿着正方体的对角线和棱边往前行,有A-B-G,A-E-G,A-D-G……将其进行路径的计算可以得出最短路线。如图2所示:
T:为了启发学生的数学领悟能力,教师可以对学生进行启发:沿着正方体面比沿着棱进行前行的距离更短,学生请思考,还有什么更佳的选择?
S:(停顿、领悟并思考)
T:让学生预备好正方体纸盒,做好相应的字母标注,观察并交流,当学生在正方体上画线或者将正方体纸盒沿底面展开之时,学生获得了顿悟:原来将正方体沿底面展开,可以使解题思路变得豁然开朗。
S:从A处到G处的路径,明显在平面上可以看出AG的路径小于A-C-G的路径,也即由A到CD的中点再到G点是最短的路径。
T:由此可以进行规律性的总结:由A处—G处的路径在以A和G为顶点的两个正方形的表面上且经过这两个相邻正方形的公共边的中点。
2.2 注重初中数学思想和方法在学习中的运用,激发学生的顿悟
数学思想和方法是重要的教学内容,它可以激发学生的数学学习兴趣,领悟到这些关键数学思想的实践应用,并在独立自主思考的前提下,进行新知的探究和发现、分析,从而创造性地解决数学问题。为了正确地运用好数学思想和方法在实践解题中的应用,要遵循学生的认识规律,分层次地渗透归纳和演绎等数学学习方法,使学生形成良好的数学思维习惯,培养学生自我提炼、揣摩和概括数学思想和方法的能力。
2.2.1 分类思想在数学教学中的实践运用
初中数学分类思想渗透于数学概念性的内容以及数学证明题和计算题中,它在代数和几何的教学中,可以极大地提升学生的条理性思维和数学逻辑思维。从几何角度而言,分类思想可以运用于比较线段的大小问题。
例如:在两条线段之中,可以讨论并比较线段AB和CD的大小。运用分类思想,进行三种不同情况的分类讨论:(1)当点B在CD线段之上时,AB
2.2.2 数形结合思想在数学教学中的实践运用
在初中数学解题过程中,通常运用数与形的结合,在“以形助数”和“以数解形”的过程中,可以使复杂的数学问题简单化、抽象的问题直观化,分析数学问题的题设和结论之间的关联,从而快速解决数学问题。它对培养学生的图形感和数感有极大的辅助作用,并在学生的形象思维和抽象思维的综合利用方面,有一定的促进作用。
例如:“空间与图形”中的数形结合。如图3,有一根12m长的铁丝,围成一个矩形空地,如何才能使围成的面积最大?围出面积的长宽度如何?
解题思路:要从“最多”的条件中进行数学思维的启发,引导学生进行顿悟,结合二次函数,以面积为等量关系,解决这道最值问题,在数形结合的解答过程中,培养数学解题思维。
即:当面积的长为3,宽为6时,面积最大,透光最多。
2.2.3 函数与方程思想在数学教学中的实践运用
函数与方程是初中数学教学中的重要内容,对学生的数学解题思维具有深远的影响,它在探索、归纳、提炼的解题过程中,运用数学思想和方法,在掌握这些数学思想的特性的前提下,进行反复的渗透和训练,在适当的引进策略下,引导学生进行知识的顿悟和体会,从而对数学知识进行反思、提炼和归纳。
解题思路2:运用数学函数的知识点,要让学生在方程向函数转化的顿悟之中,借助于两者之间的关系,发现求方程 + = 0的解也即二次函数 = + 的图像与轴的交点,同时,由于抛物线开口向上,因而只要满足 = 1时,<0即可,即 + <0,得<2。
2.3 从学生的直觉思维角度,激发数学学习中的顿悟
数学顿悟的产生需要学生的知识储备前提和良好的数学认知结构前提,在此条件之下,教师才能引导学生进行想象、联想、发散和求异,从而产生数学顿悟。在初中生的思维结构和认知水平之中,可以首先从学生的直觉思维角度,进行顿悟的激发,培养学生的数学知识理解能力和运用能力。
例如:如图4,已知在 ABC之中,AD、BE、CF分别是BC、AC、AB边上的中线,G是重心,AG = 6,BG = 8,CG = 10,试求 ABC的面积为多少?
教师在教学过程中,可以利用学生的直觉思维,明白这个习题中的实质即:三个数据6、8、10也正是勾股数,在这个直觉思维的导向之下,使学生产生顿悟,获得解题思维的训练和强化,以6、8、10为长的三线段构造一个直角三角形,延长线段GD至G,并使GD=GD,连结GC,这样可以较为容易地获得证明:GG=AG=6, GDB≌ GDC,由此可得,GC=BG=C, GGC是直角三角形, GGC的面积为6€?€?=24, ABC的面积为72。
2.4 从学生的逻辑思维角度,激发数学学习中的顿悟
在数学思维的产生过程中,学生的逻辑思维较直觉思维而言,具有更高、更为复杂的层次,为了揭示数学知识的本质特征和规律性联系,可以引导学生在逻辑思维的构建中,产生数学顿悟,提升数学思维能力和解题能力。
例如:请解析下列方程组:
解题思路1:方程①去分母,再采用代入消元法,进行解题,显然这是一种较为繁琐的解题方法。
解题思路2:两个方程的左边系数相同,因而可以考虑将+(9/)和+(4/)视同为一个整体,将方程②的左右两边都除以,并把方程②变形为(+9/)(+4/)=24,然后再将方程①变形为(+9/)+(+4/)=10,假设+9为A,+4/为B,这样,方程组就可以转化为A+B=10,A€譈=24,后续的解方程组就变得容易许多了。
在上述的数学解题过程中,对“两个方程的左边系数相同”的敏感思维也即顿悟过程,在强化逻辑训练的过程中,激发学生的顿悟,提升数学解题能力。
2.5 充分挖掘学生的猜想和联想能力,拓展数学学习的顿悟
在数学的顿悟产生过程中,要经历一个初步认识—逐步提高—进一步深化的过程,也即数学猜想和联想的过程,由数学条件或结论的外表猜想到内在的定理或图形,从而获得顿悟,寻找到解题灵感。
例如:有一条流水线上的N台机床在工作,要设计一个零件供应站点P,为了使N台机床与零件供应站点P之间的距离总和最小,可以将P点设置于何处?
解题思路:在这个解题过程中,由于N是一个抽象值,要引导学生获取具体值,就需要引导学生对正确的解法进行猜想和假设:
当N=2时,P点应位于何处呢?当N=3时,P点又位于何处?N=4,N=5呢?
在引导学生进行归纳的同时,可以得到怎样的猜想?
当N为奇数时,P点在第(N+1)/2台处时,距离之和最小。
当N为偶数时,P点在第N/2和(N/2+1)台之间的任何一点时,距离之和最小。
3 结束语
在初中数学教学中,要培养学生独立自主思维的能力,要结合学生的形象思维和抽象逻辑思维,运用数学思想和数学方法,进行数学问题的主动探索和创新,在对数学问题进行知识分析、推理和归纳、概括的过程中,启发学生的顿悟,从多角度对数学问题进行探索,可以培养学生在数学思维中的灵活性、独立性,增加对数学解题的深度和广度,运用顿悟教学的原则,全面提升数学学习能力。
参考文献
[1] 张彬.提升学生数学迁移能力的教学策略探析[J].数学教学通讯,2016(12).
[2] 余飞.农村初中数学课堂提问的策略探析[J].语数外学习(初中版中旬),2014(11).
[3] 丘立峰.课堂组织艺术在数学课堂教学中的渗透[J].现代阅读(教育版),2013(3).
[4] 江翠玲.如何用情景教学培养学生的创造性思维能力[J].河南农业,2010(2).
[5] 吴泽华.忽如一夜春风来 千树万树梨花开——浅议初中数学教学中的顿悟[J].数学教学通讯,2013(10).

