核实数据下非线性模型的序列相关性检验

刘 锋，何 卓,谭祥勇

(重庆理工大学 数学与统计学院，重庆 400054)



核实数据下非线性模型的序列相关性检验

刘 锋，何 卓,谭祥勇

(重庆理工大学 数学与统计学院，重庆 400054)

研究了核实数据下非线性模型的序列相关检验问题,并运用经验似然的方法构造了检验统计量，证明了该检验统计量在零假设下的渐近分布。数值模拟结果显示：提出的检验效果比较理想。

核实数据；非线性模型；序列相关性检验；经验似然

考虑如下非线性模型：

Y=f(X,β)+ε

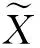
检验一个模型的残差是否存在相关性是一项非常重要的工作,若模型的残差存在序列相关性，则作出的相关统计推断将会失去有效性。对于序列相关性问题的研究见文献[5-6]。关于核实数据下非线性模型的序列相关研究还比较少。本文研究了核实数据下非线性模型的序列相关检验的问题。本文主要利用经验似然的方法来构造检验统计量。关于经验似然更多的技术见文献[7-10]。

1 方法和主要结果

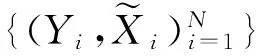
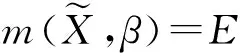
(1)

这样，对εi进行序列相关检验相当于对ei进行序列相关检验。假设εi具有p阶序列相关，则ei也具有p阶序列相关。

令uk=E(eiei+k),U=(u1,u2,…,up)，k=0,1,…,p。由文献[5]可知：零假设和备择假设分别为

H0:U=0v.s.H1:U≠0

令zi1=eiei+1,zi2=eiei+2,zip=eiei+p，且记

Zi=(zi1,zi2,…,zip)Τ,i=1,2,…,N-p

则在零假设下有E(Zi)=0,i=1,2,…,N-p，因此问题就转换成检验E(Zi)=0。

由文献[10]可知：可以利用经验似然的思想来检验E(Zi)是否为0。

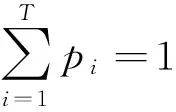
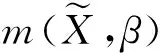
(2)

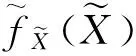
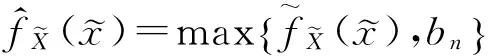
(3)

对于参数β的估计,在零假设和主要数据下，利用最小二乘的方法可得

(4)

(5)

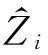
(6)

由Lagrange乘数法求得满足式(6)的pi由式(7)给出。

(7)

其中λ是方程(8)的解。

(8)

将式(7)代入式(6)可得

(9)

令c为不同地方取不同值的正常数。对任意向量a，用‖a‖表示Euclidean模。设Dm是Rd(m>d+1)或其子区域上所有连续函数q(·)组成的类，使0≤i1+i2+…+id≤m,偏导数

一致有界。

下面的定理需要满足以上条件:

C1：E‖X‖2<∞；

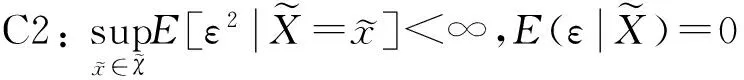
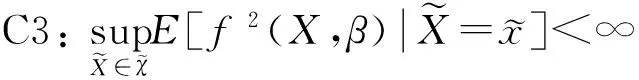
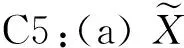
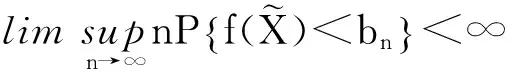
C6：K(·)是非负有界的m阶核函数，且具有有界支撑，其中m同C4中的定义；

C8：N/n→γ，其中γ≥0为常数。

以上条件的合理性见文献[4]。

由定理1可知：在给定的显著性水平α下，当对数经验似然比的值大于渐进分布的1-α分位数时，则拒绝零假设,即认为残差存在序列相关性。

2 模拟结果

为简单起见，假设如下模型：

(10)

其中：Xi～U(0,1)；η～N(0，0.16)。对于任意εi，满足下面4个模型：

模型AR(1):εi=ρεi-1+ξi,|ρ|<1;

模型MA(1):εi=ρξi-1+ξi,|ρ|<1;

模型AR(2):εi=a1εi-1+a2εi-2+ξi;

模型MA(2):εi=a1ξi-1+a2ξi-2+ξi;

其中ξi～N(0,0.4)。

假设核实数据和主要数据分别为(n,N)=(20,100),(50，100),(40，200),(100，200),(60，300),(150，300)。 对于每组样本量情况,取显著性水平为0.05,各做2 000次模拟,结果见表1-4。

由表1～4可以看出：不论误差服从何种模型，在零假设下，随着样本量的增加，检验的水平迅速收敛到给定的显著性水平0.05；在备择假设下，不管误差序列是AR模型还是MA模型，经验似然比检验的功效都表现得非常好；同时，随着核实样本量的增加,似然比检验的水平和功效表现得越来越好。

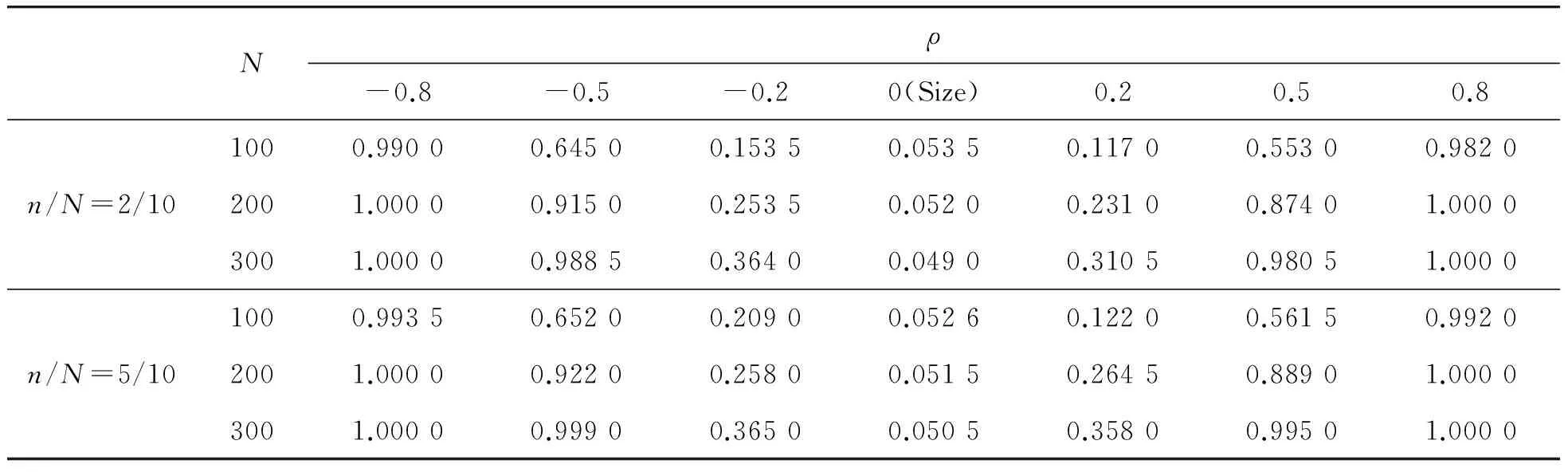
表1 经验似然比检验，误差服从AR(1)模型

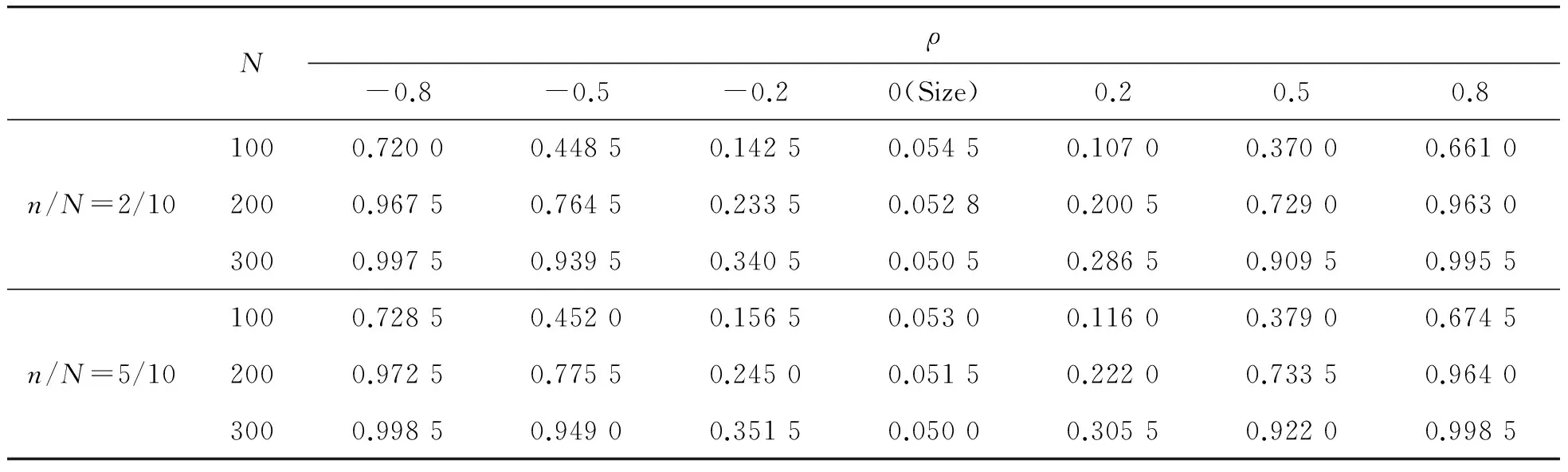
表2 经验似然比检验，误差服从MA(1)模型

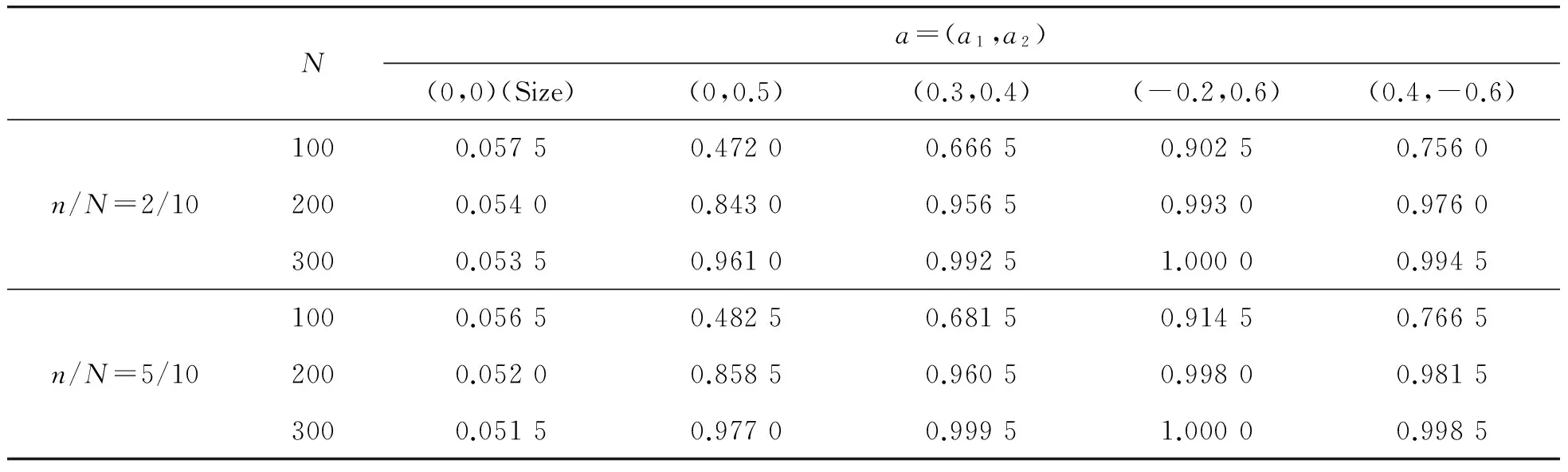
表3 经验似然比检验，误差服从AR(2)模型

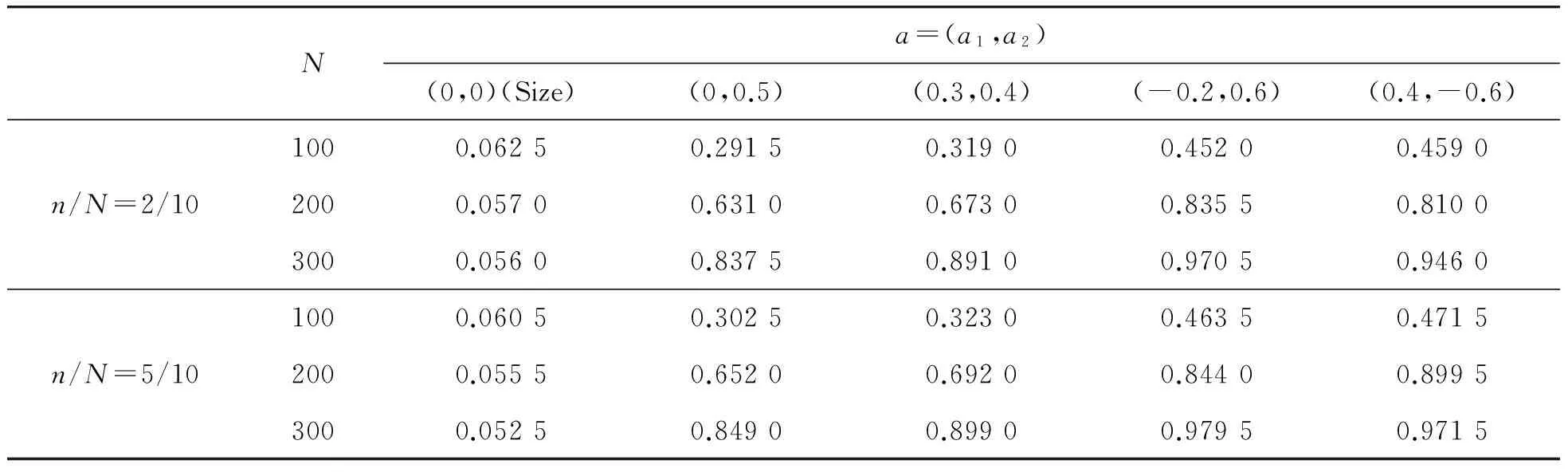
表4 经验似然比检验，误差服从MA(2)模型

3 定理的证明

由于T=n-p，根据条件C8，在本文中不区分Op(n)和Op(T)。

引理1 在零假设和条件C1～C8下，有

证明 见文献[4]的定理2.3。

引理2 在零假设和条件C1～C8下，i=1,2,…,N,有

(11)

和

(12)

证明 式(11)的证明见文献[4]的引理4.1。下面证明式(12)。

由引理1和式(11)易得式(12)成立。

引理3 在零假设和条件C1～C8下，有：

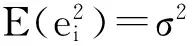
证明 对任意的整数k(1≤k≤p),有

其中：

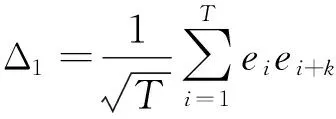
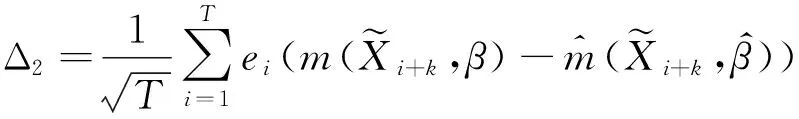
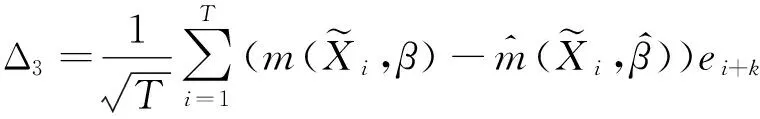
对于Δ2,利用引理2,易得

且EΔ2=0,所以Δ2=op(1)。

同理可得Δ2=Δ3=op(1)。

对于Δ4有

且E(Δ4)→0,故Δ4=op(1)。

因此，可以得到

令α是任意p维非零向量，αΤZi是在零假设下的独立随机变量序列,则

Cov(αTZi,αTZj)=αTCov(Zi,Zj)α=0，i≠j

由m步相依随机变量中心极限定理[11]，可得

其中Z=ααΤσ4。然后运用Cramer-Wold方法，能够推导引理3。

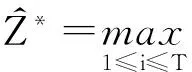
证明 引理4的证明与引理3类似，故略去证明。

引理5λ是拉格朗日乘子，有

‖λ‖=Op(T-1/2)

证明 证明类似于文献[10]中的引理3。

定理1的证明

对(8)的泰勒展开和引理4～5，能得到

通过简单的计算和根据引理3～5，有

通过引理3和引理5可知定理1成立。

4 结束语

因时间、花费等原因,只能得到一部分精确的观测值,取而代之的是得到具有观测误差的替代值。目前，对于核实数据的研究主要是对相关的参数进行统计分析,但对于序列相关性的检验研究得还较少。因此，本文研究了核实数据下非线性模型的序列相关检验,采用了经验似然的方法构造了检验统计量,并证明了其渐进分布。通过数值模拟验证了本文所提出的检验统计量的有效性。

[1] PEPE M S.Inference using surrogate outcome data and a validation sample[J].Biometrika,1992,79(2):355-365.

[2] SEPANSKI J H,LEE L.Semiparametric estimation of nonlinear errors-in-variables models with validation study[J].Journaltitle of Nonparametric Statistics,1995,4(4):365-394.

[3] WANG Q.Estimation of partial linear error-in-variables models with validation data[J].Journal of Multivariate Analysis,1999,69(1):30-64.

[4] 薛留根.核实数据下非线性半参数 EV 模型的经验似然推断[J].数学学报,2006,49(1):145-154.

[5] 刘锋,陈敏,邹捷中.部分线性模型序列相关的经验似然比检验[J].应用数学学报,2006,29(4):577-586.

[6] HU X,LIU F,WANG Z.Testing serial correlation in semiparametric varying coefficient partially linear errors-in-variables model[J].Journal of Systems Science and Complexity,2009,22(3):483-494.

[7] OWEN A B.Empirical likelihood ratio confidence intervals for a single functional[J].Biometrika,1988,75(2):237-249.

[8] OWEN A B.Empirical likelihood ratio confidence regions[J].The Annals of Statistics,1990,18:90-120.

[9] OWEN A B.Empirical likelihood[M].State of Florida:CRC press,2001.

[10]OWEN A B.Empirical likelihood for linear models[J].The Annals of Statistics,1991:1725-1747.

[11]BROCKWELL P J,DAVIS R A.Time series:theory and methods[M].New York:Springer Science & Business Media,2013.

(责任编辑 陈 艳)

Testing for Serial Correlation in Nonlinear Model with Validation Data

LIU Feng, HE Zhuo, TAN Xiang-yong

(College of Mathematics and Statistics, Chongqing University of Technology,Chongqing 400054, China)

This paper considers the serial correlation testing for nonlinear model with validation data,and uses the empirical likelihood method to establish the testing statistic,and justifies the asymptotic distribution of the statistic. Simulation results indicate that the testing statistic performs well both size and power.

validation data; nonlinear model; serial correlation test；empirical likelihood

2016-06-18 基金项目：国家自然科学基金资助项目(11471060)；重庆理工大学研究生创新基金资助项目(YCX2014234)

刘锋(1973—)，男，湖南新化人，博士，副教授，主要从事非参数统计研究,E-mail:fliu@cqut.edu.cn。

刘锋，何卓,谭祥勇.核实数据下非线性模型的序列相关性检验[J].重庆理工大学学报(自然科学)，2016(11):155-161.

format：LIU Feng, HE Zhuo，TAN Xiang-yong.Testing for Serial Correlation in Nonlinear Model with Validation Data[J].Journal of Chongqing University of Technology(Natural Science)，2016(11):155-161.

10.3969/j.issn.1674-8425(z).2016.11.025

O212

A

1674-8425(2016)11-0155-07