基于分层Copula理论的股市联动性测度
罗 燕,吴 永
(重庆理工大学 数学与统计学院,重庆 400054)
基于分层Copula理论的股市联动性测度
罗 燕,吴 永
(重庆理工大学 数学与统计学院,重庆 400054)
在ARMA-EGARCH模型下,考虑好坏消息对股市的不对称性影响,根据分层阿基米德Copula的灵活性与有效性,分析美国与亚太地区6只股指联动性;进一步通过CoVaR度量股市间系统性风险溢出效应,与分层阿基米德Copula的分层结构较一致。新加坡与香港联动性最强,台湾与日经次之,表明联动关系的强弱与系统性风险溢出效应相关联。
分层阿基米德Copula;CoVaR;ARMA-EGARCH
现代金融体系主要以网络化呈现,金融机构彼此相互关联、相互影响。一些金融机构自身规模及业务复杂且相互关联,对整个金融系统持有较大地负外部冲击。早期Adrian等[1-2]提出系统性风险条件在险价值(CoVaR)。基于Copula函数的灵活性,Karimalis 等[3]运用Copula函数分析欧洲银行业间关系,并进一步预估其CoVaR。沈悦等[4]通过构建GARCH-Copula-CoVaR模型,度量金融体系中保险、证券、信托及银行对整个系统性风险的贡献度和各市场间的风险溢出度。考虑分层条件Copula函数,结合经典ARMA-GARCH模型,杜子平等[5]对英美以及亚太地区部分股市股指进行相关性分析。张连增等[6]利用两步参数法构造分层阿基米德Copula,对国内股票收益率进行时间序列相关性分析。
本文在ARMA-EGARCH模型下,考虑好坏消息对股市的不对称性影响,根据分层阿基米德Copula函数的灵活性与有效性,初步考虑股指分层结构作为关联强弱的判断依据,并进一步通过CoVaR度量分析股市间系统性风险的溢出效应。
1 分层Copula理论
1.1 Copula
定理1[7-8]令随机变量X=(X1,…,Xd)′~F,Xj~Fj,j=1,…,d,那么存在一个d维CopulaC,使得式(1)成立,即:
(F(x)=C(F1(x1),…,Fd(xd)),
x∶=(x1,…,xd)′∈(R∪{-∞,∞})d)
(1)
1.2 Archimedean Copula
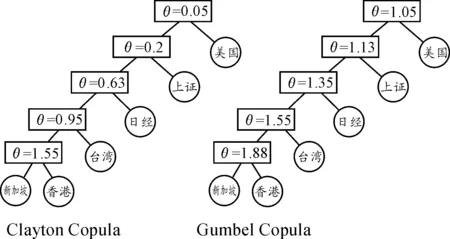
d维阿基米德Copula(Archimedean Copula,AC)所有k维(k 定义3[9]d维CopulaC称为AC,如果C可以表示为式(2),则有 C(u1,…,ud)=φ(φ-1(u1)+…+ φ-1(ud)),(u1,…,ud)′∈[0,1]d (2) 其中φ∈Ψ,φ的逆函数φ-1∶[0,1]→[0,∞]满足φ-1(s)=inf{t∶φ(t)=s},s∈[0,1]。 1.3 分层阿基米德Copula 分层阿基米德Copula(Hierarchical Archimedean Copula,HAC)为嵌套阿基米德Copula(nested Archimedean Copula),包括完全嵌套(fully-nested Archimedean Copula,FNAC)和部分嵌套(partially-nested Archimedean Copula,PNAC)。分层处理时维数呈缩减状态,能对变量间不同相依结构进行有效测度。 定义4[7-8]对任意d维(d≥2)CopulaC,若C可以表示为: (3) 2.1 样本选择与预处理 2.1.1 描述性统计 用FNAC分析美国与亚太地区6只股票指数:新加坡海峡时报、日经225、上证、道琼斯工业平均、台湾加权、香港恒生,依次用series1~6表示。考虑2007—2009年金融危机影响,选取2005-01-01至2016-04-11日交易收盘价,数据来源于锐思数据库,整合样本后共获取2 405个交易数据,实证研究结果由R实现。 为充分体现指数波动性,采用对数一阶差分形式,即Ri,t=100(lnPi,t-lnPi,t-1),Pi,t表示第i个指数t期收盘价,i=1,…,6,t=2,…,2 405。图1给出了{Pi,t}与{Ri,t}趋势,表1给出了{Ri,t}描述性统计特征。series1,4~6指数价格变化具有较明显趋同性,series2~3略有不同;收益率的波动表明指数之间可能存在相关性。 如表1所示,峰度比3大,偏度为负(新加坡除外),说明{Ri,t}具有厚尾、左偏等特性。Jarque-bera统计量及其p值表明{Ri,t}不服从正态分布。 图1 {Pi,t}与{Ri,t}趋势表1 {Ri,t}描述性统计特征 样本新加坡日经上证道琼斯台湾香港均值0.0127330.0130210.0371270.0208680.0143770.015607标准差1.3998521.6941641.9331351.2501641.3294761.695549偏度0.370570-0.739547-0.550517-0.378120-0.399830-0.174680峰度20.3429169.2061084.37256510.9738095.33908912.242344最小值-11.478201-12.111026-14.168079-11.269800-9.189815-15.971979最大值15.47188913.2345859.03425110.3259189.24302013.406809Jarque-bera统计量415878727.52042.1121452926.915056p值000000 2.2 边际分布估计 2.2.1 ARMA-EGARCH模型 时间序列{Rt}服从ARMA-EGARCH模型,如果Rt满足: φiRt-i+ (4) εt=σtμt (5) (6) 综合AIC、BIC及模型待估参数个数,分别用t、GED、偏t及偏GED拟合分布,并进行序列概率积分转换,运用K-S检验选取最优边际分布,结果如表2所示。 2.3 FNAC参数估计及模型选择 根据ARMA-EGARCH模型参数估计结果,运用极大似然法,两两分层比较。如图2所示,Clayton与Gumbel Copula分层结构一致,香港与新加坡联动性最强,台湾与日经次之,与图1价格趋势分析结果一致。比较极大似然值表明:Clayton优于Gumbel Copula估计结果。 图2 FNAC结构 2.4 基于分位数回归法的CoVaR值 (7) (8) (9) 受地域影响,新加坡、上证、日经、台湾和香港相互间溢出效应明显强于与道琼斯间的溢出效应。与FNAC结果较为一致,表明联动关系的强弱与系统性风险溢出效应相关联。 表2 ARMA-EGARCH模型估计结果 表分析结果 表分析结果 本文考虑股指间的好坏消息的不对称性影响以及Archimedean Copula可交换的局限性,引入分层阿基米德Copula,并进一步通过CoVaR度量股市间系统性风险溢出效应。结果表明:新加坡、上证、日经、台湾和香港相互间溢出效应明显强于与道琼斯间的溢出效应,联动关系的强弱与系统性风险溢出效应相关联。 [1] ADRIAN T,SHIN H S.Financial intermediary leverage and value at risk[R].New York:Federal Reserve Bank of New York Staff Reports,2008:338. [2] ADRIAN T,BRUNNERMEIER M K.CoVaR[R].[S.l.]:National Bureau of Economic Research.2011:17454. [3] KARIMALIS E N,NOMIKOS N.Measuring systemic risk in the European banking sector:A Copula CoVaR approach[R].London:Working paper,Cass City College,2014. [4] 沈悦,戴士伟,罗希.中国金融业系统性风险溢出效应测度——基于 GARCH-Copula-CoVaR 模型的研究[J].当代经济科学,2014,36(6):30-38. [5] 杜子平,高立宝.国际股票市场金融危机传染路径实证分析[J].商业时代,2013 (13):55-57. [6] 张连增,胡祥.基于分层阿基米德Copula的金融时间序列的相关性分析[J].统计与信息论坛,2014,(06):34-40. [7] BRECHMANN E C.Hierarchical Kendall Copulas and the Modeling of Systemic and Operational Risk[D].Munich:Universitätsbibliothek der TU München,2013. [8] OKHRIN O,RISTIG A,SHEEN J,et al.Conditional Systemic Risk with Penalized Copula[R].Berlin:Humboldt University,2015. [10]史代敏,谢小燕.应用时间序列分析[M].北京:高等教育出版社,2011. (责任编辑 陈 艳) The Stock Market Linkage Measurement Based on Hierarchical Archimedean Copula Theory LUO Yan, WU Yong (College of Mathematics and Statistics, Chongqing University of Technology,Chongqing 400054, China) Considering the impact of the asymmetry index between good and bad news under ARMA-EGARCH model, this paper analyzes index linkageof 6 stocks in the US and Asia-Pacific area with the Hierarchical Archimedean Copula. Furtherly, systemic risk spillover effect between stock market are measured by CoVaR, and the result is consistent with the hierarchical structure of the Hierarchical Archimedean Copula: linkage of Hong Kong and Singapore stock market is the strongest, followed by Taiwan and Rijing. It shows that the strength of the relationship and systemic risk spillover effect are related. Hierarchical Archimedean Copula; CoVaR; ARMA-EGARCH 2016-05-23 基金项目:国家社会科学基金资助项目(14BJY200) 罗燕(1990—),女,重庆巫山人,硕士研究生,主要从事复杂系统模型与仿真研究,E-mail:353151641@qq.com。 罗燕,吴永.基于分层Copula理论的股市联动性测度[J].重庆理工大学学报(自然科学),2016(11):171-176. format:LUO Yan, WU Yong.The Stock Market Linkage Measurement Based on Hierarchical Archimedean Copula Theory[J].Journal of Chongqing University of Technology(Natural Science),2016(11):171-176. 10.3969/j.issn.1674-8425(z).2016.11.028 F224.0;O212.1 A 1674-8425(2016)11-0171-06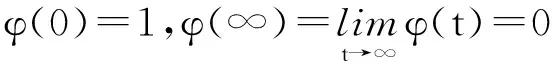
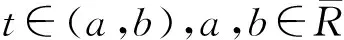

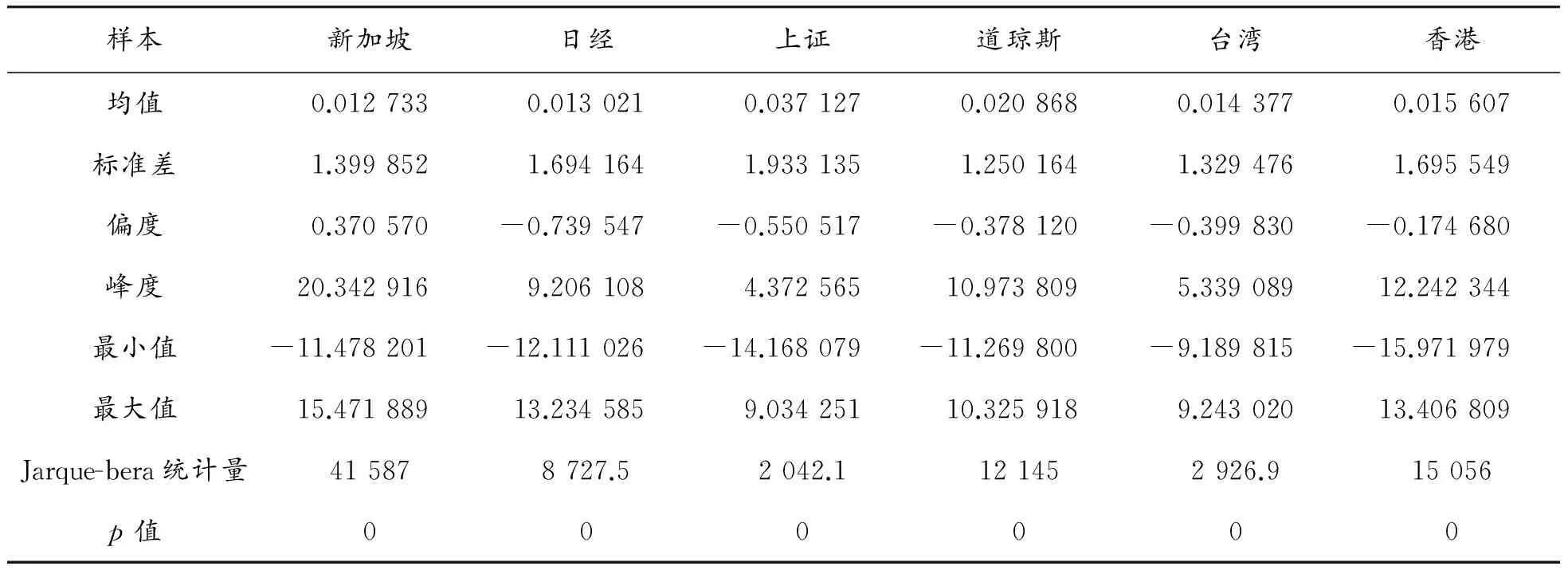
2 实证研究


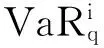
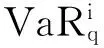

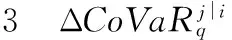

3 结束语

